Facciamo un passo indietro e torniamo al nostro spazio normale descrivibile attraverso i punti che abbiano coordinate x,y,z in un sistema cartesiano ortogonale. Per rimanere in una situazione simile a quella del diagramma di Minkowski, riduciamolo a un piano di coordinate x e y (insomma, spostiamoci su Flatlandia). In questo piano consideriamo due punti qualsiasi di coordinate P₁(x₁,y₁) e P₂(x₂,y₂). Non spaventa nessuno calcolare la distanza tra questi due punti. Ci viene in soccorso il teorema di Pitagora, che ci dice:

d² = (x₂ - x₁)² + (y₂ - y₁)²

Se, adesso cambiassimo (Fig. 10) il sistema di riferimento (ad esempio x’,y’) i due punti cambierebbero entrambi di coordinate e diventerebbero P₁(x’₁,y’₁) e P₂ (x’₂,y’₂).

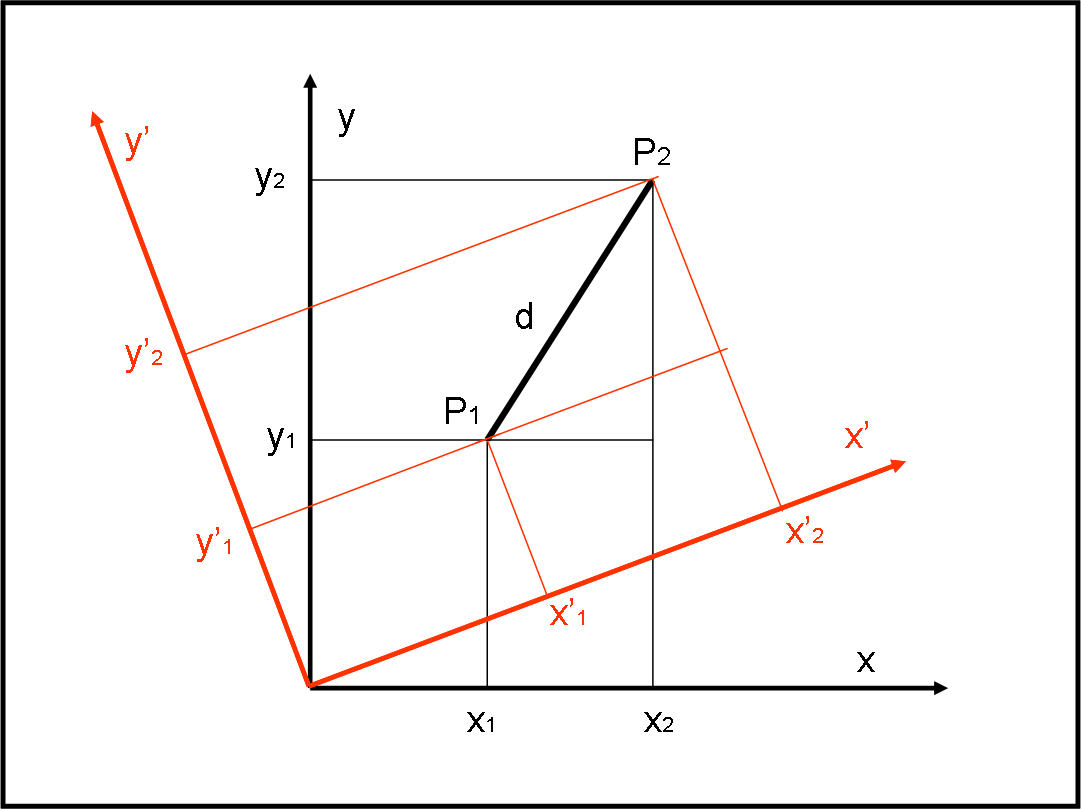
La loro distanza potrebbe essere nuovamente calcolata con il teorema di Pitagora nel nuovo sistema di riferimento, ma troveremmo, senza ombra di dubbio, che:

d’² = (x’₂ - x’₁)² + (y’₂ - y’₁)² = (x₂ - x₁)² + (y₂ - y₁)² = d²

Potremmo provare a calcolare la distanza eseguendo tutte le trasformazioni di assi cartesiani, ma troveremmo sempre che la distanza rimane immutata. Possiamo concludere che essa è invariante rispetto al sistema di riferimento. Questo è ciò che capita in uno spazio euclideo (chi avesse voglia, tanto per richiamare un po’ di matematica e geometria, potrebbe dimostrare la relazione precedente…).

Divertiamoci ancora un po’ con questo invariante. Abbiamo ribadito che la distanza non dipende dal sistema di riferimento, per cui possiamo considerare in un certo sistema un punto O e una distanza R. Da quanto sappiamo, nel piano euclideo, possiamo disegnare senza problemi, in Fig. 11, il luogo dei punti che hanno la stessa distanza R dal punto O.

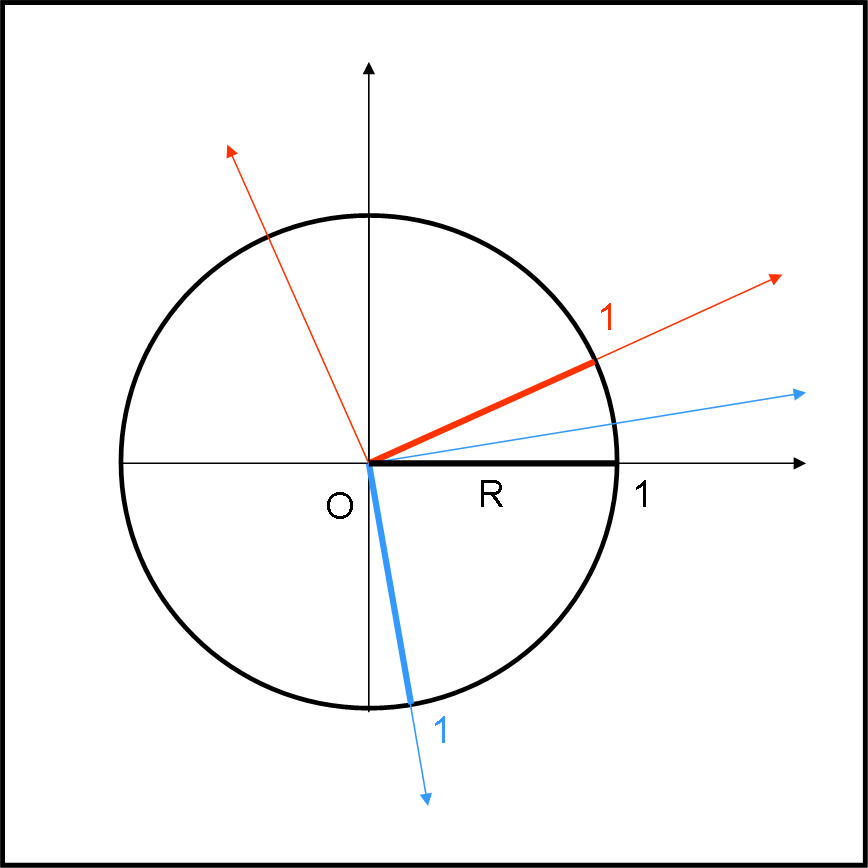
Ciò che viene fuori lo conosciamo molto bene! Non è altro che una circonferenza di centro O e di raggio R. Il piano euclideo permette tante bellissime rappresentazioni. Questa è la più semplice, ma ne esistono molte altre che ben conosciamo, come le coniche in genere e tante altre curve.

Studiamo ancora meglio la nostra circonferenza costruita come luogo di punti. Immaginiamo che il raggio sia una distanza unitaria, ossia sia l’unità di misura. Ne segue che qualsiasi rotazione del sistema di riferimento ammette sempre la stessa unità di misura.

Un discorso analogo lo abbiamo appena fatto per il diagramma di Minkowski. In modo un po’ empirico, ci siamo costruiti il luogo dei punti che mantiene la stessa unità di misura, attuando la trasformazione di Lorentz per diversi valori della velocità v. Abbiamo trovato una circonferenza? Nemmeno per sogno. Abbiamo costruito una doppia iperbole equilatera con asintoti nelle rette con v = c. C’è qualcosa che non va… o -quantomeno- siamo costretti a dire che il piano spaziotempo di Minkowski non può essere euclideo, altrimenti avremmo dovuto trovare una circonferenza. Da qui non si scappa.

In altre parole, siamo stati capaci di trovare una “distanza” che rimane sempre uguale a se stessa (uguale a “1”, per esempio), ma che descrive una curva ben diversa dalla circonferenza. Una distanza che nel nostro modo di vedere “classico” ci appare descrivere distanze variabili da caso a caso, ma che nello spaziotempo di Minkowski sono costanti.

Una distanza che non può avere niente a che fare con la distanza dello spazio euclideo. Non ci vuole molto a dimostrarlo, considerando le equazione che descrivono la trasformazione di Lorentz. Se calcoliamo la distanza “euclidea” (attraverso il teorema di Pitagora) nel sistema S(T,x) e nel sistema S’(T’,x’) troveremmo due grandezze completamente diverse.

In parole matematiche:

T² + x² ≠ T’² + x’²

Un risultato questo che conosciamo già benissimo dato che abbiamo dimostrato che un asta rigida cambia la propria lunghezza a seconda del riferimento usato (contrazione di Lorentz).

Possiamo, perciò, ribadire un paio di concetti già definiti molte volte: la trasformazione di Lorentz trasforma un sistema ortogonale in un sistema non ortogonale e l’unità di misura è variabile da sistema a sistema. Tuttavia, questa unità di misura rimane costante nello spazio non euclideo di Minkowski. Ciò che nel piano ortogonale “classico” ci sembra variabile, nel piano trasformato non euclideo di Minkowski  è costante. Proprio questo tipo di trasformazione causa le ben note dilatazione dei tempi e contrazione delle lunghezze. D’altra parte, abbiamo visto che questa trasformazione si può ricavare considerando soltanto la relatività della simultaneità. Tutto torna sempre al punto di partenza. Se rileggete i capitoli precedenti, trovate, infatti, che siamo riusciti a costruire gli assi trasformati e le loro unità di misura, utilizzando solo il concetto di simultaneità relativa.

Abbiamo dedotto che la distanza euclidea NON si mantiene nel diagramma di Minkowski. In altre parole, la distanza calcolata con il teorema di Pitagora, non è un’invariante nello spaziotempo. Tuttavia, siamo riusciti a trovare una curva che descrive il luogo dei punti che mantengono una distanza spaziotemporale costante. Essa è l’iperbole che abbiamo ricavato precedentemente.

Ricordiamo ciò che avevamo già trovato nel capitolo “Appendice preveggente” della RR, dopo aver fatto conoscenza con l’orologio a luce:

c² Δt’² = c²Δt² - Δx²

ossia:

ΔT’² = ΔT² – Δx²

O, partendo dall’origine:

T’² = T² – x²

Il primo membro non è altro che il tempo proprio misurato nel sistema S’. Ma il tempo proprio deve sempre essere lo stesso in qualsiasi sistema di riferimento.

In realtà, T’ è un “intervallo”, dato che si è ottenuto moltiplicando il tempo per la velocità della luce ed è, quindi, diventato una distanza a tutti gli effetti. Sarebbe più corretto dire che esso rappresenta la distanza percorsa dalla luce in un intervallo di tempo proprio. Dimostriamo, comunque, che questo “intervallo” è invariante.

Si può dimostrare con pochi passaggi…

T’² – x’² = (T – βx)²/(1 – β²) – (x – βT)²/ (1 – β²) = (T² + β²x² - 2βTx – x²  - β²T² + 2βTx)/ (1 – β²) = (T² + β²x²– x²  - β²T²)/(1 – β²) = (T² (1 - β²) – x² (1- β²))/(1 – β²) = T² – x²

Il tempo proprio (l’intervallo di prima) è, quindi, una costante per qualsiasi sistema di riferimento. Se consideriamo come valore costante proprio l’unità di misura, otteniamo la relazione.

T² – x² = 1

Essa descrive la curva luogo dei punti in cui il tempo proprio è uguale all’unità. Esattamente l’equivalente, nel piano x,T della circonferenza nel piano x,y. Tale curva, nel piano x,T  rappresenta, quindi, il luogo dei punti con distanza temporale unitaria per qualsiasi sistema in movimento. Proprio ciò che avevamo trovato per via empirica.

L’equazione precedente è quella di un’iperbole equilatera che ha asintoti nelle rette y = x e y = -x.  Se volete saperne di più, basta che andiate a vedere nel capitolo relativo all’iperbole come “conica” nelle lezioni di matematica.

Inoltre, essa taglia l’asse T proprio nel punto T = 1. Basta, infatti, porre x = 0 e si determina che T = 1. Questa curva ci regala l’unità di misura in tutti i sistemi S’ di coordinate T’ e x’. Infatti, abbiamo appena dimostrato che:

T² – x² = T’² – x’² = 1

E, quindi, per x’ = 0, avremo anche che T’ = 1.

In parole molto povere, l’intersezione dell’iperbole sopra descritta con qualsiasi asse T’ (relativo a un sistema S’ in movimento rispetto a S), che ha come equazione T = x/β, indica l’evento che ha la stessa unità temporale rispetto a O. In pratica: l’iperbole con la costante uguale a 1 ci dice dove risiedono i punti che distano la stessa “distanza” uguale a 1 rispetto a O. Scegliendo una velocità v di spostamento di S’ otteniamo un asse T’. Il punto (o meglio l’evento) dove esso interseca l’iperbole ci regala l’unità di misura sull’asse T’.

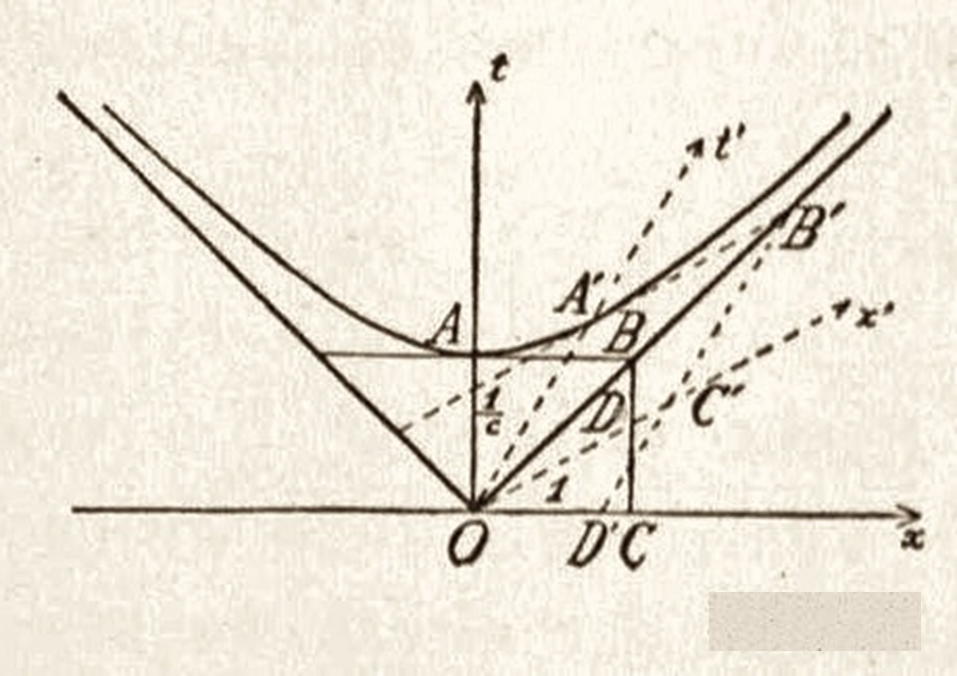
Non è quindi difficile comprendere perché le iperboli ottenute per vari valori della costante (1,2, 3,…) sono dette curve di calibrazione. E’ estremamente interessante riassumere quanto detto finora, utilizzando proprio la figura disegnata da Minkowski, riportata nella Fig. 12. Potete anche notare come l’asse trasformato x’ (quello di simultaneità) risulta tangente alla curva di calibrazione nel punto intersezione prima costruito. Nella figura leggete t e t’ e non T e T’. Ma le cose non cambiano, dato che si vede un 1/c che nel caso di T = ct, diventa proprio 1/1 = 1.

Cerchiamo, adesso, di fare attenzione e di non confonderci… I sistemi di riferimento che viaggiano con velocità v rispetto a quello “fermo” subiscono una trasformazione che rende i loro assi non ortogonali e tali che l’invariante non è più la distanza pitagorica ma qualcosa di diverso, ossia il tempo proprio o, meglio, la distanza percorsa dalla luce nell’intervallo di tempo proprio. Esso è anche l’unità di misura dell’asse T’ di questi sistemi in moto e rimane, quindi, sempre uguale  a 1. Tuttavia, variando v, essa appare diversa se paragonata a quella del sistema fermo S. Ne segue che è estremamente interessante calcolare il fattore di variazione dell’unità di misura rispetto a quella del sistema fermo, che è ortogonale per definizione (non ha subito nessuna trasformazione). Su di lui vale ancora il teorema di Pitagora…

Passiamo al calcolo e i dubbi spariscono velocemente.

Consideriamo la Fig. 13, che è poi quella di Minkowski. Ciò che vogliamo calcolare è il rapporto, misurato nel sistema fermo S, tra la lunghezza dell’unita di misura del sistema S’ e quella del sistema fermo S. L’unità di misura di T’ non è altro che l’intersezione tra la retta T’ (ossia T = x/β) e le curva di calibrazione con la costante uguale a 1, ossia T² – x² = 1. Come vedete disegniamo tutto sul piano x,T.

L'evento A’, intersezione tra T’ e la curva di calibrazione, è dato dal sistema

T² – x² = 1

T = x/β

Un sistema veramente banale che ci permette di ricavare velocemente il valore di T, ossia la coordinata di A’ nel sistema S.

Sostituendo la seconda equazione nella prima si ha:

x²/β² – x² = 1

(x² - β²x²)/β² = 1

x²(1 - β²) = β²

x² = β²/(1 - β²)

x = β/(1 - β²)^1/2

Sostituendo questo valore nella seconda equazione del sistema, abbiamo subito:

T = x/β = β/(β (1 - β²)^1/2)

T = 1/(1 - β²)^1/2

Queste sono le coordinate di A’ nel sistema ortogonale S.

Possiamo, quindi, calcolare la “distanza” A’O utilizzando il teorema di Pitagora (nel sistema (x,T) posso usarlo!):

OA’² = x² + T² = β²/(1 - β²) + 1/(1 - β²)

OA’ = ((1 + β²)/(1 - β²))^1/2 > OA = 1

L’unità di misura di ogni sistema di riferimento in moto è maggiore dell’unità di misura del sistema “fermo” e subisce una dilatazione che cresce con la velocità v. Possiamo dunque affermare che la trasformazione di Lorentz corrisponde a una rotazione degli assi e a una dilatazione della unità di misura. E’ proprio questa dilatazione delle unità di misura la responsabile della contrazione delle lunghezze e della dilatazione del tempo. Quest’ultima si vede già benissimo nella figura… ma non corriamo troppo. Ogni cosa a tempo debito.

La costanza del tempo proprio rispetto al cambiamento degli assi, ci porta, però, alla definizione di qualcosa di ancora più generale. La grandezza

T² – x²

Essa è invariante per tutto lo spazio di Minkowski e il suo significato può essere quello di una vera e propria “distanza” spaziotemporale. Possiamo scriverla:

s² = T² – x²

Essa può assumere valori maggiori e minori di zero (non spaventatevi!). Il primo caso che ci porta alla definizione del luogo dei punti aventi lo stesso tempo proprio. Tuttavia, ponendo:

s² = T² – x² < 0

si entra nella zona che sta sotto alla retta descritta dalla luce (v = c). Ponendo:

T² – x² = - 1

Si costruisce l’altra iperbole, quella che determina l’unità di misura sull’asse delle x’.

Fermiamoci un attimo… Questa parte del diagramma di Minkowski ha un significato completamente differente da quella descritta dall’iperbole precedente.

Basta riflettere sull’ultima formula scritta. Essa è in realtà il quadrato di un qualcosa (s). Malgrado ciò è stata posta uguale a meno 1. E ciò sembrerebbe impossibile! Come fa un quadrato a essere negativo? Siamo entrati nel mondo dei numeri immaginari, ma non reputo importante affrontarli, almeno in questo caso. Possiamo capire benissimo quali sono le conseguenze, studiando cosa capita nelle varie zone del diagramma di Minkowski. In tal modo, esso diventerà qualcosa di ben più generale e descrittivo di una semplice trasformazione di coordinate. Bisognerà, perciò, capire molto bene cosa s’intende per eventi, che tipi di eventi avvengono e come e se possono essere connessi tra loro. Un discorso da fare con molta calma…

Per chi vuole cominciare a rifletterci sopra (ma non ponendo domande… dato che ci torneremo con la dovuta calma)  aggiungo questa frase molto esplicativa: “l’intervallo spaziotemporale (l'invariante) risulta positivo o negativo a seconda che due eventi risultino più o meno vicini nello spazio quando vengono confrontati con lo spazio percorso da un segnale luminoso”. Da ciò deriva il fatto che non tutti gli eventi possono realmente essere connessi tra loro… la velocità della luce è una … severa maestra!

Ci torneremo, ci torneremo… abbiate pazienza. Tuttavia, abbiamo già in mano tutti i parametri per affrontare la dilatazione dei tempi (immediata), la contrazione delle lunghezze (meno immediata) e il paradosso dei gemelli in modo essenzialmente grafico e molto più completo di quanto fatto finora.

Divertiamoci un po’…