La serie di articoli dedicati ai cerchi di Archimede è inserita nella pagina d'archivio Antichi Greci, che passione!

 

Continuiamo a divertirci con il nostro "arbelos" e a scoprire alcune delle sue innumerevoli proprietà. Dato che non vi sono stati  tentativi di dimostrazione, mettiamola pure in chiara evidenza.

Dalla definizione di arbelos nascono due semplici conseguenze, che sono l'inizio di una serie lunghissima di altre escogitate durante i secoli. Limitiamoci, per adesso, alle due più semplici:

1)  Il perimetro di un arbelos è uguale alla circonferenza in cui sono inscritti i due cerchi.

La soluzione è praticamente immediata... Il perimetro dell'arbelos (vedi Fig. 1 dell'articolo 1a) è dato dalla somma della semicirconferenza di diametro  AB più le due semicirconferenze di diametro AN e NB. La qualcosa può essere scritta come:

P arb = (1/2)( 2 π AB/2) + (1/2)( 2π AN/2) + (1/2)( 2 π BN/2) = π AB/2 + π AN/2 + π NB/2

P arb = π /2(AB +AN+ NB) =  π/2(AB + AB) = π AB

Ma la circonferenza di diametro AB vale proprio:

C_AB = 2 π AB/2 = π AB

2) Costruiamo l'arbelos e indichiamo con P il punto di intersezione, con la circonferenza di base, della retta perpendicolare ad AB passante per N. Uniamo P con A e P con B. Queste rette intersecano le due circonferenze in H e K. Il quadrilatero PHNK è un rettangolo.

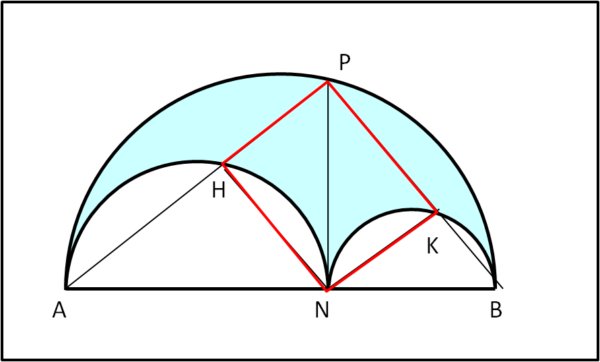
La soluzione è veramente ovvia, ricordando che APB, AHN e NKB sono angoli retti. Lo sono, quindi, anche NKP e NHP. Il quadrilatero ha quindi tre angoli retti e tale deve essere anche il quarto (360 - 90 - 90 - 90 = 90).

Passiamo adesso al lemma 6, di soluzione decisamente più complicata. La sua applicazione sembrerebbe poco utile, ma chiedetelo a Pappo e alla sua celebre catena...

Lemma 6

Costruiamo il nostro arbelos, facendo in modo che il diametro del cerchio inscritto maggiore sia uguale a 3/2 di quello minore, ossia AC = 3/2 BC (qualsiasi rapporto andrebbe comunque bene). Costruiamo un cerchio che sia tangente ai due cerchi inscritti e a quello di base di diametro AB. Se GH è il diametro di questo cerchio, determinare il rapporto tra GH e AB.

Questa volta si tratta proprio di un "quiz". La sua soluzione, con il metodo classico, ha bisogno di grande accortezza e -lasciatemelo dire- fantasia unita a logica ferrea. Resta, comunque, il fatto che i passaggi sono estremamente elementari. Volete provare?

In Fig. 10 inseriamo i dati e indichiamo i punti di tangenza con le lettere D, E, F.

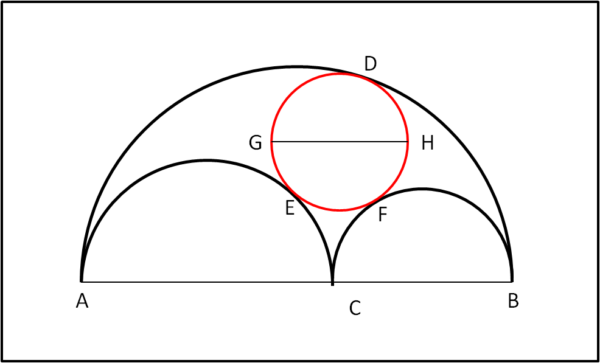
Tracciamo i segmenti AG, GD,BH e HD. Per il lemma 1, AGD è una retta così come lo è DHB. Analogamente, lo sono GFB, HEA, CEG e CFH. Tracciamoli nella Fig. 11

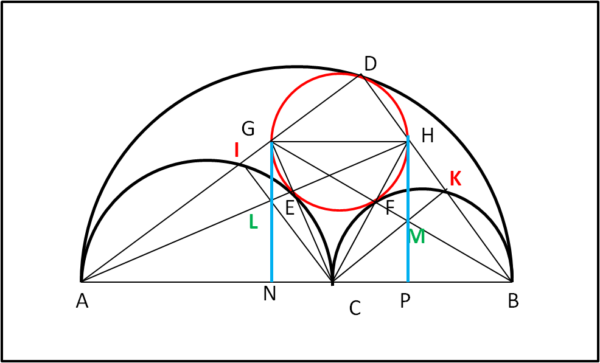
Si individuano i punti I,K, E ed L. Tracciare GL e HM. Questi due ultimi segmenti possono essere prolungati fino a incontrare AB in N e P (Fig. 12)

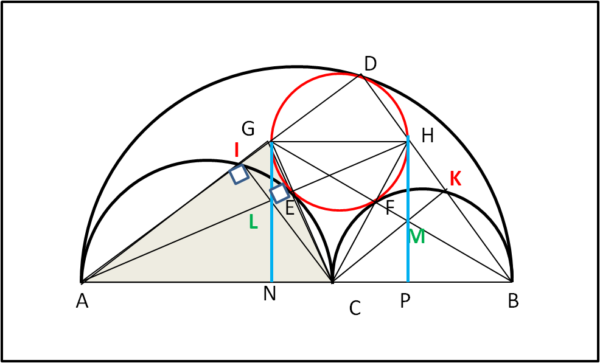
Nel triangolo AGC l’angolo in I e l’angolo in E sono retti. Ne segue che AI e AE sono altezze e si incontrano in L. Il segmento GN passa per L per costruzione. Ne segue che GN è la terza altezza, ossia l’angolo in  N è retto. Stesso discorso vale per  il triangolo CHB e per il segmento HMP. Si può, quindi, concludere, ricordando che GH//AB, per costruzione, che

GH = NP.

Consideriamo il triangolo AHB di Fig. 13

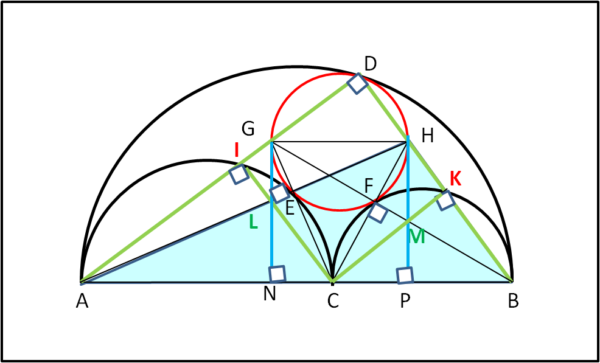
Gli angoli in I e in D sono retti, per cui LC è parallela ad HB. Vale perciò la proporzione:

AC/CB = AL/LH

Dai triangoli rettangoli ALN e AHP, sappiamo, però, che:

AL/LH = AN/NP

e quindi:

AC/BC = AN/NP            .... (6)

Analogo discorso vale per il triangolo AGB di Fig. 14

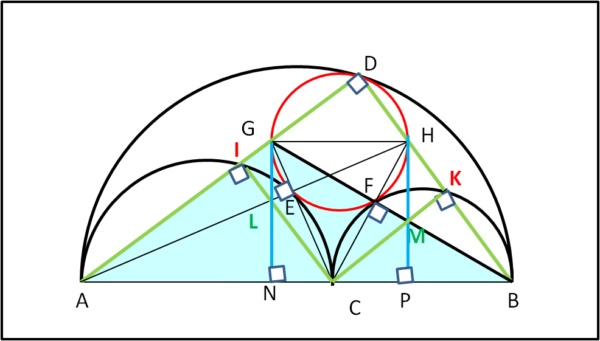
Si ha:

AC/CB = GF/FB

Ma dai triangoli rettangoli GNB e MPB si ricava:

GF/FB = NP/PB

In conclusione:

AC/AB = NP/PB               .... (7)

Dalla (6) e dalla (7) si ha:

AN/NP = NP/PB              .... (8)

Inseriamo il dato di partenza, ossia AC/BC = 3/2. Per la (7) e la (8) vale perciò anche che, :

AN/NP = 3/2

ossia:

AN = 3/2NP

Per la (8) si ha:

AN PB = NP²

3/2 NP PB = NP²

PB = 2NP²/3NP = 2/3 NP

Scriviamo, allora, AB in funzione del solo NP = GH

AB = AN + NP + PB

AB = 3/2 NP + NP + 2/3 NP

AB = NP(3/2 + 1 + 2/3) = NP (9 + 6 + 4)/6 = 19/6 NP

NP = 6/19 AB                  .... (9)

che è la risposta al "quiz" di Archimede.

Sembrerebbe un risultato di relativa importanza, ma è stato la base per la celebre catena di Pappo di Alessandria (vedi Fig. 15), che ancora oggi fa discutere  e solleva nuove interpretazioni e dimostrazioni. Il punto fondamentale è che la proporzione è "continua" (i medi sono uguali tra loro). Per qualsiasi valore di k si ha:

GH/AB = k/(1 + k + k²)

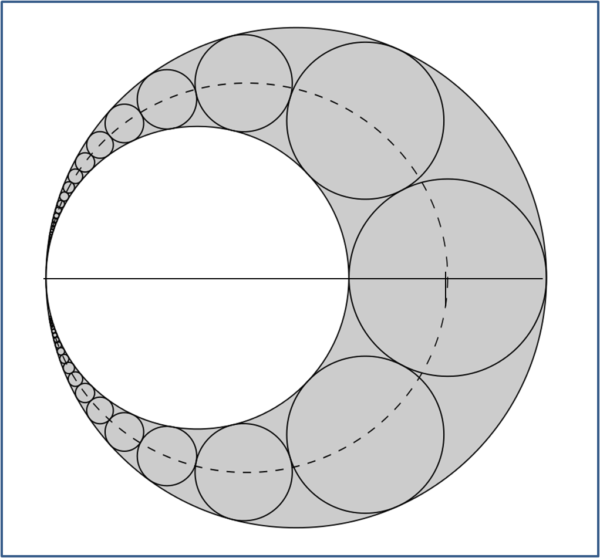
Non è il caso, per il momento almeno, di studiarla più a fondo. Basti dire che il luogo dei centri delle varie circonferenze inscrivibili nell'arbelos è un'ellisse di semiasse maggiore uguale alla media aritmetica del cerchio di partenza (R) e di quello della circonferenza fissa (r)  La dimostrazione è banale, come illustra la Fig. 16

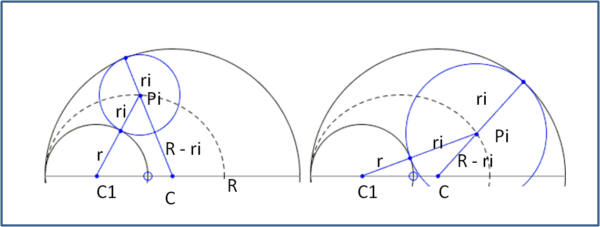
La distanza CPi + PiC1 può essere scritta, per qualsiasi valore del centro Pi, come:

CPi + PiC1 = R – ri + r + ri = R + r

La distanza è una costante e quindi il luogo dei Pì è un’ellisse che ha fuochi C1 e C. Il suo semiasse è, ovviamente, (R + r)/2.

continua...