Categorie: Matematica
Tags: area geometria quiz triangolo qualsiasi
Scritto da: Vincenzo Zappalà
Commenti:9
Calcolare l'area di un triangolo? Basta allacciarsi le scarpe! **
Un semplice quiz che ci introdurrà a un problema veramente interessante.
Inizio questo argomento proponendo un quiz decisamente semplice, ma che sarà utile per quando le cose cominceranno a complicarsi un pochino e l'argomento diventerà molto più generale.
La figura che segue mostra un triangolo, di cui conosciamo le coordinate dei tre vertici.
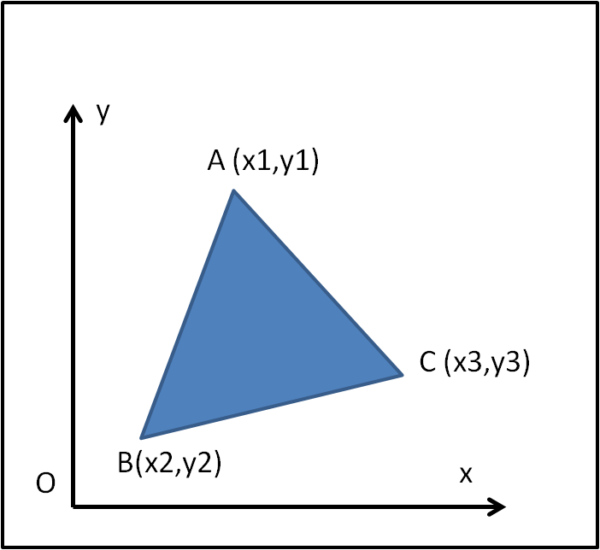
Si chiede di calcolare l'area del triangolo, facendo uso delle sole quattro operazioni: somma, sottrazione, moltiplicazione e divisione. In altre parole, niente trigonometria e nemmeno teoremi di Pitagora.
Sarebbe cosa ben fatta se la formula finale fosse scritta in modo "ordinato", in modo da poterne trarre una visione più generale.
Ah, dimenticavo il titolo... per adesso non fateci caso!
QUI il proseguimento (con la soluzione)






9 commenti
Per prima cosa effettuiamo un cambio di coordinate togliendo il valore di uno dei vertici, pe (x3,y3) sottraendo x3 da x1 e x2 e y3 da y1 e y2.
Chiamiamo A il nuovo punto x1y1 e B il punto x2y2. L origine sarà O.
Prolunghiamo il lato AB fino a incontrare l asse x nel punto incognito x4. Chiamiamo C questo punto che avrà coordinate (x4,0).
X4 si trova utilizzando la formula di retta per 2 punti:
(x4 - x1)/(x2-x1 )= -y1/( y2-y1 )
Siamo adesso in presenza di tre triangoli: OAB , OAC e OBC.
L area di OAC è uguale a y1 x4 /2.
L area di OBC è y2 x4/2 .
L area cercata è OAB = OAC – OBC.
Caro Leandro,
che ne dici di cercare di generalizzare la formula? Avviciniamoci alle scarpe...
Caro Enzo, dunque per risolvere il problema io pensavo di costruire un rettangolo intorno al triangolo i cui vertici cadessero su alcuni punti del perimetro del rettangolo.
Gli angolo di tale rettangolo hanno le seguenti coordinate: (X2;Y2) che coincide con il vertice in basso a sinistra del triangolo; (X3;Y2); (X3;Y1); (X2;Y1).
In questo modo tra il perimetro del triangolo e quello del rettangolo ottengo tre triangoli rettangoli che coprono gli spazi che separano i due perimetri (purtroppo non posso fare una figura, per cui bisognerà accontentarsi della descrizione).
A questo punto, ricordando che l’area di un rettangolo è uguale a base x altezza e quello di un triangolo rettangolo a (cateto x cateto)/2, è sufficiente sottrarre all’area del rettangolo quella dei tre triangoli rettangoli per ottenere l’area del triangolo richiesta dal quiz.
Area = (X3 – X2) (Y1 – Y2) – (X3 – X2) (Y3 – Y2)/2 – (X3 – X1) (Y1 – Y3)/2 – (X1 – X2) (Y1 – Y2)/2
Area = (X3Y1 – X3 Y2 – X2 Y1 + X2Y2) – (X3Y3 – X3Y2 – X2Y3 + X2Y2)/2 – (X3Y1 – X3Y3 – X1Y1 + X1Y3)/2 – (X1Y1 – X1Y2 – X2Y1 + X2Y2)/2
Area = (2X3Y1 – 2X3 Y2 – 2X2 Y1 +2X2Y2 – X3Y3 + X3Y2 + X2Y3 – X2Y2 – X3Y1 + X3Y3 + X1Y1 – X1Y3 – X1Y1 + X1Y2 + X2Y1 – X2Y2)/2
Area = (
2X3Y1 –2X3 Y2 –2X2 Y1 +2X2Y2–X3Y3+X3Y2+ X2Y3 –X2Y2–X3Y1+X3Y3+X1Y1– X1Y3 –X1Y1+ X1Y2 +X2Y1–X2Y2)/2Area = (X3Y1 – X3 Y2 – X2 Y1 + X2Y3– X1Y3 + X1Y2)/2
Area Triangolo = (X3 (Y1 –Y2) – X2 (Y1 –Y3) – X1 (Y3 – Y2))/2
A giudicare dal risultato applicabile a qualunque triangolo di cui si conoscono le coordinate cartesiane dei vertici, per calcolare l’area basta moltiplicare la coordinata X del vertice più a destra sull’asse delle ascisse X (nel nostro caso X3) per la differenza delle coordinate Y degli altri due vertici (nel nostro caso Y1 –Y2 ) a cui occorre sottrarre le altre due coordinate X (dei vertici del triangolo, nel nostro caso X2 e X1), moltiplicate per la differenza delle coordinate Y degli altri due vertici rispetto a quello preso in considerazione, il tutto diviso per 2.
Paolo
Dimenticavo, volendo si può fare lo stesso usando le coordinate Y, ossia si passa da:
Area = (X3Y1 – X3 Y2 – X2 Y1 + X2Y3– X1Y3 + X1Y2)/2
Area = (Y1 (X3 –X2) – Y2 (X3 – X1) –Y3 (X1 – X2))/2
Paolo
Già meglio, ma si può generalizzare ancora di più e... pensare anche a poligoni con un numero n di lati... Ricordatevi di allacciare le scarpe...
Così a occhio mi sembra che vada moltiplicata la coordinata X di un angolo per la differenza delle coordinate Y del lato opposto, oppure quelle Y dell'angolo per la differenza di quel X del lato opposto.... sempre tutto diviso 2... ma dovrei fare delle prove con dei poligoni.
Paolo
domani vado via per 6 giorni (viaggio culturale a Ravenna, Ferrara e Mantova...). Avete tutto il tempo per pensarci, provare e avere l'idea risolvente...
L'area del triangolo si ottiene dall'area del trapezio rettangolo avente basi y1 e y3
ed altezza x3 - x1 sottraendo le due aree dei trapezi:
di basi y1 , y2 ed altezza x2-x1 e
basi y2,y3 ed altezza x3-x2
L'area del trapezio si calcola sommando le due basi (ordinate) e moltiplicandole per l'altezza (differenza delle ascisse) , diviso 2.
La sua area sarà quindi la metà di
(y1+y3) (x3-x1) +
(y1+y2) (x1-x2) +
(y2+y3) (x2-x3)
Svolgendo i calcoli si ottiene
y1 x3 -y3 x1 +
y2 x1 - y1 x2 +
y3 x2 - y2 x3
La regola generale è somma dei prodotti della ordinata di un vertice moltiplicato per l' ascissa del vertice successivo meno la somma dell'ordinata di un vertice per l'ascissa del vertice precedente (ordinati ciclicamente).
La regola si estende a qualunque poligono convesso di n lati.
E le stringhe delle scarpe ?
Beh, se ordiniamo i valori delle ascisse e delle ordinate in due colonne affiancate ed uniamo i punti che formano i prodotti si riproduce lo schema di una scarpa allacciata :
quasi perfetto Landro!