Categorie: Matematica
Tags: geometria elementare numero delle facce piramide solidi tetraedro volume
Scritto da: Vincenzo Zappalà
Commenti:13
Gli esami non finiscono mai... **
Non è raro che alcune soluzioni di problemi presentati nei "test" per l'ammissione a scuole superiori risultino sbagliate. Chi li prepara dovrebbe, probabilmente, essere veramente all'altezza della situazione. Questi "infortuni" non sono però tipici dell'Italia, dato che un caso plateale è capitato anche negli Stati Uniti e si è anche cercato di arrampicarsi sui vetri.
Il problema è molto semplice e la risposta sembrerebbe altrettanto semplice... ma è proprio così?
Consideriamo due solidi geometrici ben conosciuti: un tetraedro con tutti gli spigoli uguali all'unità e una piramide a basa quadrata, avente anch'essa tutti gli spigoli uguali all'unità.
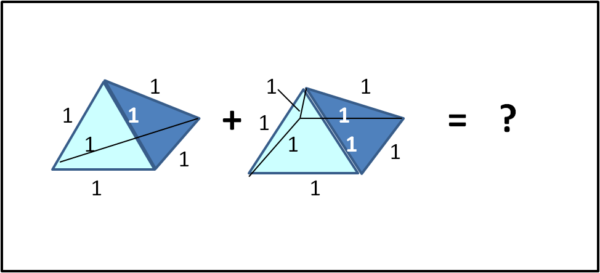
Se facciamo coincidere una faccia triangolare del tetraedro con una faccia triangolare della piramide, otteniamo un nuovo solido.
Nel test veniva chiesto: Quante facce ha il nuovo solido?
Beh... la risposta attesa dalla commissione d'esame era sbagliata. Un sedicenne diede la risposta giusta, ma la commissione decise , sperando forse di non perdere la "sua" faccia, di accettare comunque anche la risposta sbagliata. E' proprio vero che gli esami non dovrebbero finire mai...
Vi invito a dare l'unica risposta giusta e a dimostrarla. Non sarebbe male, dopo, costruirsi i due solidi con del cartoncino e vedere ciò che viene fuori.
Per non farci mancare niente, aggiungo qualche domanda del tutto personale (sperando di non sbagliare la risposta...):
Se considerassimo due piramidi a base quadrata con gli spigoli tutti uguali e facessimo combaciare una faccia triangolare, quante facce avrebbe il nuovo solido?
E se facessimo lo stesso con due tetraedri con tutti gli spigoli uguali?
E se considerassimo le due piramidi e facessimo combaciare le basi quadrate?
Infine:
Qual è il rapporto tra il volume del tetraedro e quello della priamide a base quadrata?
N.B.: La soluzione dovete darla senza l'uso di geogebra o cose simili.
Buon divertimento...
Qui una soluzione
13 commenti
il numero delle facce del nuovo solido corrisponde alla somma dei lati dei poligoni base delle piramidi.
le facce delle piramidi sono x+1 dove x è il numero dei lati del poligono base. Le facce coincidenti non fanno parte del nuovo solido e vanno tolte, una per solido. Per cui (x+1 -1) + ( y+1-1)
il volume del tetraedro è la metà del volume della piramide a base quadrata.
Il volume non è la metà... le altezze dei 2 solidi non sono uguali.
Ho cercato di visualizzare il solido “somma” piramide a base quadrata e tetraedro (mi sono aiutato con gli….stuzzicadenti per “”vederli” entrambi);
Una faccia triangolare della piramide ed una triangolare del tetraedro si dispongono sullo stesso piano a “destra” (1 faccia somma), stessa cosa a “sinistra”(1 faccia somma), rimane una faccia triangolare di “dietro” della piramide (1 faccia), la faccia quadrata della piramide (1 faccia ) e una faccia triangolare del tetraedro (1 faccia):
in totale 5 facce.
Con le stesse “visioni” tetraedro + tetraedro = solido a 4 facce
piramide + piramide unite per una faccia triangolare = solido a 6 facce
piramide + piramide unite per la base quadrata = solido a 8 facce
Per i volumi conviene sezionare la piramide partendo dal vertice, o secondo una diagonale della base quadrata o secondo la mediana di un lato per visualizzare triangoli rettangoli e calcolare l'altezza della piramide (che è il cateto di un triangolo rettangolo ma visto sul piano).
P.S.
S è tutto o parzialmente sbagliato, non chiamatemi "visionario"
Mi sa che tetraedro + tetraedro mostrano 6 facce
I ragazzini dell'esame non potevano costruire qualcosa con gli stuzzicadenti... ne segue che si può dimostrare anche solo con la grafica...
caro Andy, se un tetraedro e una piramide danno due coppie di facce complanari, possono anche farlo due piramidi?
Per il volume mettetevi d'accordo...
Caro Enzo,
le mie "visioni" erano in parte distorte.
Innanzitutto posto le immagini di due modellini costruiti molto ma molto "artigianalmente":
questo è il solido tetraedro + piramide, con le facce 1 e 2 complanari, la faccia 5 dietro, la 4 alla base, la 3 sotto la "prua",
mentre questa è l'immagine del solido piramide + piramide, unite secondo la faccia triangolare:
a meno che non abbia sbagliato nella costruzione del modellino, qui non vedo facce complanari, il solido risultante presenta 8 facce.
Ho dispiegato sul piano la piramide ed il tetraedro:
successivamente ho disegnato l'immagine tetraedro + piramide con le due facce triangolari sovrapposte proiettate ortogonalmente sul piano (la line rossa):
mentre questa è l'immagine delle piramidi "incollate" secondo una faccia triangolare:
Nel caso tetraedro + piramide, le basi dei triangoli che diverranno complanari una volta richiusi nello spazio tridimensionale, racchiudono un angolo di 150°,
nel caso piramide + piramide unite da una faccia triangolare, le basi dei triangoli si trovano sulla stessa retta, e una volta richiusi non sembrano complanari.
Per quanto riguarda la misura dei volumi, il volume del tetraedro è pari a:
(√2 / 12) × L^3 (dove L è la misura dello spigolo)
quello della piramide è pari a (1 / 3) × L^2 × h (h è la misura dell’altezza calcolata dal vertice opposto alla base quadrata).
Dato che la proiezione del vertice opposto alla base quadrata ricade sul baricentro della base stessa,
l’altezza sarà la misura del cateto di un triangolo rettangolo che ha per ipotenusa lo spigolo e come altro cateto metà diagonale del quadrato di base;
oppure (ma la misura sarà uguale al caso precedente) il cateto di un triangolo rettangolo avente per ipotenusa l’altezza di una faccia triangolo equilatero e come altro cateto metà base:
nella prima ipotesi h = √( 1^2 - (√2 / 2)^2) ) = √( 1 – 1/2) = √2 / 2
nella seconda ipotesi h = √( (√3 / 2)^2 – (1 / 2)^2) ) = √(3 /4 – 1/4) = √2 / 2
Volume tetraedro = (√2 / 12) × 1^3 = √2 / 12
Volume piramide = (1 / 3) × 1^2 × √2 / 2 = √2 / 6
il rapporto volume tetraedro / volume piramide a base quadrata sarà:
(√2 / 12) / (√2 / 6) = 1 / 2
caro Andy,
evviva i modellini! Tuttavia, si può anche dimostrare la complanarità ragionando su una semplice figura... Cosa che ha fatto sicuramente il ragazzino che ha stravolto i professori!
Il solido che si forma ha 5 facce poiché, oltre alle 2 che scompaiono nella unione, altre due si uniscono essendo complanari (5+4-2-2=5).
Credo che la chiave di una possibile dimostrazione della complanarità delle due facce sia stabilire che l'altezza della piramide e la distanza tra lati opposti del tetraedro sono uguali (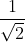
). Sono entrambe i cateti di un triangolo rettangolo che ha come ipotenusa l'altezza del triangolo equilatero (
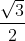) della faccia in comune e come altro cateto la meta di un lato (
).
Da qui si può dimostrare che i lati opposti della facce laterali che si forma dalla unione dei due solidi sono paralleli e quindi sono sullo stesso piano.
Provo a fare una figura leggibile che illustri gli elementi utilizzati sopra.
Graficamente su spazio bidimensionale:
Tridimensionalmente, la figura 5 rappresenta un prisma trapezoidale isoscele, con una base rettangolare che presenta uno spigolo maggiore doppio dello spigolo minore, che a sua volta è uguale a tutti gli altri spigoli presenti (esclusi ovviamente i due lati-spigoli “lunghi” della base rettangolare).
Operando sul prisma un taglio partendo dal vertice alto di sinistra con un piano parallelo alla faccia triangolare di destra, diretto verso la base e, parimenti,
operando un taglio partendo dal vertice alto di destra con un piano parallelo alla faccia triangolare di sinistra, diretto verso la base,
ed estraendo il pezzo ottenuto, questo pezzo è il tetraedro regolare.
Questa è la figura
Cari amici, sto pensando anch'io a una dimostrazione ben visibile delle proiezioni dei vari solidi sui piani xy, xz e yz. Andy ha azzeccato in pieno la dimostrazione tridimensionale relativa a tetraedro e piramide. Relativamente a Fabry, vorrei chiedere cosa intende per "distanza tra i lati opposti del tetraedro..."
Esplicito il ragionamento che penso possa essere la traccia di una dimostrazione che nella composizione dei due solidi ci sono due lati della piramide complanari a due lati del tetraedro.
Se taglio il solido composto con il piano di simmetria che passa per il segmento VT, ottengo due triangoli: MNV e VNT.
Questi due triangoli sono due triangoli isoscele e sono uguali. Hanno la base pari alla lunghezza dei lati del solido (1) e gli altri lati sono uguali all’altezza del triangolo equilatero unitario che compone le facce triangolari del solido (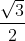
). A questo segue che VT, MN ed AB sono paralleli.
Quindi anche BT ed AV sono paralleli poiché uniscono due segmenti ( VT ed AB) paralleli ed uguali. Ne segue che esiste un piano che contiene i due segmenti. Il segmento BV, che ha un estremo sul primo ed un estremo sul secondo segmento è anche esso sullo stesso piano.
Questo ragionamento mi sembra più semplice e corregge quello che avevo inviato prima.
Per distanza tra i lati opposti del tetraedro, che utilizzavo nella risposta precedente, intendevo il segmento in verde nella figura.
Molto meglio adesso... Si ricade nel metodo di Andy, direi. Io ho usato le proiezioni, dove si dimostra abbastanza facilmente la complanarità di questo caso e la non complanarità degli altri casi. Può darsi, però, che si possa fare di meglio...