Questo articolo è stato inserito nella pagina d'archivio dedicata a Matematica e Geometria

La geometria "applicata" delle prime civiltà ci stupisce sempre di più. Probabilmente, la geometria nasce addirittura prima del linguaggio, come si può evincere anche dalla disposizione di molte strutture megalitiche.

Vi siete mai chiesti come gli Egiziani siano stati in grado di costruire le piramidi con tanta precisione? Analogo discorso si può dire anche per le costruzioni babilonesi e sicuramente anche per le culture orientali, come quella indiana e cinese. Beh... il merito più grande si deve al Nilo e alle sue esondazioni, portatrici di terra da coltivare e, quindi, di ricchezza. Non per niente tutte le grandi civiltà antiche sono sorte vicino a grandi fiumi, utili sia per il trasporto delle merci sia per il loro contributo alla più importante necessità, quella di avere del cibo.

Le inondazioni erano attese con trepidazione, ma avevano anche dei lati negativi. I confini delle zone coltivate venivano distrutte e ogni anno si dovevano tracciare le nuove linee di  confine. E, immaginiamo che, facilmente, anche allora sorgessero litigi tra vicini. Era quindi necessario utilizzare delle regole geometriche precise per non sbagliarsi e, nel caso, cercare di contrastare i soliti "furbi". In poche parole, si dovevano tracciare linee ed angoli solitamente retti. Eccoci al punto... "angoli retti".

Un angolo retto si ha quando due linee sono perpendicolari tra loro, ma dirlo è facile e costruirlo molto meno. Pensiamo, perciò, più in grande, ossia alle piramidi e alla necessità di fare in modo che lo schema di base sia esattamente formato da lati tra di loro retti. Come fare? Facile... utilizzare il teorema di Pitagora, con Pitagora che nascerà molti secoli dopo.

Com'è mai possibile? Semplice, il teorema di Pitagora era già ben noto sia in Egitto, che tra i babilonesi e sicuramente in Cina e in India. Spieghiamoci meglio... Non era conosciuto propriamente il teorema, ma l'utilizzo del legame geometrico tra i suoi lati per poter disegnare rette perpendicolari. Celebre è una tavoletta babilonese, in cui è evidente la costruzione della diagonale di un quadrato e che risale a circa 1500 anni prima di Cristo.

Ma le prime piramidi egizie sono ancora più antiche e risalgono a circa 2500 anni prima di Cristo. Ebbene sì, gli egiziani, così come altre culture, hanno da sempre utilizzato la geometria, ma per motivi molto pratici che differivano di molto da quelli greci che, invece, ne facevano qualcosa di astratto e filosofico.

Tagliando corto, arriviamo alla celebre terna pitagorica, che per il suo valore fondamentale era giudicata sacra dagli egizi. Plutarco ne dà dei legami estremamente complicati con le divinità, ma a noi interessa il risvolto essenzialmente pratico.

Consideriamo, allora la più semplice terna pitagorica: 3, 4 e 5. Ricordiamo che parlare di terna pitagorica vuol dire parlare di lunghezze  dei tre lati di un triangolo rettangolo pari a numeri interi.  Se 3 e 4 sono due cateti, 5 è l'ipotenusa. Ma, ancora più importante per fini pratici, è l'inverso, ossia il fatto che se costruisco un triangolo che abbia lati 3, 4 e 5 siamo sicuri che l'angolo tra i cateti sia retto. Nasce, così, il metodo della corda, ancora usato in certe culture contadine odierne per la divisione dei campi.

Spieghiamolo a parole e con la figura che segue...

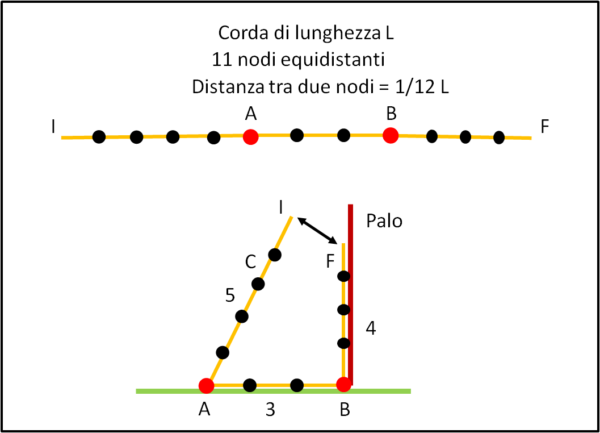
Prendiamo una corda e dividiamola in 12 parti uguali, facendo, ad esempio, 11 nodi equidistanti. Siano I e F i punti estremi della corda. Fissiamo il nodo 5 (A) al terreno, tendiamo bene la corda e fissiamo anche il nodo 8 (B). Leghiamo strettamente ciò che rimane della corda al palo che vogliamo mettere in verticale. A questo punto abbiamo le lunghezze che ci servono:

IA = 5/12 L

AB = 3/12 L

BF = 4/12 L

Ovviamente la terna pitagorica 3, 4, 5 continua a valere anche se la moltiplico o la divido per uno stesso numero, ossia i tre pezzi di corda posso scriverli come 5, 3 e 4.

Non resta che tirare bene la corda e fare in modo che I coincida con F. In questo modo, siamo sicuri di avere a che fare con un triangolo rettangolo e, quindi, che l'angolo in B (tra palo e terreno) sia proprio 90°.

Ovviamente, la stessa costruzione si può eseguire sul piano del terreno e, quindi, tracciare due rette perfettamente perpendicolari. La perfezione delle lunghezze delle piramidi (e non solo) ci dimostrano che gli egizi sapevano bene come applicare la costruzione appena descritta. Nessun esplicito riferimento a un teorema, ma la certezza di una costruzione geometria che sarà studiata per millenni.

Insomma, Pitagora ne ha un po' approfittato...