Categorie: Fisica classica
Tags: caduta libera dinamica profondità quiz voragine
Scritto da: Vincenzo Zappalà
Commenti:7
(QI) Quant'è profondo il ... pozzo? (NEW)**
I viaggi di sfruttamento minerario dei satelliti di Saturno sono iniziati. In particolare, state esplorando una voragine che si apre verso l'oceano sotterraneo di Encelado, e vi aspettate che anche con la speciale lampada che tenete in mano non ne possiate vedere la fine.
Malgrado si sappia ormai che la profondità a cui si trova l'oceano è molto minore del previsto (al massimo poche centinaia di metri, ma anche meno), non avete molto tempo a disposizione per stabilire se sia possibile scendere oppure no. Di sicuro, non oggi, dato che non avete l'attrezzatura idonea (ossia nessuna corda o apparecchiature speciali): siete praticamente a mani nude...
Riuscite a misurare la profondità d del pozzo (e come fate)?
Soluzione
Come già spiegato nei commenti, questo quiz era solo uno scherzo per vedere se qualcuno cadeva nel trabocchetto di accettare che su Encelado si potesse udire un rumore. Fabrizio e Maurizio non ci sono certo caduti e hanno smontato lo scherzo... Tuttavia, se qualcuno volesse fare i semplici calcoli, portando il tutto su un pozzo terrestre (dove il suono si propaga...) può farlo, trascurando l'attrito con l'atmosfera.
7 commenti
Mi ricorda ciò che fece chi scoprì le grotte di Frassassi, che ho visitato di recente.
La descrizione è al secondo paragrafo di questo testo:
https://it.wikipedia.org/wiki/Grotte_di_Frasassi#La_scoperta_della_Grotta_Grande_del_Vento
che ne dici Fabrizio di dirmi come fareste con qualche calcoletto?
Ci provo.
Il metodo degli speleologi di Frasassi potrebbe essere applicabile anche nel nostro caso con un paio di dubbi, credo risolti, ed un ostacolo importate.
Alla base c'è la relazione che lega distanza e tempo in un moto con accelerazione costante.
Possiamo considerare l'accelerazione costante poiché la profondità da misurare si assume sia relativamente piccola (centinaia di metri invece delle decine di km stimati attualmente).
Misurando il tempo di caduta di un qualsiasi oggetto possiamo derivare la profondità (d).
Occorre calcolare l'accelerazione gravitazionale sulla superficie di Encelado con la legge di Newton.
Il risultato è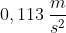
I dubbi derivano dalla vicinanza con Saturno. L'enorme massa di questo pianata ha qualche effetto sulla nostra misura?
Il nostro riferimento è Encelado che orbita intorno a Saturno. Quindi siamo in "caduta libera" su Saturno e, nel nostro riferimento, non misuriamo effetti della sua gravitazione.
In realtà ci sono le forze di marea poiché non siamo nel baricenro di Encelado. Ho provato a valutare il loro effetto. Se non ho fatto errori, le accelerazioni sono relativamente piccole rispetto ai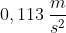
, ancora trascurabili per una misura approssimata.
Quindi, se riusciamo a misurare il tempo di caduta, possiamo stimare la profondità. Ad esempio, un tempo di caduta di 50 s corrisponde ad una profondità di circa 140 m.
Qui c'è un ostacolo importante.
Sulla Terra basta fermare il cronometro quando si sente il suono dell'impatto sul fondo del pozzo, ma su Encelado l'atmosfera che dovrebbe farci arrivare il suono è quasi assente.
Forse ci si può affidare al trasferimento del suono nella crosta gelata del satellite. Dovremmo riuscire a sentire, magari strumentalmente, la vibrazione causata dall'impatto.
Fabrizio è una vera sicurezza... e ha toccato anche il punto fondamentale: non abbiamo alcuna strumentazione speciale, siamo a mani nude...
"Forse ci si può affidare al trasferimento del suono nella crosta gelata del satellite. Dovremmo riuscire a sentire, magari strumentalmente, la vibrazione causata dall'impatto."
Mi ricordo che per sentire l'arrivo del treno da assaltare, gli indiani poggiavano l'orecchio sulle rotaie... la velocità del suono nel metallo è molto alta (circa 5000 m/s se non ricordo male) lo stesso vale nel ghiaccio e introduce un ritardo trascurabile per una stima approssimativa. Il problema è che appoggiare l'orecchio sul ghiaccio di Encelado, poi si rischia di non riuscire a staccarlo, senza contare che bisogna levare il casco. Per stare tranquillo io appoggerei il casco senza levarlo... ma cosa butto nel crepaccio? la lampada?
Beh... devo ammetterlo: volevo solo fare un piccolo scherzo e sperare che qualcuno facesse i facili calcoli della caduta di un pezzo di ghiaccio (o magari anche della lampada), tenendo conto del fatto che il suono della caduta nell'acqua ritarda il momento effettivo dell'impatto. Fatto ciò, la risposta sarebbe stata, da parte mia: "No, non si ottiene un bel niente, dato che su Encelado non si trasmette il suono". Ma voi siete subito andati oltre e non siete caduti nel tranello... cercando anzi di superare il problema. Va beh... ho scherzato, non lo faccio più...
Siete veramente rapidi e logici!
Anch'io ho pensato le stesse cose scritte da Fabrizio, magari tentando di far cadere la lampada con il proiettore rivolto verso l'alto e se, della massa totale della lampada, la maggior parte si trova sul lato opposto del proiettore, confidando in un moderato effetto dei moti rotazionali e/o oscillatori cui sarebbe sottoposta la lampada durante la sua caduta.
Ad ogni modo, con un salto di circa 140 metri, la velocità d'impatto sul fondo sarà: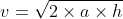
ovvero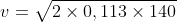
≈ 5,6 m / s che sulla Terra equivarrebbe ad un salto da un'altezza
Inoltre, se il diametro del pozzo lo permette, si potrebbe pensare di lanciarsi da un punto del pozzo verso un punto diametralmente opposto, impattando in maniera controllata e compiendo il percorso di caduta non in linea retta ma a "zig-zag", dove ogni "zigo" ed ogni "zago" smorzano la componente verticale del vettore accelerazione secondo un fattore pari al seno dell'angolo di inclinazione di ogni "zigo" sul piano di terra (anche se in realtà così facendo, ogni "zigo" ed ogni "zago" sono dei moti parabolici e non rettilinei, ma l'approssimazione potrebbe essere accettabile).
Morale della favola, si potrebbe atterrare sul fondo del pozzo con una velocità (considerando la componente orizzontale e quella verticale del vettore velocità) minore di 5,6 m / s e sarebbe pure divertente...