Categorie: Matematica Riflessioni
Tags: andata e ritorno lumaca muro versione "indiana"
Scritto da: Vincenzo Zappalà
Commenti:19
La lumaca e il muro (versione indiana) */**** (con soluzione)
Chi non conosce il vecchio quiz relativo alla lumaca e al muro che vuole scalare? Penso nessuno... Vediamone, però, una versione più elaborata, ideata da un ingegnere indiano (e sappiamo quanto siano bravi in matematica gli indiani).
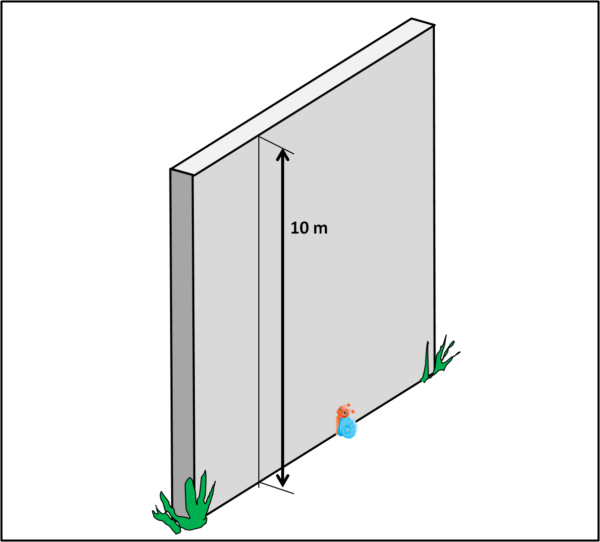
Una lumaca si trova alla base di un muro, alto 10 metri, e inizia a scalarlo. La lumaca, però, deve andare con molta calma, prendendosi anche il giusto riposo. Ne segue che essa riesce a salire di 2 metri ogni ora, ma poi è costretta a riposarsi e a dormire per un'ora. Durante il riposo essa scivola di un metro. Poi ricomincia a salire.
La classica domanda è:
Quanto tempo impiega per arrivare in cima al muro *?
Se qualcuno non conoscesse ancora il quiz, potrebbe cominciare a rispondere a questa semplicissima domanda.
Noi, invece, proseguiamo l'avventura...
La lumaca raggiunge la cima del muro, non rinuncia al suo pisolino di un'ora, ovviamente senza scivolare, dato che si trova sopra al muro, e poi decide di tornare da dove era partita. Il suo movimento è lo stesso dell'andata: scende per un'ora e poi si risposa per un'ora con tutte le conseguenze del caso. Quanto tempo totale impiega per salire e scendere dal muro****?
La matematica necessaria è irrisoria (un asterisco), ma è necessario ragionare con molta logica e un po' di fantasia "concreta".
SOLUZIONE:
Beh.. la soluzione "realistica" è stata data nei commenti da Fabry, Luigis e, in un secondo tempo, anche da Artù.
Il succo di tutto è chiedersi: "Perché la lumaca scivola?". Trascurando l'effetto bava che non so bene come e se funzioni, la causa più ovvia è la gravità. Ma se la gravità fa scendere di un metro all'ora quando la lumaca sta ferma, deve fare lo stesso anche quando la lumaca sta salendo. Il che vuol, dire che l'effettiva velocità della lumaca è di 3 metri al secondo, che si riducono a due per colpa della gravità. In discesa, allora, la lumaca riesce a esprimere tutta la sua velocità intrinseca, alla quale si aggiunge l'aiuto datogli dalla gravità. Il che vuol dire che la velocità finale della lumaca è di 4 metri al secondo. Il l'ho trovato piuttosto carino...
19 commenti
Data l'ora tarda, puo' darsi io sia caduto in qualche tranello logico.. Comunque, ci provo.
Ho diagrammato il comportamento della lumaca. In ascisse il tempo in ore, in ordinate l'altezza in metri. I tratti con pendenza positiva sono quelli in cui la lumaca sale, quelli con pendenza negativa quelli in cui la lumaca scende. Nell'arrampicata iniziale, il suo riposo è deleterio perché le fa perdere quota. Nella discesa finale, invece, continua a muoversi nella giusta direzione (in quel caso verso il basso) anche mentre si riposa. Ho inteso quel " scende per un'ora e poi si risposa per un'ora con tutte le conseguenze del caso" nel senso che anche in discesa fa 2 metri ogni ora, poi si ferma per riposare un'ora e in quest'ora scivola di 1 metro. In sintesi, mi pare impieghi 17 ore per salire in cima al muro e 24,5 ore per salire e scendere dal muro.
Mi spiace deluderti, caro Arturo Lorenzo, ma è la stessa soluzione a cui avevo pensato io e il prof. me l'ha bocciata (devi sapere che sono la sua cavia preferita per testare i quiz di media/bassa difficoltà e me li propone in anteprima, ma con scarsi risultati...
).
Potrebbe essere questa parte della soluzione.
mamma mia! un'ora di quella tiritera farebbe "scappare" anche una lumaca!!!!
Ciao Daniela, come si dice... "mal comune, mezzo gaudio"
Allora, evidentemente, non abbiamo capito correttamente qualcosa.
Ti confesso, Arturo Lorenzo (sottovoce perché non mi senta Enzone...
), che più ci penso (lo sto facendo da due giorni) più mi convinco che, date le condizioni poste dal quiz, la nostra soluzione sia valida. Perché, a mio parere, mentre la lumaca è sveglia e si muove, si oppone a quel "qualcosa" nello stesso modo sia in salita che in discesa. Ma forse mi sfugge qualcos'altro... boh, attenderò la soluzione e, nel frattempo, continuo a fare la cavia per altri "semplici" quiz, ma non ci sto cavando un ragno dal buco! Sigh 
Un dubbio mi viene in merito allo scivolamento nella fase di discesa. Quando la lumaca scende dal muro, scende per un'ora (percorrendo, si spera, 2 metri, come in salita). Poi si ferma per riposare un'ora "con tutte le conseguenze del caso". Dovrebbe cioè scivolare giù di 1 metro, come in salita ? Ma, erro o la lumaca può scivolare solo sulla sua bava ? Poiché non è ancora passata su quel metro di discesa, la sua bava ancora non c'è, quindi non può scivolare. Per cui durante il riposo in discesa rimane semplicemente ferma per un'ora e poi riprende a scendere. In tal caso impiegherebbe 27 ore tra salita e discesa. Ovviamente, non sono uno studioso di gasteropodi, quindi potrei aver pensato una cavolata. Me ne scuso con le lumache
Dai, non esageriamo... trascuriamo la bava... oppure diciamo che tutto il muro è già pieno di bava.
Comunque, Artù... potremmo poi farne una versione ancora più sofisticata! Per adesso, limitiamoci...
La soluzione credo dipenda dalle assunzioni che si fanno sul movimento della lumaca. La più semplice è quella di Arturo e Daniela che potrebbe anche essere valida non conoscendo la biomeccanica del movimento della lumaca. Una più complicata potrebbe assumere che la lumaca indiana ha un "moto proprio" uguale in discesa e salita al quale si sovrappone lo scivolamento. Scivola, scivola, scivola sempre, anche quando si muove. Con questa assunzione, se non ho sbagliato i calcoli, dovrebbe impiegare 17h per la salita + 1h di sosta in cima + 4h per la discesa.
22ore e 40 minuti?
Luigis... devi spiegare come hai ottenuto questo valore...
Ogni ora, salendo, la lumaca guadagna un metro (+2-1). Così fino alla sedicesima ora, quando, dopo il riposo, si ritrova all'ottavo metro. Nella successiva diciassettesima ora, con i due metri positivi, raggiunge la cima del muro. La lumaca riposa, e allo scoccare della diciottesima ora, inizia la discesa.
Immaginando che la gravità la faccia scivolare anche mentre scende, ad ogni ora di cammino attivo, la lumaca guadagna tre metri in discesa e poi, nell'ora di riposo, un altro metro di scivolamento. Perciò dopo 19 ore è a sette metri dal suolo; dopo 20 ore a sei metri; dopo 21 ore a tre metri e dopo 22 ore a due metri da terra. A questo punto i due metri mancanti corrispondono a due terzi di un'ora (= 40 minuti).
INVECE NO!
Se considero che ad ogni ora lei scivola un metro in giù, significa che con le sue forze, in salita farebbe tre metri ogni ora. In discesa, ai tre metri che farebbe ogni ora con le sue forze, si aggiunge il metro di scivolamento e fanno quattro metri all'ora. 4+1+4+1=10. In quattro ore la lumaca è a terra.
18 + 4 = 22 ore
E bravi Fabry e Luigis. L'importante in questo quiz è chiedersi: PERCHE' la lumaca scivola? Se è per la forza di gravità, la risposta corretta è proprio 22 ore.
Attendo, comunque, la versione arturiana che introduce l'effetto "bava" ...
La domanda mi nasce spontanea: visto che chi ha risposto , me compreso, ha ricavato lo stesso risultato per salire (17 ore) , mentre si hanno risposte diverse per la discesa, giustificate dallo scivolamento per gravità sovrapposto al movimento naturale della lumaca, allora perché nella fase di ascesa tale scivolamento verso il basso (per gravità) sovrapposto al movimento verso l'alto della lumaca non viene considerato ? Cioè, se nella fase di discesa del muro lo scivolamento per gravità sovrapposto al movimento della lumaca la fa arrivare prima alla base del muro, perché nella fase di salita non la fa arrivare dopo in cima al muro ?
Giuro che mi procurerò una lumaca farà il necessario esperimento sul muro di casa, alto esattamente 10 metri
Mi sa che ho capito: nella fase di salita il testo dice chiaramente che riesce a salire di 2 metri in un'ora, quindi tiene conto implicitamente dell'effetto "scivolamento sovrapposto al moto naturale della lumaca", cioè i 2 metri sono al netto di tale effetto. Mentre nella fase di discesa si dice genericamente che scende per un'ora, senza specificare di quanto. Lo sapevo che il tranello era in agguato , furbacchione di un Prof !
caro Artù,
viene tenuto in conto, dato che la velocità di ascesa della lumaca risente della gravità: la lumaca percorrerebbe 3 metri in salita, ma durante la salita la gravità si contrappone e lei ne sale solo 2. Quando dorme, ovviamente, gioca solo la gravità. Assumendo ora che la velocità della lumaca sia proprio di 3 metri all'ora, quando scende la gravità l'aiuta e viaggia, perciò, a 4 m/h. Quando dorme, invece, subisce solo la gravità che la fa scendere di un metro. Ti torna?
Si, come scrivevo sopra, i 2 metri percorsi in salita in un'ora tenevano implicitamente conto dello scivolamento per gravità, senza il quale, appunto, la lumaca percorrerebbe 3 metri in un'ora in salita (visto che lo scivolamento senza movimento è di 1 metro in un'ora). Capito questo, tutto torna anche in discesa.
Scusa Artù, ma ho risposto senza aver visto il commento delle 8:39...