Ancora sul paradosso dei gemelli... ma questa volta cerchiamo di chiarire la faccenda una volta per tutte. Il paradosso, che si dovrebbe chiamare più correttamente, paradosso degli orologi, rimane un esperimento mentale perfettamente in linea con le ipotesi della Relatività Ristretta.

Lo so, lo so, ne abbiamo parlato in tanti articoli (in particolare QUI) e l'abbiamo anche descritto in molti modi. Tuttavia, mi irrito sempre un po' a leggere che il celeberrimo paradosso dei gemelli  sia dovuto all'accelerazione e che quindi rientri nel campo della relatività generale. Essa è necessaria, forse, per rendere il paradosso realistico, ma il  vero scopo di Einstein nel proporlo era ben diverso ed è legato esclusivamente alla relatività ristretta (RR).

Il succo di tutto è che ancora oggi si leggono dimostrazioni, descrizioni e conclusioni che poco hanno a che fare con il paradosso originale. Il risultato è una grande confusione...

Cerchiamo di fare chiarezza una volta per tutte.

Il paradosso degli orologi

Il paradosso nella sua veste originaria ha poco a che vedere con i gemelli, dato che è stato proposto dallo stesso Einstein ben prima di descrivere la sua relatività generale. Niente accelerazioni, quindi, e nessun gemello, ma solo orologi che rispondano ai criteri della relatività ristretta. Il fatto che qualcuno lo abbia apprezzato a tal punto da volerlo rendere completamente "biologico" ha, purtroppo, causato critiche e confusione che erano ben lontane dalle intenzioni di Einstein.

Il paradosso viene sollevato da Einstein solo e soltanto per evidenziare al meglio come la relatività ristretta abbia bisogno di una comprensione perfetta per descrivere le sue conseguenze. In particolare, Einstein presenta un esperimento mentale che è basato proprio sulla caratteristica fondamentale della sua teoria: velocità costante tra sistemi di riferimento. Viene esclusa, perciò, qualsiasi accenno alla accelerazione. Ciò comporta che qualsiasi cambiamento di velocità può essere solo e soltanto istantaneo.

Solo nel 1911, un fautore della teoria del grande Alberto (Paul Langevin), si lancia in un'interpretazione biologica, introducendo i due gemelli e la loro età. Niente di male, teoricamente, ma questa presentazione ha comportato un sollevamento di critiche da parte di molti scienziati che, interpretando male la RR, vedono nell'età finale dei due fratelli, giudicata da entrambi concordemente diversa, una prova della infondatezza della teoria einsteniana, dato che essa vorrebbe, invece, dimostrare che quella che conta è la velocità relativa tra i due attori del paradosso e che, quindi, il risultato finale a favore di uno solo andrebbe contro le aspettative. In  altre parole, un sistema di riferimento sarebbe favorito rispetto a un altro... e questo è inaccettabile.

Sembra quasi impossibile che non si sia capita la vera motivazione di Einstein: un risultato apparentemente discordante con la sua teoria spiega, invece, in modo perfetto l'importanza dei sistemi di riferimento, sulla cui definizione Einstein ha basato proprio tutta la teoria (vedi esame tra Newton ed Einstein, prima di Fig.13). Purtroppo, sembra che ancora oggi la scarsa comprensione non sia cosa tanto rara.

In realtà, Einstein lo presenta come un paradosso degli orologi e non di esseri umani. Il che vuol dire che a lui interessa solo descrivere come gli orologi di due sistemi in moto relativo si vedano uno con l'altro. Il paradosso è solo e soltanto un esperimento mentale che segue perfettamente le regole della RR. In particolare, quindi, poco interessa ad Einstein il tenere in conto del modo in cui si è raggiunta una certa velocità e nemmeno come si faccia a invertire di segno istantaneamente.  Queste sono condizioni che la RR deve poter fare, dato che esclude la presenza di accelerazioni.

Prima di iniziare una attenta e particolareggiata analisi del paradosso, chiariamo alcuni concetti fondamentali.

Punti fondamentali

(1) Un sistema di riferimento è definito dall'insieme di un numero qualsiasi di orologi che segnino tutti la stessa ora (analoga definizione per i "righelli", ma il paradosso non ha bisogno di introdurre la contrazione spaziale).

(2) Due sistemi possono essere in moto relativo, ma ognuno di loro può considerarsi "in quiete", ossia fermo, e dedurre che chi si muove è l'altro sistema (su questo punto era già stato chiaro Galileo e prima di lui Giordano Bruno).

(3) Il sistema in quiete osserva che gli orologi dell'altro sistema rallentano rispetto ai suoi. Il che implica che, dato che ogni sistema può considerarsi in quiete, entrambi i sistemi  devono concludere che i loro orologi girano più velocemente. Attenzione 1! Non è certo questo un paradosso, dato che è un punto fondamentale della RR. Guai se non fosse così... Inoltre, Attenzione 2! Se un orologio rallenta vuol dire che il tempo che segna è minore. Non facciamo confusione ...

(4) Per accettare questo punto fermo, è necessario aver compreso bene non solo il rallentamento in sé, ma la sua vera causa: la non simultaneità di un certo evento nei due sistemi. Il concetto di non simultaneità è veramente essenziale e penso di fare cosa utile nel  rappresentarlo in Fig. 1. Do, ovviamente, come dato di fatto la conoscenza del diagramma di Minkowski e di come si manifesti su di esso la dilatazione dei tempi, ossia il rallentamento degli orologi del sistema, considerato in movimento, quando viene osservato da chi si considera in quiete, ossia -ancora- il fatto che il tempo segnato dagli orologi supposti in movimento appaia minore del loro, da parte di quelli che si considerano in quiete.

Il problema della simultaneità

Consideriamo due sistemi di riferimento, uno nero e uno rosso. Chiamiamo O gli orologi del primo e con O' gli orologi del secondo. Possiamo prendere uno qualsiasi di due sistemi come sistema in quiete (ad esempio, quello nero O).

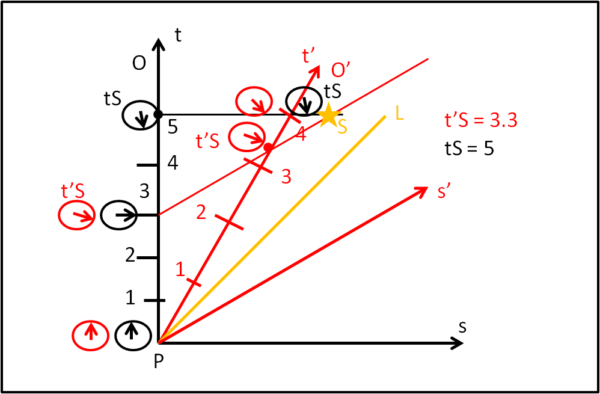
In esso, l'asse del tempo è verticale  e quello dello spazio è orizzontale. L'altro sistema O' viene visto, da O, muoversi con una certa velocità, ossia viene visto variare il suo tempo in funzione dello spazio che percorre. Ne segue che l'asse del tempo di questo sistema (rosso) è inclinato rispetto a quello del primo (è solo e soltanto la definizione di velocità ...). Rifacendoci al punto (3) disegniamo gli intervalli di tempo in entrambi i sistemi (ho messo dei numeri a caso e lascio a voi eseguire, come esercizio, un esempio calcolando il coefficiente di dilatazione gamma reale sulla base della velocità scelta).

Avendo scelto come sistema in quiete quello nero, sul suo asse segniamo le tacche unitarie che corrispondono a un certo intervallo di tempo fisso. Vicino a ogni tacca, sia lungo l'asse, sia su ogni linea orizzontale esiste SICURAMENTE un orologio  O di questo sistema. Per come  è stato definito il sistema di riferimento, tutti gli orologi neri che stanno sulla stessa linea orizzontale definiscono la simultaneità, ossia DEVONO segnare tutti la stessa ora.

Le tacche rosse relative all'asse del tempo del sistema rosso O', pari a una certa unità di misura uguale a quella del sistema  nero (ad esempio, un secondo o un anno o quello che volete), sono chiaramente più separate tra di loro, dato che nel sistema nero scelto in quiete, il tempo del sistema rosso RALLENTA. Per qualsiasi velocità si scelga (al massimo quella della luce), la separazione tra le tacche dell'unità di tempo, varia secondo il celebre parametro gamma che caratterizza la trasformazione di Lorentz (per velocità pari a quella della luce, non si riesce a segnare nemmeno una tacca, dato che praticamente gli orologi di questo sistema non si muovono affatto, se visti dal sistema in quiete nero).

Per rispettar le ipotesi della RR, dobbiamo immaginare che gli orologi di O e O' vengano sincronizzati esattamente nel punto P. In quell'istante, tuttavia, l'orologio O' del sistema rosso deve già muoversi, rispetto al sistema nero, con una certa velocità costante che non cambierà più. In altre parole, non possiamo fare partire il sistema degli O' "da fermo" (avremmo bisogno di farlo accelerare), ma dobbiamo pensare che esso stia già viaggiando a una certa velocità rispetto al sistema degli O e che gli orologi vengano sincronizzati sul valore ZERO quando passano esattamente per il punto P. E' o non è un esperimento mentale?

Come abbiamo definito la simultaneità per il sistema nero, così possiamo fare lo stesso per il sistema rosso. Tuttavia, sappiamo bene dalla rappresentazione di Minkowski, che l'asse rosso dello spazio DEVE essere anch'esso inclinato rispetto a quello nero e, precisamente, dello stesso angolo di cui è inclinato l'asse del tempo rosso rispetto a quello nero. Ne segue che le linee di SIMULTANEITA' del sistema rosso devono essere parallele all'asse dello spazio rosso: solo su queste linee gli orologi rossi segnano lo stesso tempo. Attenzione: Per gli orologi neri, gli orologi rossi girano più lenti, ma la loro simultaneità non viene certo intaccata.

Immaginiamo, adesso che esploda una supernova S. Abbiamo, cioè, introdotto un certo evento nello spaziotempo. Questo evento è del tutto indipendente dai sistemi di riferimento che abbiamo disegnato: esso accade e basta! Ciò che cambia sono, però, le sue coordinate rispetto ai sistemi di riferimento in moto relativo. Infatti, tracciamo la linea leggera nera che passa per S e portiamola fino all'asse nero del tempo. I suoi orologi e, in particolare, quelli sull'asse dei tempi, ci dicono che è avvenuto al tempo ts = 5.  Facciamo, invece, passare la linea rossa leggera per S e portiamola fino all'asse dei tempi rosso. Gli orologi O' misurano un loro tempo e l'evento corrisponde al tempo t's rosso, di poco superiore al tempo 3, ad esempio 3.3 (ho fatto una lettura molto qualitativa).

Come già detto, TUTTI gli orologi O che stanno sulla linea parallela a quella dello spazio nera, misurano lo stesso tempo e, quindi anche quello che si trova sull'asse del tempo rosso. Questo orologio è in grado di confrontare l'ora che sta misurando lui con quella che sta misurando l'orologio rosso. Deve, perciò, concludere che mentre lui registra un valore pari a ts = 5, quello rosso che si sovrappone a lui segna un tempo t = 4. Il sistema nero conclude, da questa visione diretta, che l'evento S è avvenuto al tempo t = 4 per l'orologio rosso.

Se al posto degli orologi prendiamo il battito del cuore diventa del tutto naturale passare dagli orologi all'età degli osservatori: per il sistema nero un certo evento avviene quando l'osservatore rosso è PIU' GIOVANE di lui!

Un discorso simile, però, può essere fatto anche dagli orologi rossi. L'evento, per loro, avviene al tempo t's = 3.3. Tracciando la linea leggera rossa parallela alla linea rossa dello spazio, definiamo la posizione di tutti gli orologi di O' che segnano la stessa ora (linea di simultaneità rossa). In particolare ci interessa quello che si trova proprio sull'asse dei tempi nero. Lui confronta il suo tempo con quello che legge sull'orologio nero a lui sovrapposto. Ne conclude che il suo tempo t's = 3.3 è più grande del tempo t = 3.0 segnato dall'orologio nero. In altre parole, per l'osservatore rosso, è quello nero ad essere PIU' GIOVANE.

Nota Bene:  l'aver usato tutti gli orologi dei due sistemi e non solo quello di chi viaggia o sta fermo, ci ha evitato di dover mandare dei segnali luminosi con tutte le conseguenze del caso (anche la luce viaggia a una certa velocità).

Quanto mostrato con la Fig. 1 ci dimostra chiaramente che, rispettando perfettamente le condizioni necessarie all'applicazione della RR, gli orologi di un sistema vedono quelli dell'altro girare più lentamente dei loro, ossia entrambi vedono l'altro sistema apparire più giovane. Questo, quindi, NON E' UN PARADOSSO, ma ciò che impone la RR!

Siamo, ora, pronti ad affrontare il paradosso degli orologi  e capire come si sia passati, in modo abbastanza improprio, a quello dei gemelli.

Il paradosso al microscopio

Ripetiamo esattamente la Fig. 1 in Fig. 2, dove, però, cambia  l'evento che vogliamo analizzare.

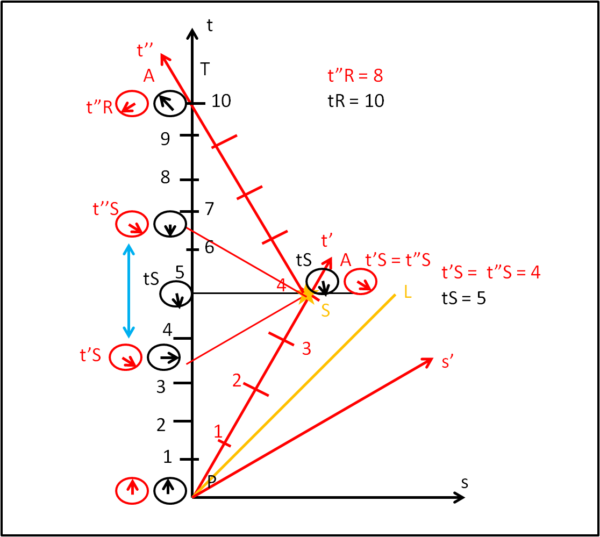
Consideriamo con O' gli orologi del sistema di riferimento di un astronave che viaggi a grande velocità vero una stella S. L'evento, adesso, è proprio il raggiungimento della stella. Utilizziamo lo stesso sistema per sincronizzare gli orologi in P, rispettando l'ipotesi fondamentale della velocità relativa costante. Anche l'arrivo sulla stella non presuppone un rallentamento e una fermata, ma un istante in cui l'astronave continui a viaggiare alla sua velocità (relativamente al sistema terrestre T con gli orologi O). Un vero e proprio "passaggio" che permetta, però, di confrontare orologi sovrapposti dei due sistemi.

Analogamente a quanto concluso precedentemente nella Fig. 1, quando l'astronave A raggiunge la stella S, dobbiamo ammettere che gli orologi di T  vedono l'astronauta A essere più giovane, ma, contemporaneamente, l'astronauta A vede invece  gli osservatori terrestri più giovani. Per l'orologio terrestre posto vicino alla stella il suo tempo 5 è maggiore di 4 misurato dall'orologio di A, ma l'orologio di A posto sull'asse temporale della Terra, vede il suo 4 maggiore di quello segnato dall'orologio terrestre, ossia 3.5.  

In S, l'astronave A inverte la direzione del viaggio, ma NON cambia la sua velocità relativa rispetto a T (la velocità ha lo stesso modulo di prima, ma verso opposto). Invertire la direzione vuole anche dire cambiare drasticamente l'asse del tempo che diventa ora t". Il viaggio di ritorno deve essere uguale e identico a quello dell'andata, ma, questa volta, eseguito in senso inverso. Ancora una volta, però, NON dobbiamo pretendere che l'astronauta A si fermi quando torna sulla terra T, ma deve soltanto confrontare il suo orologio con quello terrestre. Questo è un requisito fondamentale per rimanere, come voleva Einstein, nella relatività ristretta. La velocità relativa deve essere sempre costante e non può azzerarsi!

Ricapitoliamo i risultati dell'andata: per T l'evento "arrivo di A sulla stella S" avviene al tempo tS = 5, ma legge sugli orologi di A un tempo nettamente minore, pari a 4. Tuttavia, sappiamo anche che per l'astronauta A il tempo da lui impiegato è di 4, ma lui legge sugli orologi neri un tempo pari solo a 3.5.

Nel ritorno, poco cambia per l'osservatore terrestre. Lui sa che l'astronauta ha compiuto il viaggio di andata nel tempo uguale a 4 e alla fine non può che leggere sull'orologio dell'astronauta un ulteriore tempo uguale a 4. Il tempo totale tR per il terrestre  è  di 10, mentre osserva che per l'astronauta è stato soltanto di 4 + 4 = 8. Se preferite passare ai gemelli, possiamo dire che il gemello vagabondo ha decisamente un'età inferiore di quello sedentario! Questo risultato parziale rientra perfettamente nelle attese della RR: chi viaggia a grande velocità viene visto più giovane da chi non si è mosso per niente.

Il vero paradosso nasce, però, analizzando il viaggio di ritorno misurato dall'astronauta. Lui, all'andata, si è considerato correttamente più vecchio di quello terrestre, dato che per lui è il terrestre che si muove. Però nell'istante esatto in cui arriva sulla stella S  INVERTE la rotta e, in tal modo, cambia istantaneamente anche la direzione dell'asse del tempo e, di conseguenza anche quello dello spazio, ossia cambia istantaneamente la sua linea di simultaneità. La sorpresa ce l'ha controllando il suo orologio con quello terrestre. Ciò può farlo tranquillamente attraverso il suo orologio sovrapposto a quello terrestre posto sull'asse nero. Accidenti, non può che dire che il suo orologio è quasi miracolosamente diventato più veloce! Infatti adesso segna un tempo nettamente inferiore a quello nero, 4 contro 6.5! Cosa è successo? Il confronto che appariva corretto (4 contro 3.5) è cambiato improvvisamente in un 4 contro 6.5.

Ormai tutto è deciso... quando l'astronave arriva a sorvolare la Terra, l'orologio terrestre indica giustamente che per lui è passato il tempo tR = 10 contro un tempo t''R = 8, ma anche l'orologio dell'astronauta è costretto ad ammettere che il suo tempo t''R = 8 è veramente minore di quello del terrestre pari a 10. Il paradosso è stato causato da quel salto improvviso che vi è stato quando t'S è diventato t"S. Mentre l'orologio rosso non mutava l'ora segnata, quello della Terra è stato costretto a girare normalmente.

La risposta è ovvia: il salto "anomalo" (chiamiamolo pure "paradossale" ) si è avuto perché l'astronauta, al suo arrivo su S, ha invertito la rotta e, quindi, ha cambiato improvvisamente e in modo drastico il suo sistema di riferimento. Il terrestre, invece, ha sempre mantenuto il suo sistema!

Conclusioni

A questo punto, diventa fondamentale il fatto che Einstein ha chiamato il paradosso col nome di paradosso degli orologi.  Considerando solo loro ha potuto, senza problemi, accettare il salto temporale. E' o non è solo un esperimento mentale?

Ben diversa è  la situazione quando si cerca di passare a una situazione "biologica". Non tanto per il cambiamento di rotta, in fondo, dato che si può pensare non a un vero salto, ma a una curva attorno alla stella S in cui prima si rallenta e poi si accelera di nuovo, ma per il fatto che si vuole imporre che il gemello viaggiatore parta proprio dalla Terra e, soprattutto, arrivi proprio sulla Terra.  E' stata, perciò, inserita l'accelerazione e la decelerazione che ci porta fuori dai limiti della RR. In realtà, le cose non cambiano di molto, ma la situazione ha creato un mucchio di confusione del tutto inutile.

La vera situazione, con tanto di gemelli "reali", dovrebbe essere, in qualche modo, simile a quella di Fig. 3. In fondo, teniamo presente che la RG utilizza i risultati della RR su intervalli di tempo infinitesimi...

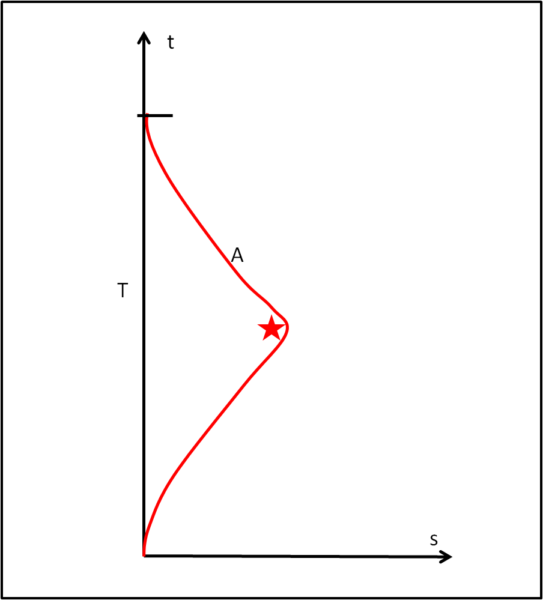
N.B.: Il modo migliore per far rimanere l'esperimento mentale perfettamente nell'ambito della RR, pur dandogli un valore di concretezza, sarebbe quella di utilizzare un terzo gemello, già in rotta verso la Terra, fin dalla partenza di A. Esso arriverebbe sulla stella S, esattamente nell'istante in cui vi giunge l'astronave A, pur avendo la direzione giusta per tornare verso la Terra. Ovviamente, però, dovrebbe sincronizzare il suo orologio con quello dell'astronauta in arrivo, al passaggio sulla stella... Ancora una volta questo problema sarebbe risolto lavorando solo con gli orologi, che possono essere sincronizzati da chiunque, ma sarebbe ben più difficile con gli orologi biologici, dato che sincronizzare l'età di due viaggiatori sarebbe molto meno realistico.

Per concludere: il paradosso dei gemelli è un esperimento mentale perfettamente riuscito nell'ambito della RR e non è un vero paradosso, ma un semplice cambiamento di sistema di riferimento. Non ne abbiamo, infatti, solo DUE, ma TRE. Mentre la Terra mantiene il suo suo, l'astronave è costretta a cambiarlo. Questo è quello che volva mostrare Einstein che, d'altra parte, l'ha proposto ben prima di formulare la Relatività Generale! La grande confusione, che ancora -purtroppo- rimane, è stata causata da chi avrebbe voluto renderlo troppo "realistico".

Teniamo conto, infine, che entrando nell'ambito della RG il paradosso dei gemelli (partenza da fermo, giro attorno alla stella e ritorno a Terra) continua a essere praticamente valido.