Questo articolo è inserito nella sezione d'archivio Onda su onda

 

Iniziamo a descrivere le nostre onde. Come già detto l'argomento è immenso, dato che il trasferimento di energia (o di informazione) utilizza, nel Cosmo, questo fantastico metodo. E' un po' come se riuscissimo ad avere contatti con chiunque, evitando qualsiasi spostamento reale. Al limite, basterebbe agire con una certa perturbazione "locale" per renderla di dominio  pubblico.

Le onde vengono divise in svariate categorie, ciascuna delle quali ha le sue caratteristiche più o meno "personali". Dovessimo trattarle  seguendo le varie suddivisioni non finiremmo mai. Limitiamoci, perciò, a descrivere i concetti fondamentali che sono largamente generalizzabili, lasciando a ciascuno le basi necessarie per andare più a fondo. La divisione più evidente riguarda il mezzo che si utilizza per il trasferimento. Noi abbiamo voluto pensare a un qualcosa che coinvolga sia la materia che il "vuoto" e abbiamo preferito proporre le onde meccaniche come onde del macrocosmo e quelle elettromagnetiche come onde del microcosmo, pienamente coinvolto, quest'ultimo, nella "strana" meccanica quantistica.

Onde del macrocosmo o onde meccaniche.

Queste sono quelle che chiunque può vedere o "sentire" attorno a lui. Esse possono essere uni, bi o tridimensionali; possono essere longitudinali o trasversali; Il mezzo utilizzato è estremamente vario e va dalle sostanze solide, a quelle liquide e a quelle gassose. Le più note sono le onde del mare, quelle del suono, quelle sismiche, ma i fenomeni collegati sono estremamente vari e, a volte, del tutto inaspettati.

A questo punto, sembrerebbe tutto abbastanza banale... ma, forse, non è così. Abbiamo veramente capito cos'è un'onda? Che cosa si intende per sua velocità? Cosa si intende per trasferimento di energia? Che cosa si intende "disturbo"?

Velocità di un'onda.

Questa è una caratteristica veramente fondamentale. Abbiamo parlato di "trasferimento" di energia e quindi è ovvio che giochi un ruolo importantissimo stabilire come  si muova questa energia. Immaginiamo che essa sia un regalo da consegnare a qualcuno. E' o non è decisivo sapere quanto tempo impiegherà il pacco ad arrivare a destinazione e che percorso farà? Tutto ciò indipendentemente dal regalo in sé. Affrontiamo quindi il concetto di velocità, imponendo che il regalo si muova, senza, però, implicare il moto di nessuno. Pensiamoci bene... Non è un problema da poco, anzi... addirittura, sembrerebbe andare contro le leggi della fisica più elementare.

Non possiamo, perciò, accontentarci di definire, in qualche modo, certe caratteristiche dell'onda, come  lunghezza  e  frequenza, e poi  descrive la sua velocità attraverso una loro semplice relazione. Riporto un tipico esempio di definizione della velocità di un'onda tratta da un testo divulgativo: "la velocità con cui l'oscillazione si sposta nella direzione di propagazione. ... questo valore è il rapporto di proporzionalità inversa che esiste tra la frequenza e la lunghezza." Tutto chiaro? Assolutamente no. Si continua a girare attorno al problema senza affrontarlo veramente.  Noi vogliamo, invece, partire proprio da "zero" e far comprendere il concetto essenziale di un'onda. Per far ciò è necessario costruirla punto per punto e istante per istante. Abbiamo detto "punto per punto" e "istante per istante". Eh sì, ancora una volta, è essenziale fare entrare in gioco sia lo spazio che il tempo, legandoli tra di loro. Qual è la grandezza che li lega meglio in fisica elementare? Presto detto, la velocità. Partiamo, quindi, proprio da lei e che i più bravi non si arrabbino...

Premessa

Quanto andremo a trattare nelle prossime righe sembrerà a molti un qualcosa di inutile: tutti sanno cos'è lo spazio e il tempo, così come la velocità che non è altro che lo spazio percorso in un certo tempo. Tuttavia, quando si descrive un'onda è necessario parlare di percorso spaziale e di percorso spaziotemporale e ne conseguono figure del tutto simili che li descrivono. Mi sono accorto che molte persone rimangono un poco confuse e mischiano una rappresentazione con l'altra. Aggiungendo, inoltre, il fatto che quando si parla di onda non vi è nessun punto materiale che veramente si muova lungo una certa coordinata; il parlare di velocità di un'onda rischia, perciò, di diventare un problema di non immediata comprensione.

Percorso e consegna di un regalo

Percorso da effettuare e consegna di un "regalo" sono due fasi, apparentemente diverse, ma strettamente legate tra loro. Il percorso individua il tragitto "spaziale" che si deve percorrere; la consegna, invece, ci indica in che modo si effettua il percorso, coinvolgendo pesantemente il "tempo" necessario a percorrerlo. Il tutto dà luogo a un movimento.

Consideriamo, ad esempio, il tragitto necessario per andare da una città O ad un'altra F per mezzo di un automobile, trasportando, appunto, il regalo. Per visualizzarlo perfettamente, la cosa migliore è sempre quella di utilizzare una cartina geografica, dalle caratteristiche puramente spaziali, e  tracciare su di essa il percorso più idoneo per ottenere lo scopo. Con questa rappresentazione spaziale, si può poi partire da O con l'auto C procedendo con una velocità costante. Ripetiamo, OF è il percorso segnato sulla cartina; il variare dello spazio con il tempo ci indica come viene effettuata la consegna; la macchina C è il mezzo che viene utilizzato.

Disegniamo la banalissima Fig. 1, dove in alto a sinistra è rappresentata la nostra cartina stradale.

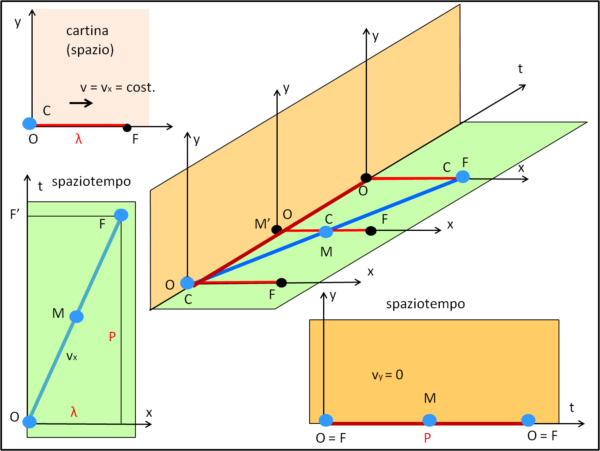
Siamo fortunati: la città O di partenza e la città F di arrivo sono collegate da una strada perfettamente rettilinea, sulla quale poniamo subito il nostro asse x. Inclinato di 90°, disegniamo anche l'asse y, anche se in questa avventura non ci servirà molto (ovviamente, trascuriamo le salite o le discese, altrimenti saremmo obbligati a introdurre anche l'asse z e il problema sarebbe molto più complicato). Abbiamo tutto il necessario a descrivere il nostro viaggio? In realtà no. Per visualizzarlo completamente dobbiamo introdurre anche il tempo: solo lui, infatti, ci permette di vedere perfettamente come si svolge il viaggio, istante per istante. In questo semplicissimo caso, potremmo anche eliminare l'asse y e utilizzare il ben noto diagramma spaziotemporale, in cui le coordinate sono lo spazio (asse x) e tempo (asse t), ma noi ci vogliamo complicare le cose e inserire in un'unica figura a tre dimensioni sia il percorso sulla cartina (x,y) sia il modo in cui si effettua ((x,t) e (y,t)). La parte centrale della Fig. 1 riporta proprio questo diagramma spaziotemporale, con i tre assi x, y e t.

Al tempo t₀ l'auto C parte da O. si  muove sia lungo l'asse x che lungo l'asse del tempo t e giunge a metà strada M, infine arriva in F e si può consegnare il regalo.

La retta azzurra riporta in modo esauriente il movimento spaziotemporale dell'auto C. Può essere utile (per situazioni più complesse) proiettare questo movimento sia sul piano (x,t) che sul piano (y,t). Nel primo caso abbiamo la retta OF che abbiamo appena evidenziato. L'inclinazione di questa retta (o, meglio, segmento di retta) indica la velocità dell'automobile, dato che ci dice istante per istante il rapporto tra spazio percorso (lungo l'asse x) e il tempo impiegato a percorrerlo. Nel piano (y,t) abbiamo invece un tragitto solo temporale, ossia l'auto non si muove assolutamente e, infatti, l'inclinazione del "movimento" è pari a zero, ossia avviene a velocità nulla (la macchina è ferma rispetto all'asse y).

Attenzione, quindi, a non confonderci... Il tragitto rosso è solo spaziale e indica il tragitto da compiere sulla cartina, mentre il tragitto azzurro avviene nello spazio-tempo a 3 dimensioni (x,y,t) e descrive il moto dell'auto C istante per istante durante il suo spostamento da O a F.

Prima di lasciare la Fig. 1, diamo qualche "nome". Chiamiamo λ lo spazio percorso lungo l'asse delle x (che, in questo caso, coincide esattamente con il percorso effettuato dalla macchina) e con P l'intervallo di tempo trascorso tra la partenza da O e l'arrivo in F. Possiamo tranquillamente dividere lo spazio per il tempo e ottenere la velocità dell'auto C, dato che essa è stata scelta come costante.

v = v_x = λ/P

Teniamo bene a mente questa banalissima, ma fondamentale formula.

Nella consegna precedente abbiamo usato come MEZZO di trasporto un'auto. Possiamo chiederci: "La macchina C ha trasportato solo il regalo o anche qualcos'altro?". Molte cose (guidatore compreso), ma, in particolare, un "pacchetto" di energia, avendo sia una massa che una velocità (energia cinetica, ossia di movimento, K = 1/2 m v²). Se non ci credete provate a mettere un muro davanti alla macchina e vi accorgerete del disastro!

Una palla di cannone

Di questi terribili tempi potremmo anche cambiare il mezzo di trasporto e anche il tipo di regalo. Ad esempio, potremmo usare un cannone e una palla di metallo lanciata dal cannone. Per recapitare questo tragico regalo sappiamo bene come fare... Qual è, adesso, la "cartina" geografica? Beh, sempre la stessa, ma il tragitto da compiere non è più un segmento rettilineo, ma un tratto di parabola. La nuova strada da O ad F ha un andamento curvilineo, ossia coinvolge sia l'asse x che l'asse y, entrambi puramente spaziali. Quanto detto lo vediamo nella parte alta a sinistra di Fig. 2.

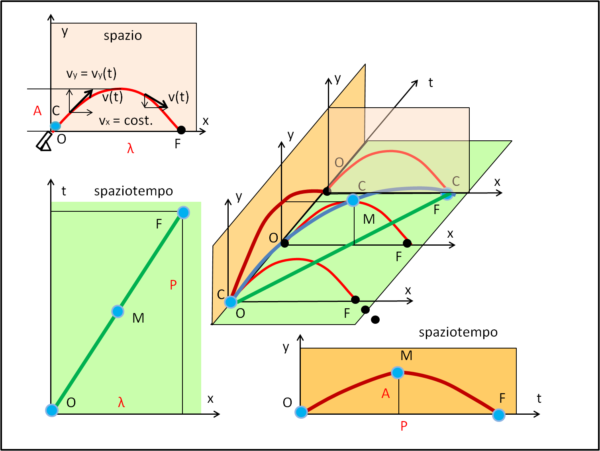
In modo analogo  a quanto fatto precedentemente, disegniamo, nella parte centrale, la traiettoria spaziotemporale della palla di cannone C. Essa è data dalla curva azzurra. Come prima, possiamo proiettare questo "movimento" sia sul piano (x,t) che sul piano (y,t). Sappiamo anche che la palla di cannone ha una velocità variabile da istante a istante e, per adesso, poco ci importa che questa variabilità sia dovuta alla gravità terrestre. In realtà, la componente della velocità secondo x rimane costante, come nel caso di Fig. 1, ma non la v_y che varia istante per istante. Cosa ne segue? Che anche la traiettoria spaziotemporale proiettata sul piano (y,t) disegna una parabola. Utilizziamo un nuovo termine per la lunghezza massima di cui si è spostata l'ordinata della palla di cannone:  ampiezza A.

La curva percorsa nel tempo è una parabola, ma non differisce molto dalla forma di un'onda... tuttavia, non saltiamo subito a conclusioni sbagliate. Il mezzo utilizzato per mandare il nuovo "regalo" è stato una palla di cannone (stimolata in questo dallo sparo del cannone) e lei si è realmente mossa nello spazio, sia lungo x che lungo y. No, non abbiamo ancora ottenuto quello che volevamo.

Tornando alla Fig. 1, avremmo anche un'ulteriore possibilità per trasportare il regalo senza usare la macchina. Un modo, però, non certo rapido e fattibile... Potremmo sistemare tante persone lungo il percorso spaziale OF e poi fare scorrere il regalo da uno all'altro. In tal modo, nessuna persona si muoverebbe e il regalo verrebbe comunque recapitato. Ottima idea? Come già detto, teoricamente ottima, ma praticamente impossibile! Non solo per il numero di persone coinvolte, ma anche per il fatto che convincerle tutte a eseguire lo stesso gesto (prendi il regalo, girati e consegnalo alla persona più vicina) sarebbe sicuramente impossibile. Senza dire che qualcuno potrebbe anche pensare di prendere il regalo e scappare... Tuttavia, questa impossibile operazione ci mette già sulla buona strada.

L'importante è, ora, scegliere il tipo di regalo. Invece di inviare qualcosa di materiale, potremmo limitarci a mandare un regalo ... energetico, ossia far viaggiare da O a F soltanto un pacchetto di energia che sarebbe, comunque, un bel segnale, una informazione fondamentale.  Abbiamo già visto che sia la macchina che la palla di cannone portano con loro una bella quantità di energia, qualcosa che è basata soprattutto sulla velocità di spostamento (dove la palla tocca qualcosa di solido gli effetti energetici si vedono molto bene). Però, però, non vogliamo spostare nessuno lungo la traiettoria che va da O a F e quindi siamo costretti a far viaggiare "da sola" l'energia. Come possiamo fare?

Cambiare completamente il mezzo e affidarci veramente a una serie continua di persone che occupano lo spazio "fisico" tra O e F. In particolare, ci basta e avanza far viaggiare l'energia lungo l'asse x, quella che indica chiaramente la distanza da percorrere (λ). Se poi sapessimo anche misurare il tempo impiegato dallo spostamento dell'energia ricaveremmo la velocità dell'energia, ossia dell'informazione, il regalo inviato.

Costruiamo la "ola"

Bene, spostiamoci in uno stadio e fotografiamo la tribuna. Ciò che vediamo è una fila continua di persone, sedute una a fianco dell'altra (senza nemmeno averle dovute scongiurare di farlo). Chi è seduto all'estremità sinistra sia l'individuo O e l'ultimo a destra sia l'individuo F. Ciò che vogliamo fare è informare F di qualcosa che vuole fargli sapere O. Questa informazione deve essere solo un trasferimento di energia.  No, no, non utilizziamo il telefono senza fili, che sembrerebbe anche funzionare, dato che la frase da riportare diventerebbe rapidamente incomprensibile. Dobbiamo inviare qualcosa che rimanga sempre la stessa (almeno in prima approssimazione). Facciamo, allora uno "zoom" su O e sui primi due tifosi alla sua sinistra. Per essere sicuri che collaborino usiamo un espediente: leghiamo tra di loro i polsi, a due a due, con una corda resistente e piuttosto corta, come mostra la Fig. 3 in alto.

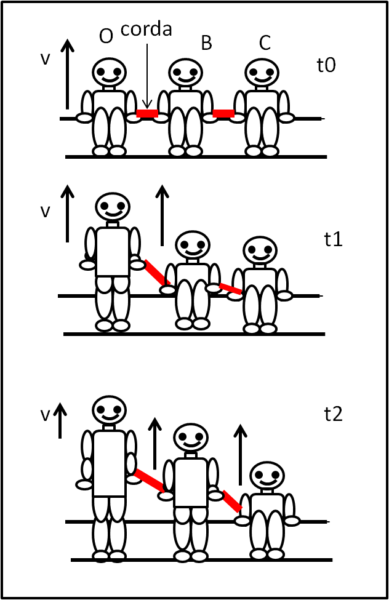
Poi diciamo ad O di fare un semplice gesto senza assolutamente muoversi verso F: quello di alzarsi in piedi e di sedersi nuovamente. In tal modo viene generato, comunque, un pacchetto di energia, dato che alzarsi e abbassarsi implicano una certa velocità, anche se limitata a una singola posizione spaziale dell'asse x. Lo spostamento dalla posizione seduta a quella eretta la chiamiamo ampiezza A (un qualcosa che abbiamo già utilizzato). Il percorso spaziale da O a F, lungo l'asse x, possiamo tranquillamente chiamarlo λ.

Bene, non ci resta che far muovere l'energia... e, quindi, passare, a una rappresentazione spazio temporale. Potremmo disegnare il solito diagramma a tre dimensioni, ma ormai sappiamo come trattarlo, e quindi possiamo, per adesso, limitarci al diagramma spaziale negli assi x e y. Ovviamente, l'ampiezza dell'oscillazione di O si misura lungo l'asse y. A intervalli di tempo regolari fotografiamo la tribuna con i suoi tifosi.

Tutto pronto? Sì? Bene, diamo il via al tifoso O. Al tempo to inizia il suo movimento verso l'alto. In t1 raggiunge una certa posizione lungo y. Una posizione questa, però, che porta la corda che lo lega al tifoso B a tendersi al massimo, In t2, infatti, anche B è costretto a seguire il movimento di O, anche se un po' ritardato. Nello stesso istante comincia a tirare anche la corda che lega B con C e anch'egli è costretto ad alzarsi. Questa sequela di "fotografie" effettuate allo spazio in tempi diversi, l'abbiamo rappresentata  in Fig. 3, con il tempo che scorre verso il basso.

O si alzerà al massimo e poi inizierà nuovamente a sedersi. A causa della corda, lo stesso movimento lo farà anche B, C e via dicendo. Rappresentiamo la tribuna dello stadio nel suo insieme, indicando sia O che F. Ancora una volta le foto vengono fatte a intervalli di tempo regolari. Ciò che capita lo riportiamo in Fig. 4.

Si vede chiaramente come i movimenti regolari dei vari tifosi creino un po' alla volta una forma che somiglia a quella di un'onda. Ad un certo istante O torna seduto. In quello stesso istante è costretto a mettersi in movimento il tifoso F. Blocchiamo tutto! Si è formata una magnifica onda spaziale tra O e F, un'onda, però, in cui nessun punto si è spostato lungo l'asse x, dato che ogni spettatore è sempre rimasto fermo al suo posto, oscillando soltanto in y. Ciò non toglie, però, che F senta la tensione della corda e, in qualche modo, si accorga che è stato raggiunto dal primo pacchetto di energia, quello dovuto all'inizio del movimento verso l'alto di O. Questa informazione ha quindi viaggiato da O a F in un  tempo ben quantificabile che possiamo tranquillamente chiamare P. Ma, ma... sappiamo quanto spazio ha percorso l'energia (λ) e adesso abbiamo misurato anche il tempo impiegato perché parta da O e arrivi in F (P).

Il periodo P, perciò,  è l’intervallo di tempo in cui viene compiuta un’oscillazione completa.

E', perciò, immediato calcolare la velocità dell'informazione, ossia dell'energia:

v = λ/P

Una velocità facilmente calcolabile che, però, non ha visto nessun tifoso spostarsi da O verso F. Proprio quello che volevamo ottenere!

Ma c'è di più... L'onda non si ferma quando si inizia a muovere F, dato che F fa sollevare il tifoso a lui vicino e via seguendo. Tutta l'onda si sposta verso destra e torna a formarsi perfettamente quando F torna a sedersi. Avrà ovviamente coperto un altro spazio λ, nello stesso intervallo di tempo P. A questo punto possiamo tranquillamente chiamare λ come LUNGHEZZA DELL'ONDA e P come PERIODO DELL'ONDA. Il periodo è infatti anche il tempo impiegato dall'onda per percorrere una distanza uguale alla lunghezza d’onda. In realtà, l'energia trasmessa non è solo lo strattone che un tifoso esercita su quello successivo, ma tutta l'onda che si crea e che si sposta lungo l'asse x (le zone colorate in rosa e azzurro). il pacchetto è un vero e proprio "pacco" di energia che si muove con velocità v lungo x. Infatti, F continua a ricevere strattoni , prima per alzarsi e poi per sedersi, per TUTTO il periodo di tempo P. Ogni spettatore viene colpito e partecipa alla formazione e al trascinamento dell'onda: il regalo viene ricevuto dal tifoso precedente e consegnato a quello successivo

Ricordando la Fig. 1 e soprattutto la Fig. 2, possiamo disegnare finalmente, in Fig. 5, il diagramma tridimensionale (spaziotemporale) che descrive il percorso da compiere e la consegna del regalo energetico. Non spaventatevi e seguite attentamente i vari grafici.

Ogni tifoso (pallina) ha un colore diverso per far notare come nessuno di essi si muova mai lungo x. Abbiamo, invece un'onda azzurra nello spaziotempo (y,t) dato che ogni tifoso si muove realmente lungo quest'asse. Non esiste, invece, un viaggio spaziotemporale lungo l'asse x (linea tratteggiata verde) e nemmeno un viaggio reale azzurro nello spazio tridimensionale (x,y, t). Il percorso spaziotemporale completo di ogni singolo tifoso, mostrato nella parte centrale,  viene rappresentato dalle linee colorate (azzurra, gialla, arancione, nero, viola). Si nota molto bene che il tifoso viola è sempre restato fermo nel periodo P e inizia a muoversi proprio al compimento del periodo, dando inizio a una nuova onda.

La proiezione nel piano spaziale (x,y) NON descrive il percorso da compiere, come nel caso dell'auto o della palla del cannone, ma descrive una specie di cartina "dinamica", in quanto nessuna pallina (tifoso) si muove realmente lungo x, ma solo lungo y. Essa descrive il percorso che compie l'energia. Notiamo che la pallina azzurra si è alzata completamente (pallina tratteggiata) ed è tornata a sedersi; quello gialla si è alzata e sta scendendo; quello arancione si trova in piedi, proprio mentre quella azzurra si sta sedendo; quella viola è sempre stata ferma e inizia ad alzarsi proprio quando quella azzurro torna a sedersi. Nel piano (x,t) vediamo chiaramente che le palline non si muovono nello spazio, ma solo nel tempo, ossia sono ferme rispetto all'asse x. Nel piano (y,t) si vede invece  come le singole palline si muovano lungo y di un moto uguale per tutte, ma sfasato rispetto al tempo.

Qualcuno dirà: "Perché complicare le cose semplici?". In realtà, posso assicurarvi che se si comprendono questi grafici, le onde e il  loro moto non avranno più segreti!

La prossima volta analizzeremo molto meglio il "movimento - non movimento" dell'onda, magari con l'aiuto di qualche formuletta. Per adesso, estendiamo il concetto di onda e di mezzo con cui si propaga. Nel caso della nostra OLA da stadio abbiamo considerato come mezzo di propagazione proprio i tifosi legati tra loro da una corda molto resistente. Nella realtà il mezzo può essere alquanto variabile: il mare, l'aria stessa o una corda. In questi casi REALI i singoli tifosi non sono altro che le particelle di acqua o d'aria o del materiale di cui è fatta la corda che vengono tenute insieme dal legame chimico e fisico del materiale (solido, liquido o gassoso) e dalla sua capacità di reagire a un certo stimolo. Nel caso della "ola" il disturbo iniziale è stato proprio il primo tifoso che si è alzato, ma, nel caso del mare, la sorgente dell'oscillazione è invece la caduta di un sasso, così come nel caso dell'aria può essere un grido o l'oscillazione di una corda della chitarra o l'esplosione di un ordigno. Sarà poi l'acqua o l'aria o molti altri "mezzi" che inizieranno la danza mediante le loro capacità elastiche. O, magari, qualcosa che per adesso viene descritta solo con la matematica o, addirittura, o è la stessa struttura dello spaziotempo. Ma ne parleremo meglio in seguito. Vedremo anche che la velocità del "pacchetto" d'energia può diventare molto grande, addirittura la massima possibile, quella della luce. Ma, in questo caso, dovremo passare al microcosmo.

(continua)