La serie completa "Dall'Atomo alle stelle e viceversa" è disponibile QUI

 

Quantizziamo tutto!

Il modello di Bohr, ancora legato a una visione classica, riesce a descrivere molto bene l’atomo più semplice, quello in cui vi è un solo elettrone e un solo protone (idrogeno). In queste condizioni si può applicare il secondo principio della dinamica (F = ma) all’elettrone di carica unitaria e e di massa m, considerando come forza quella coloumbiana fra nucleo positivo ed elettrone negativo (di pari carica). Ricordando che nel moto circolare uniforme a = v²/r, con banali passaggi matematici si arriva a una formula molto importante:

r = n²h²/4π²me² = n² r₁

espressione nella quale non compare più la velocità dell'elettrone e che mostra come risultino quantizzati anche i raggi delle orbite dell'elettrone dell'atomo di idrogeno corrispondenti ai possibili stati stazionari. Infatti, tutte le grandezze che compaiono sono delle costanti, tranne il numero n.

Inserendo i valori corrispondenti alle varie grandezze in gioco, si ottengono i raggi di tutte le orbite ammesse per l’elettrone dell’atomo di idrogeno, utilizzando come unità di distanza il nanometro (nm, pari a un milionesimo di millimetro):

n = 1      r₁ = 0.053 nm

n = 2      r₂ = 2² 0.053 = 0.212 nm

n = 3      r₃ = 3²  0.053 = 0.477 nm

…

Teoricamente un atomo “finisce” quando n va all’infinito. In modo analogo a ciò che fa l’attrazione gravitazionale. Tuttavia, per certi valori l’elettrone è praticamente libero e subisce le interazioni con gli altri atomi. Non solo, però... Nessun atomo può occupare orbite che superano un certo valore di n. Ne risulta che, in pratica, ogni atomo ha una sua energia di ionizzazione, ossia tale da farlo scappare dall'attrazione del nucleo. Per arrivare a questi calcoli bisogna, però, fare molta più strada... Teniamo, infine, conto che la posizione di un elettrone ha una sua probabilità di essere ottenuta (come ci dice la meccanica quantistica) e quindi un elettrone si trova con altissima probabilità solo molto vicino al suo nucleo. Insomma, non fatevi spaventare da numeri che portano a raggi infiniti e a energia nulle.

Trafficando con le solite relazioni si può anche scrivere l’espressione che descrive l’energia relativa a ogni orbita ammessa. In altre parole, si vede che anche l’energia è quantizzata secondo la formula:

E = -2π²me⁴/n²h² = E₁/n²

Variando n (l’unica variabile) si ottengono i valori delle diverse energie. Non fatevi ingannare dal fatto che al crescere di n l’energia sembra diminuire. Ricordatevi che c’è il segno meno davanti. Un valore negativo di un numero sempre più piccolo aumenta il proprio valore che si avvicina sempre più allo zero. Un po’ come nell’energia potenziale dovuta alla gravità. Più si va lontano dalla massa centrale, e maggiore è l’energia potenziale che, essendo negativa, tende a zero (valore massimo) per una distanza infinita. Per valori crescenti di n, però, l’energia cresce sempre di meno (ossia i gradini superiori si raggiungono con poca energia in più) e quindi non è difficile far saltare l’elettrone fuori dall’atomo se ne assorbe troppa (effetto fotoelettrico).

Per energia che tende a zero, si ottiene il fenomeno della ionizzazione, che ormai conosciamo molto bene e l’atomo è libero di viaggiare da solo.

Da quanto detto, il succo dell’atomo di Bohr è piuttosto semplice. Poiché l'elettrone dell'atomo di idrogeno può possedere soltanto i valori di energia definiti dalla precedente equazione, se si fornisce energia all'elettrone che si trova ad esempio sullo stato stazionario caratterizzato da n = 1, essa potrà essere assorbita dall'elettrone solo se è sufficiente a farlo saltare dal primo stato stazionario a uno successivo. Se non si ha la giusta forza è inutile provare a saltare sul gradino più alto!

L'elettrone eccitato tende poi a tornare spontaneamente nello stato di minore energia (n=1) riemettendo di nuovo, sotto forma di radiazione, l'energia che ha assorbito.

Facciamo l’ultimo passetto e cerchiamo di determinare a quali frequenze l’atomo di idrogeno può emettere. In altra parole, cerchiamo le frequenza delle ormai celebri righe spettrali relative all’atomo di idrogeno, ossia le sue “impronte digitali”. Basta ricordare la solita formula di Planck-Einstein che lega energia e frequenza (la base della meccanica quantistica):

E = hν

Questa formula ci dice che una radiazione possiede una certa energia che va a pacchetti e non in modo continuo. Per ottenere un pacchetto di un certo valore si deve usare una ben determinata frequenza. Nota l’energia, quindi, è immediatamente nota anche la frequenza corrispondente. In poche parole, per fornire all'elettrone energia è necessario servirsi di una radiazione di frequenza opportuna.

Nel passaggio dell'elettrone dell'atomo di idrogeno da uno stato eccitato, con numero quantico n₂ ed energia E₂ ad uno stato di minore energia con numero quantico n₁ < n₂ ed energia E₁ < E₂, si ha un’emissione di energia sotto forma di radiazione con frequenza che si scrive:

ν = (E₂ – E₁)/h

A questo punto basta, nuovamente, trafficare un po’ con le formula precedente, relativa all’energia, e si ottiene:

ν = (E₂ – E₁)/h = (2π²me⁴/h³) (1/n₁² – 1/n₂²)

che permette di calcolare tutte le frequenze che l'atomo di idrogeno eccitato può emettere tornando allo stato fondamentale (spettro di emissione) o assorbire eccitandosi (spettro di assorbimento), per ogni salto dell'elettrone fra due dei possibili stati stazionari di numeri quantici n₁ e n₂.

I principali limiti del modello di Bohr (già noti al tempo del modello) sono i seguenti:

(a) non funziona per atomi a più elettroni;

(b) non spiega i multipletti (righe osservate sperimentalmente molto vicine tra loro);

(c) non dà indicazioni sull’intensità delle righe.

Tutte cose che vedremo in seguito.

Prima di andare oltre e affrontare atomi più complicati, dove il modello di Bohr non riesce più a funzionare, vediamo dettagliatamente cosa succede esattamente al nostro semplice, ma fondamentale, idrogeno.

Basta disegnare un semplice diagramma, in cui sono rappresentate come linee orizzontali i vari livelli energetici delle orbite dell’elettrone. I balzi da una linea a un'altra causano differenze di energia e quindi differenti frequenze. Queste frequenze sono quelle relative alla righe dello spettro, come illustrato in Fig. 22.

 

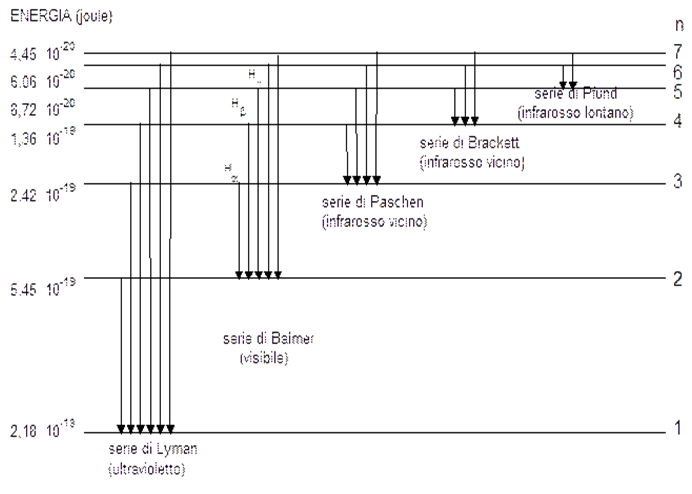
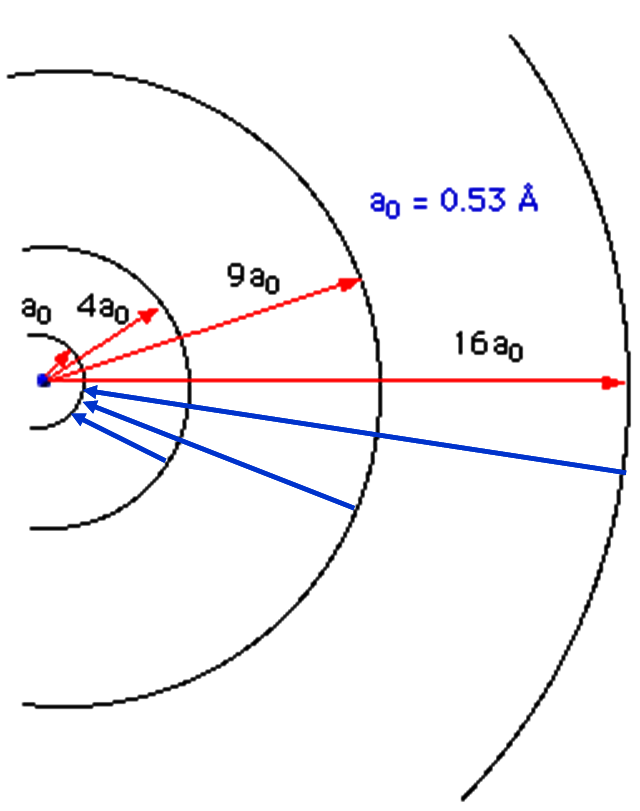
Volendo si può anche mostrare la situazione attraverso le vere e proprie orbite possibili degli elettroni (Fig. 23)

 

 

Righe chiare e righe scure

Se il salto assorbe energia (l’elettrone riceve energia) le righe appaiono scure nello spettro continuo. Perché? Perché l’atomo elimina dallo spettro di sfondo proprio l’energia relativa alle frequenze usate per far saltare gli elettroni. Quando poi l’elettrone torna al suo posto, l’energia è inviata in una direzione qualsiasi e non è assolutamente detto che arrivi all’osservatore (o quantomeno ne arriva solo una parte e quindi si abbassa l’intensità)

Se, invece, il salto è quello che riporta l’elettrone nelle condizioni originarie, si ha emissione di energia (righe luminose in assenza di spettro continuo). Si ha questa situazione, quando si eccita termicamente un gas rarefatto. La luce che si ottiene è solo quella emessa nei salti degli elettroni che tornano nel gradino di base. Non compare nessuno spettro continuo e si vedono solo le righe, relative ai salti che inviano la luce proprio verso l’osservatore.

Introduciamo la Fig. 24 per fare ancora maggiore chiarezza.

 

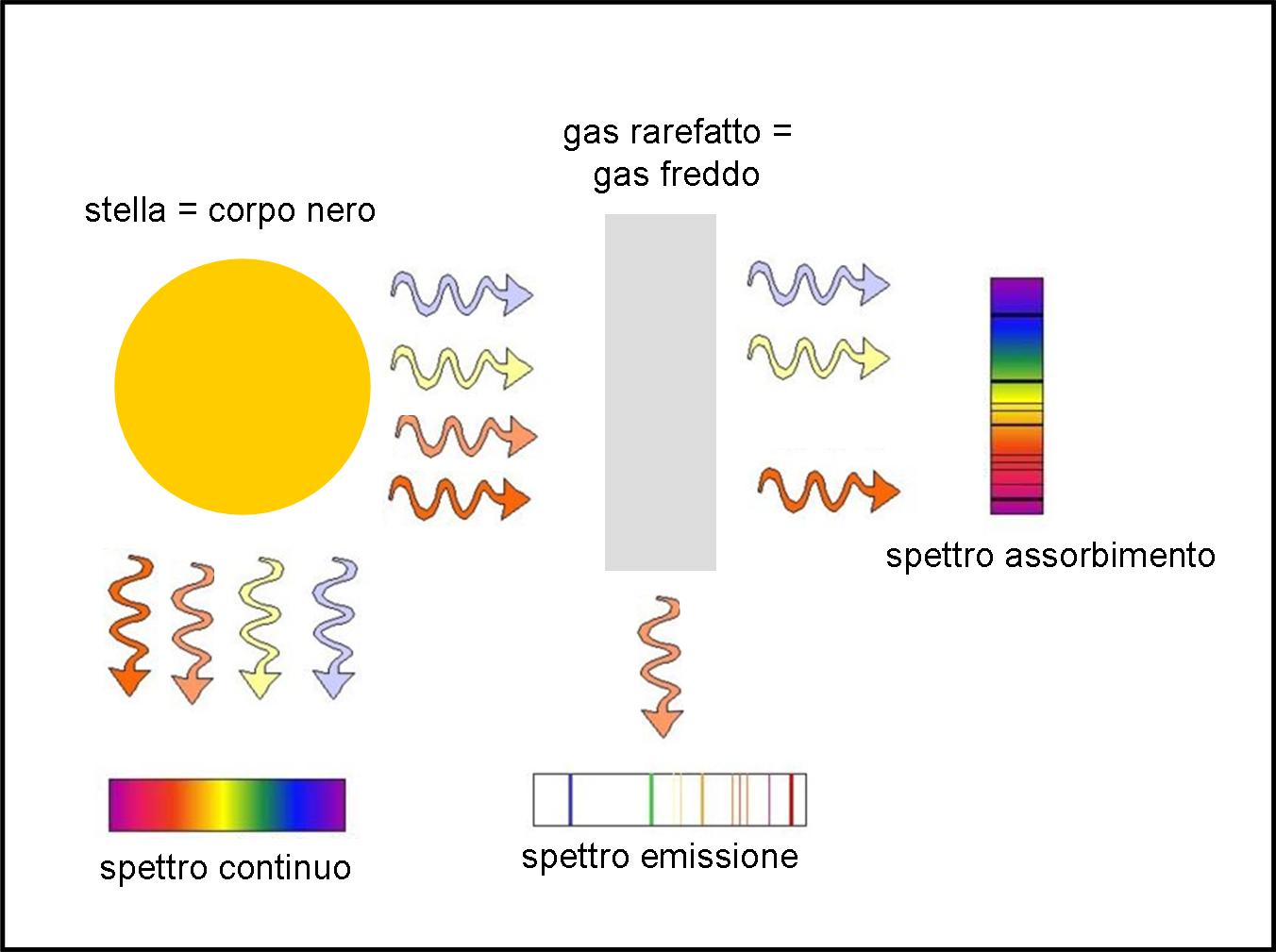
Una stella emette nel continuo come un corpo nero. Se assumiamo che essa sia esattamente un corpo nero riceviamo la luce in basso a sinistra. Se, invece, la luce della stella, prima di giungere a noi, deve attraversare del gas rarefatto e abbastanza freddo (atmosfera stellare, ad esempio), gli atomi di questo strato ricevono i fotoni della stella e quelli "giusti" fanno saltare gli elettroni solo da un livello a un altro (senza scacciarli del tutto). In altre parole, gli elettroni che saltano assorbono i fotoni di una certa lunghezza d'onda e non li fanno arrivare fino a noi (a destra in alto). E' vero che poi questi elettroni tornano a casa ed emettono fotoni, ma li possono mandare un po' ovunque e quelli che viaggiano proprio nella nostra direzione saranno ben pochi. In corrispondenza delle frequenze dei salti vediamo delle righe scure. Lo spettro è quello di assorbimento, in cui le righe si sovrappongono al continuo.

Se, però,  siamo sistemati a novanta gradi (in basso a destra) rispetto a una nube di gas rarefatto che viene investita dalla luce di una stella, cosa succede? Beh... di sicuro non vediamo lo spettro continuo della stella che attraversa la nube (bisognerebbe essere nella posizione di prima, in alto a destra). La nube, però, assorbe alcune frequenze e poi le rimette. Dato che le riemette in ogni direzione, qualche fotone riesce a raggiungere anche noi che siamo sistemati di lato. Ciò che vediamo sono, allora, solo le righe (luminose) che corrispondono ai fotoni emessi durante il salto degli elettroni. Abbiamo uno spettro di emissione.

Inseriamo anche la Fig. 25 per spiegare ancora meglio la differenza di come noi vediamo, a seconda della posizione, il lavoro fatto, nell'atomo del gas rarefatto investito dalla luce del continuo, dagli  elettroni "salterini". In pratica, tutto dipende dalla nostra posizione... In un caso, l'atomo riduce la luce di una certa frequenza, rispetto a quella libera di arrivare fino a noi. Nell'altro, quel poco che ci manda è l'unica cosa che riusciamo a vedere. Meglio poco che niente!

 

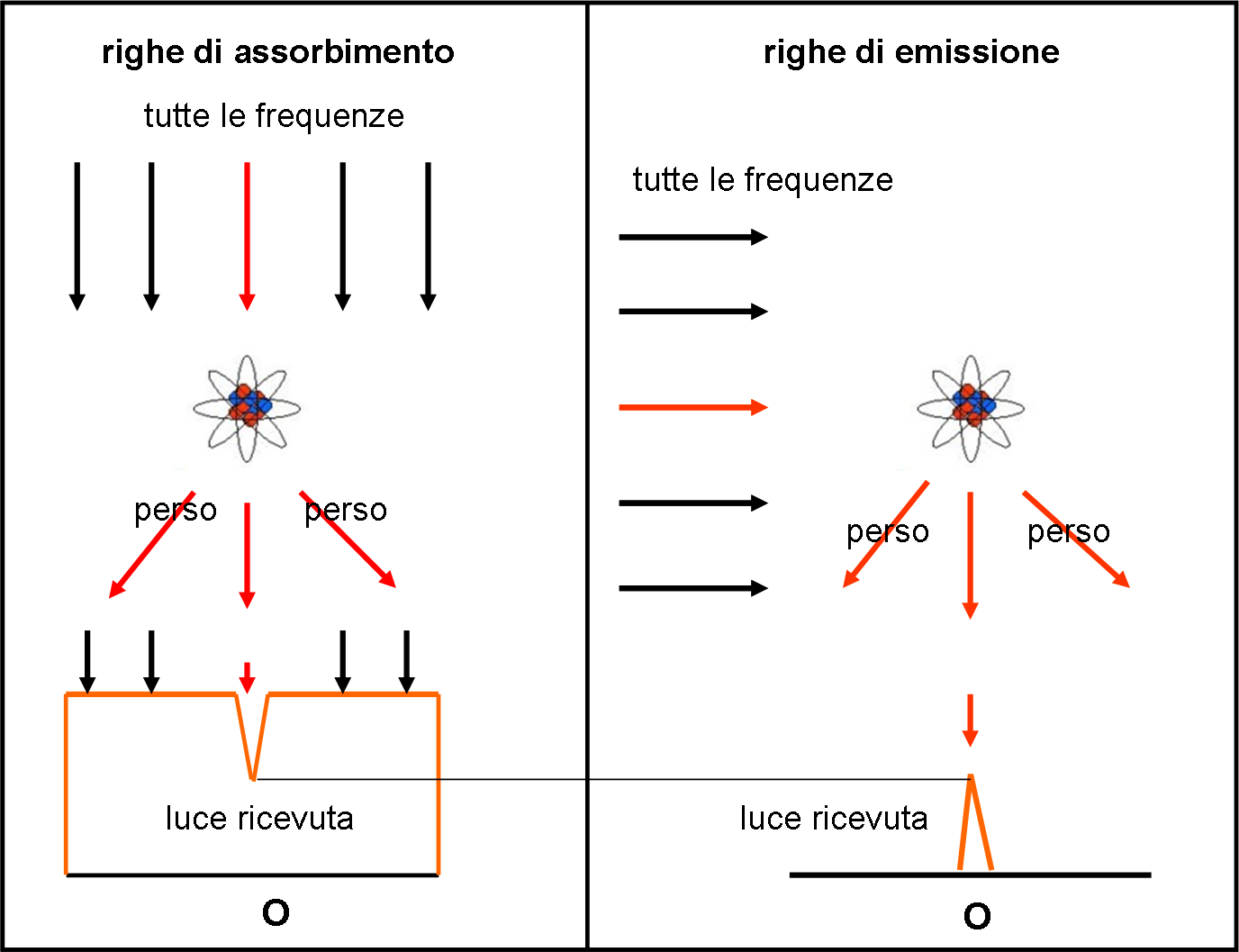
Le righe, proprio per come si ottengono, devono coincidere (uguale differenza di energia e quindi uguale frequenza).

Come e dove si sistemano queste righe? Le abbiamo già viste nella Fig. 22, ma è meglio ripetere ancora il concetto. Se l’elettrone inizia e termina il suo salto nell’orbita più bassa (più probabile e stabile, dato che ha la minima energia) abbiamo righe più energetiche (i salti sono più grandi). Se i salti avvengono tra righe più alte, le frequenze diventano sempre minori dato che le differenze di energia diminuiscono. Le righe si spostano, quindi, verso frequenze più basse (lunghezza d’onda maggiori).

I vari tipi di salti possibili e, quindi, di righe che “sporcano” lo spettro continuo si inseriscono in intervalli diversi di frequenze. Ricordiamo, infatti, che più i salti sono energetici e più le frequenze sono alte. Se l’orbita di partenza e di arrivo è quella più bassa di tutte troviamo righe che cadono nell’ultravioletto. Se è la seconda o la terza o la quarta, le righe si spostano verso lunghezze d’onda maggiori (frequenze minori). Ribadiamo ancora una volta, se ce ne fosse bisogno, che ad ogni orbita dell’elettrone corrisponde un certo numero di frequenze, dipendenti dall’orbita più alta raggiunta nel salto e dal livello raggiunto nel ritorno. Abbiamo così gruppi di righe relative a livelli finali diversi, i cui nomi sono riportati in Fig. 22. Ogni gruppo si sposta verso lunghezze d’onda più grandi.

Riassumendo: chi comanda la frequenza è soprattutto l'orbita stabile raggiunta alla fine, ma per ognuna di queste orbite finali vi sono varie righe che dipendono dall'orbita di partenza. Ad esempio, la righe di Lyman sono le più energetiche e cadono nell'ultravioletto, dato che l'orbita stabile finale è quella più bassa. Tuttavia, esse sono più di una, dato che l'energia dipende dall'orbita di partenza. Cambiando, poi, orbita finale,  ci si sposta verso lunghezze d'onda maggiori (l'energia finale è comunque minore), ma di nuovo ci saranno più righe a causa delle diverse orbite di partenza.

Da quanto abbiamo visto nelle figure precedenti, se del gas di idrogeno si trova negli strati più esterni e più freddi di una stella, lo spettro deve presentare le righe relative al suo atomo (righe di assorbimento). Se, invece, il gas è illuminato “di fianco” (nebulosa ad emissione) vediamo solo le righe di emissione dell’idrogeno. Le righe, comunque, mantengono sempre la stessa posizione, ossia hanno sempre la stessa frequenza.

Non è difficile capire che la presenza di certe righe ben definite ci dice che è presente l’idrogeno.

Come volevasi dimostrare: le righe sono proprio la carta d’identità di un certo elemento. Senza parlare, poi, della loro intensità e di tante altre caratteristiche che migliorano sempre più l’informazione. Mamma mia, quante informazioni in quel simpatico fotone, un pacchetto veramente insostituibile!

 

Perché solo orbite circolari?

Niente da dire. L’atomo di Bohr è sicuramente rivoluzionario come concetto e fa uso delle recentissime scoperte sull’energia “impacchettata”. Tuttavia, come già accennato, rimane ancora legato alla meccanica classica. Infatti, gli elettroni sono particelle ben definite che non possono trovarsi ovunque ma solo su certe orbite e che, quindi, possono permettersi salti più o meno energetici tra un gradino e l’altro (orbite), ma devono rapidamente tornare indietro. Nel frattempo, però,  la meccanica quantistica va rapidamente avanti con le sue regole sempre meno comprensibili e gli  atomi degli elementi più pesanti presentano righe spettrali che non possono essere spiegate con il semplice modello di Bohr. In fondo, esso fa sì uso dei pacchetti d’energia, ma simula  ancora perfettamente un sistema planetario, dove non tutte le orbite sono possibili, ma solo alcune. Più o meno quello che capita con i pianeti del Sistema Solare.

I pianeti, però, hanno orbite che non sono circolari... Si può ancora migliorare qualcosa.

Il primo passo verso qualcosa di più complicato lo propone Sommerfeld nel 1915, assumendo orbite ellittiche per gli elettroni. Un passo ancora disperato per non staccarsi dalle leggi di Keplero.

Infatti, il modello di Bohr riesce a spiegare abbastanza bene lo spettro di emissione dell'idrogeno e di qualche metallo alcalino come il sodio e il litio; per l'elio, però, già si osservavano delle righe formate da "multipletti", ovvero righe secondarie molto vicine tra loro. I salti quantici di Bohr non possono spiegarle. La differenza di frequenza tra le righe secondarie è molto piccola per cui è possibile che, ad esempio, tra lo stato fondamentale e lo stato eccitato n = 2 siano possibili diverse situazioni stabili secondarie, rilevabili dalle righe secondarie dello spettro.

Sommerfeld propone, allora, una teoria in cui si ipotizzano orbite ellittiche, che abbiano il semiasse uguale al raggio di Bohr. Anche questo sistema è quantizzato, per cui Sommerfeld definisce un secondo numero quantico, il numero quantico orbitale ( l ) che determina la "quantizzazione dell'eccentricità dell'ellisse" che l'elettrone può percorrere nei suoi stati stazionari. In altre parole, il numero quantico orbitale definisce la forma dell'orbita. La descrizione non è banalissima.

Nel primo livello, l'elettrone può percorrere solo un'orbita circolare e niente cambia rispetto all'atomo di Bohr. Nel secondo livello oltre all'orbita circolare, l'elettrone può anche percorrere un'orbita ellittica. Nel terzo livello  l'elettrone può occupare, oltre all'orbita circolare, due orbite ellittiche aventi sempre assi maggiori uguali al diametro dell'orbita circolare, ma con diversa eccentricità e cosi via. In altre parole, ad ogni livello n stabilito dal numero quantico principale, si associano n-1 orbite ellittiche. Qualcosa come quella rappresentata nella Fig. 26.

 

 

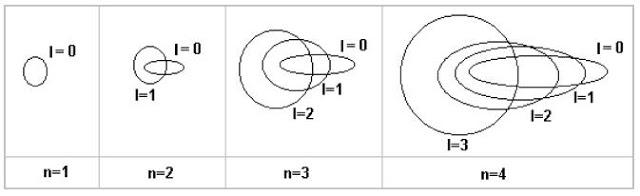
L'introduzione delle orbite ellittiche sembra rappresentare un' inutile complicazione nei calcoli. E, invece, riescono a spiegare  la struttura fine delle righe spettrali. Sembrerebbe impossibile, dato che, in fondo, le orbite dovrebbero avere la stessa energia...

Bisogna  tenere conto che la teoria di Bohr è una teoria non relativistica, nel senso che non utilizza  le relazioni della relatività speciale. Esse possono essere trascurate solo se i corpi che si stanno studiando hanno velocità molto inferiori alla velocità della luce.  L'elettrone è, però, proprio un qualcosa che ruota a velocità molto elevate e la relatività non può essere messa sotto al tappeto.

In pratica,  nel moto lungo un'ellisse, l'elettrone è costretto a viaggiare più velocemente quando si trova più vicino al nucleo e più lentamente quando si trova più distante. La massa stessa subisce delle modificazioni, aumentando in prossimità del nucleo e diminuendo nel punto più distante. Ciò comporta una  minima diversità delle energie associate alle orbite ellittiche, le quali non coincidono più con le energie delle orbite circolari dello stesso livello di Bohr.

Sommerfeld, insieme alla teoria della relatività, ha risolto, in parte, il problema!

 

Keplero non abita più qui...

Però, ormai, questo tipo di modello “kepleriano” si scontra sempre più con la meccanica quantistica e con i suoi principi, primo fra tutti quello di esclusione di Pauli. Al posto delle orbite subentrano gli orbitali, legati alla probabilità di un elettrone di stare in una certa regione attorno al nucleo. I numeri quantici si moltiplicano e piano piano si crea un'elegante e pressoché perfetta corrispondenza degli orbitali atomici con la Tavola Periodica degli elementi.

Anche se la spettroscopia sempre più fine non può evitare di risentire di queste continue migliorie, la faccenda si complica sempre di più.  La struttura dell'atomo e tutti i suoi simpatici numeri quantici li vedremo  in seguito.

Fermiamoci a questo livello e... usciamo a rivedere le stelle (e i loro spettri)!

 

La serie completa "Dall'Atomo alle stelle e viceversa" è disponibile QUI