Un classico paradosso che, per molti, non è ancora stato risolto. Ma è veramente un paradosso o solo una specie di fake news?

Questo articolo è legato al calcolo delle probabilità e riporta un vero e proprio paradosso ideato dal matematico francese Bertrand. Un paradosso che da molti è considerato ancora insoluto e che altri si sono limitati a risolvere in modo rozzamente semplificato. Sul web troverete di tutto e di più. Io ho trovato estremamente interessante la descrizione data in questo libro e ad esso mi rifaccio. Un’analisi dettagliata mostra come faccia nascere grossi problemi in una parte fondamentale della matematica, come è la probabilità, con le sue ovvie ricadute sulla meccanica quantistica, che di una corretta definizione di probabilità ha grande necessità.

Un argomento che tocca gli insiemi, numerabili e no, che il nostro collaboratore Umberto avrebbe saputo descrivere con maggiore precisione e rigore matematico. Io ho cercato di semplificare al massimo, sperando di far comprendere, magari in modo un po’ empirico, il concetto di fondo. Lo dedico a Umberto, sperando di non farlo arrabbiare troppo …

 

Il paradosso di Bertrand 

Joseph Bertrand è stato un matematico francese che nel 1889 pose una semplice domanda concernente il problema della probabilità di una certa azione. Ma, oltre  a porre la domanda diede anche tre risposte che appaiono ancora oggi (anche se non per tutti) perfettamente corrette nel loro sviluppo. L'enunciato sembra veramente banale, ma proprio in esso si può evidenziare già l'ambiguità delle risposte.

Andiamo avanti con molta lentezza e cautela, cercando di mostrare come il problema sia in effetti composto da una parte decisamente semplice, ma anche da una parte molto più complessa e sottile che ci porta direttamente ai principi della meccanica quantistica.

Dato un triangolo equilatero inscritto in una circonferenza e una corda del cerchio scelta casualmente, il problema consiste nel determinare la probabilità che la corda sia più lunga de lato l del triangolo.

Bertrand si diverte a proporre tre soluzioni completamente diverse tra loro, ma che apparentemente sono tutte statisticamente corrette.

1)    Metodo dell’angolo o dei due estremi casuali

Consideriamo un punto Q qualsiasi della circonferenza e tracciamo la tangente in quel punto. Prendiamo una retta qualsiasi che passi per quel punto e facciamola ruotare in modo che intersechi la circonferenza in un altro punto Q’.  Ovviamente, come mostra la Fig. 1, l’angolo che questa retta fa con la tangente, per ottenere il risultato voluto, va da 0° a 180°.

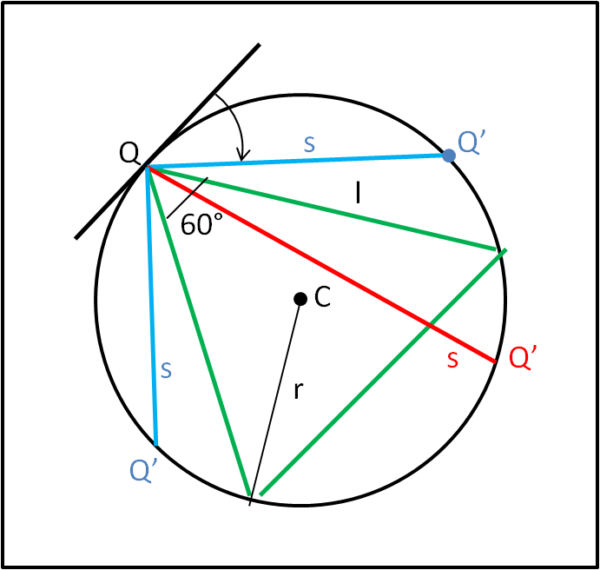
Prendiamo, ora, il triangolo equilatero che ha un vertice nel punto Q. Una semplicissima analisi delle possibilità che derivano da questo approccio ci dice che, affinché la corda, ottenuta durante la rotazione della retta, risulti maggiore del lato l del triangolo, essa deve essere interna al triangolo, ossia l’angolo che forma con la tangente deve essere maggiore di 60° e minore di 120°, dato che l’angolo di un triangolo equilatero è sicuramente uguale a 60°. Ne segue che, per qualsiasi punto Q scelto sulla circonferenza, le corde che ne derivano rispondono al requisito della formulazione di Bertrand se e solo se l’angolo rispetto alla tangente cade nell’intervallo tra 60° e 120°. Questo intervallo vale 60° e, quindi, la probabilità che la corda scelta a caso sia maggiore del lato del triangolo è data da:

P(s > l) = 60/180 = 1/3

Riassumendo: l’angolo può variare nell’intervallo 0-180°, ma le corde maggiori del lato l si hanno solo per un angolo ristretto, pari a 1/3 dell’angolo piatto.

Tutto sembra perfetto, dato che il punto Q è stato scelto a caso assumendo una distribuzione uniforme dei punti sulla circonferenza.

Tutto bene? Nemmeno per sogno!

Cambiamo approccio per ottenere la probabilità richiesta da Bertrand

2)  Metodo della distanza o del raggio casuale

Disegniamo, in Fig. 2, un raggio r qualsiasi della circonferenza.

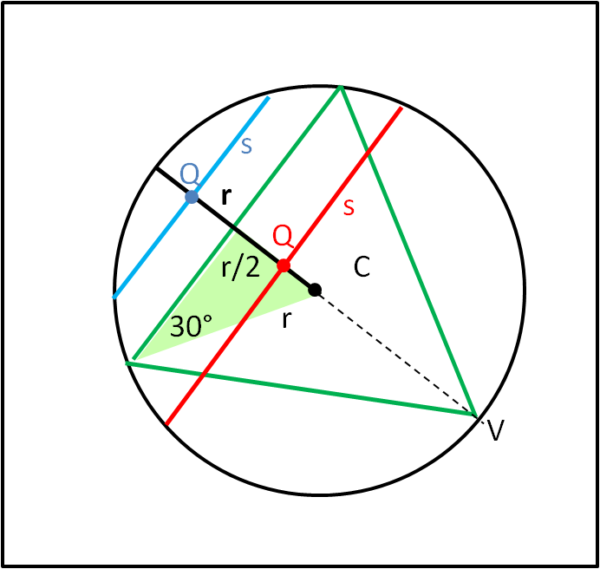
Prolunghiamolo fino a che incontri la circonferenza in V, dove poniamo un vertice del triangolo equilatero. Sul raggio r scegliamo a caso un punto Q e tracciamo la perpendicolare al raggio. Essa determina sicuramente una corda che, per come è stata ottenuta, è scelta del tutto casualmente come il vertice del triangolo. La distribuzione dei punti lungo il raggio è, ovviamente, uniforme. Risulta subito chiaro che questa corda è maggiore del lato l del triangolo solo e soltanto se la distanza tra il centro C e il punto Q è minore di r/2 (Fig. 3). In conclusione la probabilità di avere una corda maggiore del lato è data dal rapporto tra 1/2 r e r, ossia:

P(s > l) =  1/2 r/ r = 1/2

Accidenti! Un valore del tutto diverso da quello ottenuto prima, ma che sembra avere seguito le regole della scelta casuale della corda, avendo scelto casualmente la distanza lungo il raggio della circonferenza. Oltretutto anche il raggio è stato scelto casualmente. In poche parole, dato il raggio esiste una e una sola corda che sia ad esso perpendicolare e che abbia una certa distanza dal centro. La distribuzione dei raggi è uniforme e tale sarà anche quella della corda corrispondente.

La situazione è sicuramente critica, ma Bertrand vuole esagerare e introduce un terzo approccio…

3)   Metodo della posizione o del punto medio

In Fig. 3, consideriamo un punto Q qualsiasi all’interno del nostro cerchio e tracciamo la corda che abbia questo punto come punto medio.

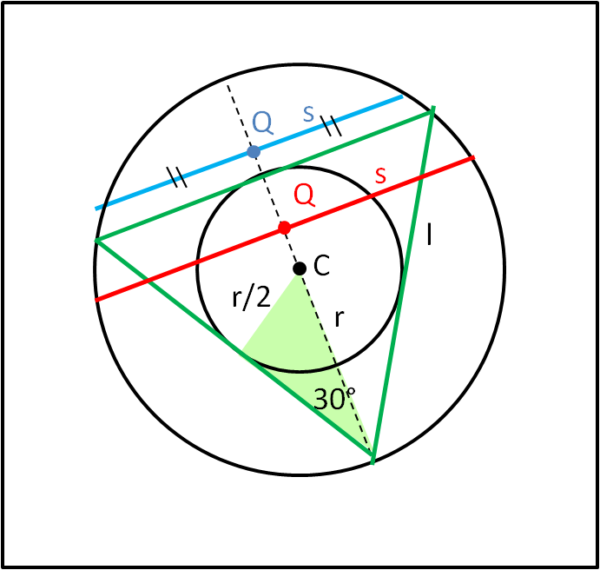
Consideriamo il cerchio inscritto al triangolo equilatero, sapendo che il suo raggio è la metà di quello di partenza. E’ immediato notare che esiste una e una sola corda che abbia Q come punto medio e quindi la scelta casuale di Q implica una scelta casuale della corda.  Questa corda, però, è maggiore del lato del triangolo se e solo se il punto Q è interno al cerchio inscritto nel triangolo. Qual è la probabilità che il punto Q sia interno al cerchio più piccolo, ossia che la corda sia maggiore del lato l? Beh… i punti sono distribuiti a caso e quindi la probabilità è data dall’area del cerchio inscritto divisa per l’area del cerchio di partenza:

P(s > l) = (π r²/4)/ (π r²) = 1/4

Un nuovo approccio e un nuovo risultato.

C’è sicuramente qualcosa che non va in tutta la faccenda. Eppure i metodi proposti sono tutti e tre perfettamente validi secondo le leggi della probabilità. Ribadiamo che nel primo caso il punto è scelto a caso sulla circonferenza, nel secondo è scelto a caso su un raggio e nel terzo è scelto a caso all'interno del cerchio. La cosa migliore da fare è allora quella di tornare all’enunciato di Bertrand e vedere se è l'enunciato stesso ad avere già un problema di base. Per fare questo cercheremo  un esempio pratico e ci faremo aiutare dal “solito” giocatore di golf. Alla prossima...

Continua…