Questo articolo è inserito in Matematica e Geometria

 

Concludiamo la dimostrazione della formula di Brahmagupta (QUI la prima parte), con molta pazienza e attenzione...

Continuiamo la nostra dimostrazione ricordando una proprietà dei quadrilateri ciclici: la somma degli angoli interni opposti è uguale a 180°.

(E) Vediamo allora la Fig. 7

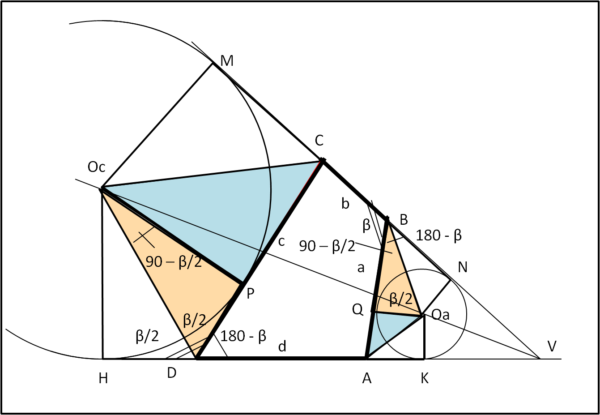
Chiamiamo β l'angolo CBA. L'angolo CDA vale allora 180 - β. Ma 180 - β è anche l'ampiezza dell'angolo QBN. Per costruzione, però, QBOa è la metà di QBN e, quindi vale (180 - β)/2 = 90 - β/2. L'angolo HDP deve valere β e, di conseguenza, OcDP vale β/2. In conclusione, i due triangoli rosa sono rettangoli e hanno gli altri due angoli congruenti. Ne segue che sono simili. In modo analogo, sono simili tra loro anche i triangoli azzurri.

Quanto trovato si estende anche agli altri triangoli rosa e azzurri di Fig. 8

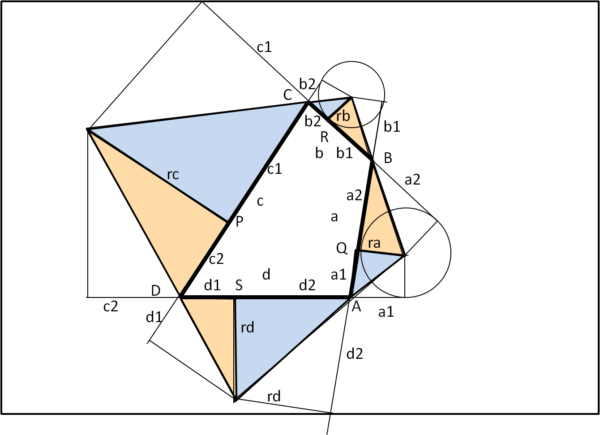
Non spaventatevi di tutte le lettere che sono state inserite. In particolare, i lati del quadrilatero di partenza sono stati divisi in due segmenti (a1, a2, b1, b2, c1, c2 e d1,d2). Con questa notazione, possiamo scrivere i rapporti tra lati dei triangoli simili rosa:

ra/a2 = rb/b1 = c2/rc = d1/rd

e dei triangoli azzurri:

rb/b2 = rc/c1 = d2/rd = a1/ra

Dai rapporti "rosa" possiamo facilmente scrivere:

ra rc = a2 c2

ra rd = a2 d1

rb rc = b1 c2

rb rd = b1 d1

mentre da quelli "azzurri", si ha

rb rd = b2 d2

rc rd = c1 d2

ra rb = a1 b2

ra rc = a1 c1

(F) Teniamoceli ben stretti e torniamo alla nostra area K del quadrilatero. Avevamo trovato, dalla (2) e dalla (3), che:

K = ra sa + rc sc           .... (2)

K = rb sb + rd sd         ....(3)

Ricordiamo inoltre che ciò che dobbiamo dimostrare è

K = √(sa sb sc sd)                    .... (4)

dove (ricordiamo...)

sa = s - a

sb = s - b

sc = s - c

sd = s - d

Quadrando la (4)

K² = sa sb sc sd                 .... (5)

Ci basta, perciò, dimostrare la (5).

Dalla (2) e dalla (3) abbiamo due modi per scrivere K e, quindi, moltiplicando tra loro i secondi membri otteniamo il valore di K² 

K² = (ra sa + rc sc)(rb sb + rd sd) = ra rb sa sb + ra rd sa sd + rb rc sb sc + rc rd sc sd   

Bellissima espressione anche se compaiono i prodotti dei raggi. Ma questo non è un problema ricordando le relazioni che avevamo messo da parte in (E), ossia:

ra rc = a2 c2

ra rd = a2 d1

rb rc = b1 c2

rb rd = b1 d1

rb rd = b2 d2

rc rd = c1 d2

ra rb = a1 b2

ra rc = a1 c1

Utilizzando queste uguaglianze, possiamo sostituire i prodotti dei raggi con dei prodotti tra "parti" dei lati ed è già un passo in avanti. In particolare, utilizziamo le relazioni in neretto

K² = (ra sa + rc sc)(rb sb + rd sd) = a1 b2 sa sb + a2 d1 sa sd + b1 c2 sb sc + c1 d2 sc sd   

Ancora una volta dobbiamo tornare indietro e ricordare quanto valeva il semiperimetro s. Abbiamo quattro modi per scriverlo:

s = c1 + b + a2

s = b2 + c + d1

s = c2 + d + a1

s = d2 + a + b1

ossia:

(s - b) = sb = a2 + c1

(s - c) = sc = b2 + d1

(s - d) = sd = a1 + c2

(s - a) = sa = b1 + d2

Consideriamo i termini non in neretto

ra rc = a2 c2

ra rc =  a1 c1

rb rd = b1 d1

rb rd = b2 d2

dalle prime due abbiamo:

a1 c1 = a2 c2 

da cui due relazioni

a2/a1 = c1/c2

a1/a2 = c2/c1

Consideriamo la prima e aggiungiamo 1 da entrambi i lati

a2/a1 + 1 = c1/c2 + 1

(a2 + a1)/a1 = (c1 + c2)/c2

a/a1 = c/c2

c2/a1 = c/a                                         .... (7)

abbiamo due possibilità:

 (c2 + a1): a1 = (c + a): a                      ....(*)

 (c2 + a1): c2 = (c + a): c                     ....(**)

sostituendo c2 + a1 = sd

Dalla (*) otteniamo:

sd/a1 = (a + c)/a

a1 (a + c) = sd a

a1 = sd (a/(a + c))            .... (8)

Dalla (**) otteniamo:

sd/c2 = (a + c)/c

c2 = sd (c/(a + c))            .... (9)

Consideriamo, adesso, la seconda uguaglianza, ossia:

a1/a2 = c2/c1

aggiungiamo 1 a entrambi i membri

a1/a2 + 1 = c2/c1 + 1

(a2 + a1)/a2 = (c1 + c2)/c1

a/a2 = c/c1

c1/a2 = c/a

abbiamo di nuovo due possibilità:

(c1 + a2): a2 = (c + a): a              ....(*)

(c1 + a2): c1 = (c + a): c              ....(**)

sostituendo c1 + a2 = sb

Dalla (*) otteniamo:

sb/a2 = (a + c)/a

a2 (a + c) = sb a

a2 = sb (a/(a + c))                   .... (10)

Dalla (**) otteniamo:

sb/c1 = (a + c)/c

c1 = sb (c/(a + c))                    .... (11)

Analogo procedimento si segue per le altre due uguaglianze

rb rd = b1 d1

rb rd = b2 d2

che portano a

b1 d1 = b2 d2

Siamo nelle stesse condizioni di (7) e svolgiamo i calcoli nello stesso modo, ottenendo:

b1 = sa(b/(b + d))               .... (12)

b2 = sc(b/(b + d))               .... (13)

d1 = sc(d/(b + d))               .... (14)

d2 = sa(d/(b + d))              .... (15)

Riassumiamo le relazioni da (8) a (15) che ci forniscono i valori di a1, b1, a2, b2, c1, c2, d1, d2.

a1 = sd (a/(a + c)) 

a2 = sb (a/(a + c))

b1 = sa(b/(b + d))

b2 = sc(b/(b + d)) 

c1 = sb (c/(a + c)) 

c2 = sd (c/(a + c))

d1 = sc(d/(b + d))

d2 = sa(d/(b + d))  

(G) Siamo quasi alla fine... dato che ci basta sostituire a1, ....., d2 con i valori appena trovati

K²= a1 b2 sa sb + a2 d1 sa sd + b1 c2 sb sc + c1 d2 sc sd

Prima di scrivere il prossimo passaggio notiamo che a1 b2 porta alla  moltiplicazione per  sd sc, il che vuol dire avere la quantità sa sb sc sd. Analoga situazione per gli altri quattro prodotti del secondo membro. Possiamo perciò mettere in evidenza sa sb sc sd:

K2 = sa sb sc sd [(a/(a +c)) (b/(b + d)) + ((a/(a + c) (d/(b + d)) + ((b/(b + d) (c/(a + c)) + (c/(a + c) (d/(b + d))]

Lavoriamo soltanto sulla parentesi quadra e raccogliamo dai primi due prodotti a/(a + c) e dai secondi due c/(a + c)

(a/(a +c)) ((b/(b + d)) + (d/(b + d))) + c/(a + c) ((b /(b + d) + (d/(b + d)))

Ma

b/(b + d) + d/(b + d) =( b + d)/(b + d) = 1

Non ci rimane che

a/(a +c) + c/(a + c)

ma anch'essa fa poca strada

a/(a +c) + c/(a + c) = (a + c)/( a + c) = 1

Ne consegue che

K² = sa sb sc sd

e, quindi:

K = √(sa sb sc sd)

proprio quello che volevamo dimostrare !

Sicuramente B. avrà usato un altro metodo, ma noi siamo abbastanza contenti di avere utilizzato solo e soltanto passaggi geometrici e un minimo di calcolo elementare. L'impresa è stata lunga e abbastanza difficile, ma il risultato dona una grande soddisfazione non avendo usato né trigonometria e nemmeno la formula di Erone. Quest'ultima, ovviamente, si ottiene ponendo d = 0, ossia riducendosi a un triangolo ( sd = (s - d) = s).