Categorie: Matematica
Tags: area cubo geometria ombra proiezione ortogonale quiz
Scritto da: Vincenzo Zappalà
Commenti:14
(QI) Giochiamo con l'ombra **/****
Dobbiamo ammettere che ha fatto (e sta ancora facendo in varie regioni) un gran caldo. Il Sole picchia senza pietà e si cerca in tutti i modi di trovare un po' d'ombra. Immaginiamo di avere il Sole allo zenit (anche se da noi è impossibile) e di utilizzare una bella tenda quadrata. Bene, se la mettiamo perpendicolare ai raggi solari, abbiamo una bella ombra quadrata che, ovviamente, si trasforma in un rettangolo se incliniamo la tenda o se il Sole comincia ad abbassarsi. La Fig. 1 mostra la situazione che è di una banalità incredibile.
Dato che siamo sempre pronti a complicare le cose, immaginiamo che la nostra "tenda" si trasformi in un cubo. Beh, se il cubo viene messo con la faccia inferiore parallela al pavimento, e il Sole è sempre allo zenit, l'ombra che ne risulta è identica a quella del quadrato. Però, però... le cose cambiano se incliniamo il cubo o, ancor peggio, se lo ruotiamo a piacere attorno al suo centro O (incrocio delle diagonali maggiori).
Ed eccoci alle nostre domande.
(1) Che forma ha l'area massima dell'ombra? **
(2) Ricavare la formula che ci dona, per qualsiasi configurazione, l'area dell'ombra del cubo proiettata sul pavimento ****
Per risolvere i due problemi, bisogna fare uso della trigonometria e saper visualizzare bene una figura a tre dimensioni. Io ho adottato un metodo, ma può darsi che ne esistano altri, magari più facili ed eleganti...
Forza miei prodi, l'ombra vi aspetta!
QUI la soluzione
14 commenti
Sono riuscito solo a ricavare l'area dell'ombra se il cubo (di lato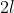
) ruota attorno all'asse x o y, ma non a combinare le due rotazioni.
In caso di rotazione 'pura' di un angolo
attorno ad un asse l'ombra ha area )
, con ovvio massimo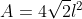 
per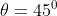 
.
Qui sotto un'orrenda immagine per dimostrare quanto sopra. Anche se non sembra OA=OB=l (semilato), quindi l'ascissa di B è=l\sqrt{2}(sin\theta&space;cos45+cos\theta&space;sin45)=l(sin\theta&space;+cos\theta&space;))
Rotazioni attorno all'asse z non modificano né forma né dimensioni.
In attesa della risposta completa continuo a pensarci.
Errorino: va letto " Anche se non sembra OA=AB=l"
Caro Enzo,
intanto inizio con il calcolare la diagonale che unisce due vertici opposti di due facce opposte:
se, per semplicità, si fissa il lato del cubo come unitario, la diagonale che unisce due vertici opposti della stessa faccia è
e va a formare un triangolo rettangolo i cui cateti misurano 1 (il lato del cubo) e 
allora, applicando il teorema di Pitagora, la diagonale ricercata (ipotenusa del nostro triangolo rettangolo) sarà
Se pongo il cubo con tale diagonale perpendicolare al piano di terra, la sua proiezione, con i raggi luminosi perpendicolari al piano di terra (ovvero paralleli alla diagonale maggiore), dovrebbe disegnare un bell'esagono regolare.
Ora, se faccio una sezione trasversale del cubo posto come in precedenza e focalizzo il triangolo rettangolo di cui sopra, dovrei ottenere una figura del genere:
la linea rossa è la proiezione del lato del cubo sul piano di terra, che rappresenta il segmento che unisce uno dei vertici dell'esagono ombra con il centro dell'esagono stesso (cioè quello che si vede guardando dall'alto perpendicolarmente);
ma dato che un esagono regolare si può considerare coma la composizione di sei triangoli equilateri che condividono tutti uno stesso vertice, la linea rossa sarà uguale al lato dell'esagono ombra.
Ricavo la sua misura con la geometria euclidea (la linea rossa è l'altezza sull'ipotenusa di quel triangolo rettangolo) come cateto × cateto / ipotenusa, ovvero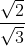
e siccome l'area di un esagono regolare è pari a:
sostituendo ad 
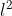il valore
Forse questa è l'area massima, così come, ad "intuito", variando l'angolazione dell'asse-diagonale, l'ombra dovrebbe disegnare esagoni più o meno "allungati", ma ripeto, è una mia sensazione.
Per adesso mi fermo qui.
Mamma mia! Mi è venuta fuori un'espressione terrificante per l'area dell'ombra in funzione di
e 
, angoli tra l'asse x ed y. La riporto, ma fa paura...
A parziale giustificazione di questa mostruosità osservo che se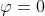
ottengo la formula di prima per una rotazione attorno all'asse x.
Naturalmente possono essere errate entrambe...
Eh già... mi sa che son proprio sbagliate! Vabbé, 4* per me son troppi :-)
Questo caldo afoso mi ha fatto sorgere alcune considerazioni;
provo a mettere il cubo coricato su di un lato aderente al terreno con la diagonale di una faccia perpendicolare al piano di terra:
provo a cambiare angolazione, sempre con le stesse condizioni di prima:
e quindi Area = 1 × (√3 / 2 + 1 /2).....e "qui casca l'asino", perché se considero il segmento perpendicolare al piano di terra che parte dal vertice più distante (dal piano di terra), la sua misura sarà √2 × sin(45° + 30°)
e usando le formule trigonometriche di addizione degli angoli:
sin(45° + 30°) = sin(45°)cos(30°) + sin(30°)cos(45°) = √2 / 4 + √6 / 4
quindi √2 × (√2 / 4 + √6 / 4) = 1 / 2 + √3 / 2, cioè il valore dell'area del rettangolo ombra poc'anzi trovato.
Ovviamente se il cubo e posto su una faccia, l'area dell'ombra sarà 1 × 1 = 1.
Ricapitolando, quando il punto sulla superficie del cubo più distante perpendicolarmente dal piano di terra (altezza) è:
√3 area dell'ombra → 1 × √3 = √3
√2 area dell'ombra → 1 × √2 = √2
(√3 / 2 + 1 /2) area dell'ombra → 1 × (√3 / 2 + 1 /2) = √3 / 2 + 1 /2
1 area dell'ombra → 1 × 1 = 1
Quattro indizi non fanno una prova, ma il sospetto è legittimo:
non è che l'area dell'ombra (con i raggi del sole sempre perpendicolari al piano di terra) è data dal prodotto del lato del cubo per l'altezza come prima definita?
fuochino, fuochino....
Caro Enzo,
Per cercare di risolvere il problema ho chiesto aiuto a:………….una sfera!
Nel senso che ho immaginato una sfera poggiata su un piano e un asse perpendicolare al piano e passante per il centro della sfera stessa che identifica due punti sulla sua superficie: un “polo sud” nel punto di contatto tra sfera e piano e un “polo nord” in posizione diametralmente opposta; ho considerato un secondo asse perpendicolare al primo (e parallelo al piano del foglio) e passante sempre per il centro della sfera che identifica nella stessa maniera di prima un “polo est” e un “polo ovest”.
Ora, posso portare “davanti al mio naso”, qualsiasi punto sulla sfera attraverso delle rotazioni su se stessi, singole o combinate, dell’asse nord-sud e dell’asse est-ovest.
Questa lunga premessa mi ha portato a considerare allora se fosse opportuno ricorrere al sistema di coordinate polari sferiche per la risoluzione del problema, operando delle “forzature” che possono compromettere formalmente e sostanzialmente la correttezza dei risultati.
Considero il cubo in un riferimento tridimensionale:
e chiamo α l'angolo di rotazione su se stesso dell’asse x e β l’angolo di rotazione su se stesso dell’asse z ed r la distanza dall’origine degli assi che pongo pari al lato del cubo (prima forzatura).
Se pongo d la distanza massima di un punto sulla superficie del cubo con il piano di terra, sommando le sue tre coordinate polari espresse in un sistema cartesiano (seconda forzatura):
Il cubo "a riposo" cioè con una faccia poggiata sul terreno, ruotando solo l'asse x di 45° ,
cioè α = 45 e β = 0 con uno spigolo poggiato sul terreno farà si che la distanza massima da terra sia:
d = r sin(45) cos(0) + r sin(45) sin(0) + r cos(45) = r (√2 / 2 + 0 + √2 / 2) = r √2
area dell'ombra r × r √2
Con una rotazione di 60°, α = 60 e β = 0, con lo stesso spigolo poggiato sul terreno:
d = r sin(60) cos(0) + r sin(60) sin(0) + r cos(60) = r (√3 / 2 + 0 + 1 / 2 ) = r (√3 / 2 + 1 / 2 )
area dell'ombra r × r (√3 / 2 + 1 / 2 )
Stando fermo sulla posizione di riposo, α = β = 0
d = r sin(0) cos(0) + r sin(0) sin(0) + r cos(0) = r
area dell'ombra r × r.
Ripeto, è un tentativo "fantasioso" e probabilmente errato, per supportare il mio "più che sospetto" che l'area dell'ombra sia il lato del cubo per l'altezza massima di un suo punto dalla superficie...
bravo Andy,
tuttavia mi sembra che manchi ancora la formula che descrive l'area dell'ombra nel caso più generale possibile o sbaglio?
Caro Enzo,
perdona la mia testa dura, ma se la tua domanda si riferisce ad una forma generica di area A che proietta la sua ombra sul terreno (con i raggi luminosi sempre perpendicolari), questa dovrebbe essere:
Area_ombra = A × cos(θ) dove θ è l'angolo formato dal piano dove giace la figura con il piano di terra;
faccio un esempio pratico:
un rettangolo, inizialmente parallelo al piano di terra, ruotato di 60° secondo l'asse passante per il lato lungo, proietta un ombra rettangolare dove la proiezione del lato corto sul piano di terra è
lato corto × cos(60°) = lato corto × 1 / 2, quindi l'area dell'ombra sarà
lato lungo × (lato corto × 1 / 2) = metà area del rettangolo
Probabilmente il discorso dovrebbe valere anche per aree di forma irregolare, l'importante che ruotino secondo un asse costantemente parallelo al piano di terra.
Tornando un attimo al nostro cubo, ho notato che così come sono disposti gli assi che ho disegnato, i movimenti rotatori dell'asse x e z devono avvenire in senso orario, perché se la posizione inziale del cubo è con una faccia poggiata sul terreno, la rotazione antioraria degli assi lo "interrerebbe", (per avere una rotazione antioraria, basta scambiare l'asse x con l'asse y) ma in ogni caso l'angolo spazzato è sempre lo stesso.
Un'ultima considerazione: se l'asse x viene ruotato di un angolo pari all'angolo maggiore complementare del triangolo rettangolo 1, √2, √3,
quindi
= )
= )
= )
= 54°,73561....
(in gradi sessagesimali 54° 44' 8.2'') e successivamente l'asse z viene ruotato di 45°, quindi
= 45°,
il cubo si dispone con la diagonale maggiore (quella che misura √3) perpendicolare al piano di terra,
proietta un esagono regolare di area:
r × r ( sin(54°,73561) cos (45°) + sin(54°,73561) sin(45°) + cos(54°,73561) = r × r × √3
che il valore massimò dell'ombra trovata precedentemente senza l'uso della trigonometria.
Adesso stacco un po' perché la testa mi è diventata un.............cubo!
caro Andy,
sono perfettamente d'accordo con te sulla proiezione di una figura piana. Il cubo, però, non s'interra perché non è poggiato sul piano x,y ma posto, all'inizio, con una faccia PARALLELA al paino (x,y), per cui può girare a piacimento. Sono anche d'accordo sull'area massima, ma la formula generica dell'area proiettata pu0 essere calcolata con una sola formula generale e non valida solo nei casi particolari. Penso che tu abbia già compreso quella formula, ma io la vorrei determinata per qualsiasi posizione del cubo (sempre che ne basti una e una sola) e non ricavata in base a risultati di posizioni particolari. Ma forse non ci capiamo...
Caro Enzo,
probabilmente diciamo la stessa cosa in termini differenti.
Cercherò di essere più chiaro: ai fini "proiettivi" non cambia nulla se anziché poggiato sul terreno, immaginiamo 2 piani paralleli tra loro e paralleli al piano di terra:
i 2 piani paralleli potrebbero essere, per fare un esempio immediatamente viso, i palmi di due mani che contengono perfettamente il nostro cubo.
La distanza tra questi 2 piani paralleli rappresenta quella che ho chiamato altezza del cubo dal piano di terra (nel caso del cubo direttamente a contatto con il terreno);
se il cubo e poggiato su una faccia sul palmo inferiore, la distanza tra i due palmi (che chiamavo altezza del cubo) sarà il lato del cubo,
se il cubo ha un punto di contatto sul palmo inferiore ed uno sul palmo superiore secondo la sua diagonale più lunga disposta perpendicolarmente ai due palmi, la distanza alias altezza è √3 e così via.
Ora, ruotando il cubo in relazione a 2 assi perpendicolari x e z, di un sistema tridimensionale xyz i cui piani xy, xz e yz sono perpendicolari tra loro, queste rotazioni variano la distanza tra i due piani contenenti perfettamente il cubo (ovvero cambiano le coordinate spaziali di un punto dall'origine degli assi nel sistema di riferimento xyz);
siccome tale distanza dipende dalla variazione di due angoli (riferiti a due assi), si può scrivere
h = l × f(α, β) dove l è il lato del cubo e f(α, β) = sin(α)cos(β) + sin(α)sin(β) + cos(α);
allora l’area dell’ombra proiettata sul piano di terra è:
A = l × h cioè lato per altezza come prima definita, che è equivalente a scrivere
Giusto un esempio numerico con valori di angoli di rotazioni scelti a caso:
23° rotazione attorno all’asse x e 37° attorno all’asse z
f(22, 37) ≈ 1,4518 → area dell’ombra =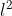
× 1,4518
è il caldo:
errata-corrige : f(23, 37) ≈ 1,4677→ area dell’ombra =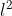
× 1,4677
Adesso ci siamo... l'area dell'ombra è sempre uguale all'area di una faccia moltiplicata per l'altezza.
Complimenti Andy!