14/10/22

(QI) Non basta la simmetria ****(*)

Categorie: Matematica Tags: equazione due variabili quiz soluzioni Scritto da: Vincenzo Zappalà Commenti:20

Ecco a voi una bellissima equazione nelle due variabili x e y:

$16^{x^{2}+ y} + 16^{y^{2} + x} = 1$

Risolverla per x e y numeri reali.

Attenzione 1: Questo problema non è banale, anche se potrebbe sembrarlo, a causa della simmetria degli esponenti.

Non basta la simmetria per arrivare a conclusioni affrettate! Ricordiamo, infatti, a titolo di esempio, che anche la seguente equazione è simmetrica in x e y:

x² + y² = 1

Ma essa non comporta solo la soluzione x = y = 1/√2... Infatti, ad esempio,

x = 1/2 e y = √3/2

Sono valori altrettanto soddisfacenti...

1/4 + 3/4 = 4/4 = 1

In conclusione: si vogliono tutte le possibili soluzioni.

Attenzione 2: Anche se, probabilmente inutili, sono vietati i logaritmi.

20 commenti

Alberto Salvagno

14/10/2022 at 10:25

Guarda che non si legge bene l'equazione iniziale
Vincenzo Zappalà

14/10/2022 at 10:39

Io la leggo bene...

16 elevato a x² + y ..., se preferisci 16^(x² + y)
Andy

14/10/2022 at 16:35

Caro Enzo,

ecco il mio ragionamento espresso in maniera schematica.

Per visualizzare l'immagine basta scrivere sulla barra degli indirizzi (tutto unito e senza spazi):

https:// prima di i.imgur.com/ZnSrbNl.png

Potrebbe essere l'unica soluzione in quanto il punto di coordinate x e y giace contemporaneamente sulle 2 parabole tangenti tra loro e sulla retta tangente ad entrambe, e questa retta è anche un asse di simmetria tra le due parabole stesse;

ma anche perché se si eguaglia la prima potenza a m/n e la seconda a 1 - m/n (con m e n diversi da 2 certi valori) sembra che non ci siano soluzioni.

Sempre con il beneficio del dubbio
Vincenzo Zappalà

14/10/2022 at 17:40

caro Andy,

temo che già dal primo passaggio tu scelga una certa soluzione che poi soddisfi la tangenza. Non mi sembra che tu determini che quella soluzione è l'unica, ma solo che è una soluzione. Devo ammettere che sono molto curioso delle vostre risposte, dato che, in effetti, la soluzione che è considerata ufficiale è ben più laboriosa. Volevo approfittare di voi per cercare di smontarla... io, per adesso, non ci riesco.
Fabrizio

15/10/2022 at 02:40

L'equazione ha una soluzione in x=y=-1/2 ottenibile ponendo x=y nell'equazione.

Sembrerebbe essere l'unica soluzione, anche se non sono riuscito ancora a dimostrarlo completamente,

La funzione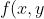 $f(x,y)=16^{x^2+y}+16^{x+y^2}-1$ ha un minimo in quel punto che si può verificare facendo le derivate rispetto a x ed y della funzione entrambe nulle in x=y=-1/2.

La funzione dovrebbe essere anche crescente allontanandosi dal x=y=-1/2, ma questo non sono ancora riuscito a dimostrarlo.
Vincenzo Zappalà

15/10/2022 at 08:26

Secondo me il vero problema è che noi abbiamo una somma, mentre sarebbe più comodo avere un prodotto, da poter maneggiare molto meglio. Almeno questa sembra la soluzione "ufficiale" senza bisogno di studiare la funzione.
Andy

15/10/2022 at 11:28

Prendiamola come un "esperimento":

se considero le 2 potenze al primo membro come funzioni singole e ne calcolo per ognuna di loro il rapporto tra le derivate parziali

$\frac{\frac{d}{dx}{(16^{x^2+y})}}{\frac{d}{dy}{(16^{x^2+y})}}$ = $2x$ $\frac{\frac{d}{dx}{(16^{x+y^2})}}{\frac{d}{dy}{(16^{x+y^2})}}$ = $\frac{1}{2y}$

eguagliandole: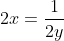 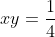$2x = \frac{1}{2y}$ → $xy=\frac{1}{4}$ che è un'iperbole e se mettiamo la condizione che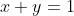 $x+y=1$

l'unica coppia x e y appartenente all'iperbole che soddisfa la condizione è x = y = 1/2 (graficamente è il punto di tangenza tra ramo d'iperbole del primo quadrante e retta).

Ponendo poi le singole potenze uguali a 1/2 :

$16^{x^2+y}=\frac{1}{2}$ → $y=-x^2-\frac{1}{4}$ con asse si simmetria y

$16^{x+y^2}=\frac{1}{2}$ → $y=\pm \sqrt{-x-\frac{1}{4}}$ con asse di simmetria x

già viste prima, che vengono soddisfatte per x = y = -1/2 (considerando il ramo in territorio negativo della seconda equazione). Praticamente per valori differenti da -1/2, la distanza tra il vertice di una parabola dall'origine e la distanza (complementare a 1) del vertice dell'altra parabola sempre dall'origine, fa si che le due parabole si posizionano in maniera tale da non toccarsi. Graficamente il tutto appare evidente, dimostrarlo matematicamente diventa difficoltoso...
Vincenzo Zappalà

15/10/2022 at 14:35

La soluzione che ho trovato non fa uso di geometria analitica, ma solo di algebra... Devo dire che è molto elegante e si risolve fin dall'inizio con una ... diseguaglianza! Non do ancora aiuti, ma il primo passaggio è fondamentale. Forza che ci riuscite sicuramente.
Andy

15/10/2022 at 16:32

Caro Enzo,

mi hai fornito un assist illuminante!

Se denomino le 2 potenze

$16^{x^{2}+ y} = a$ e $16^{x + y^2} = b$ posso scrivere l'equazione principale come: $a+b=1$

Ma se divido ambo i membri per 2, otterrò un equazione equivalente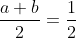 $\frac{a+b}{2}=\frac{1}{2}$

Ora, (a + b) / 2 è la media aritmetica di a e b che, rimanendo in termini di medie, dovrebbe essere sempre maggiore della relativa media geometrica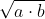 $\sqrt{a \cdot b}$ per ogni a e b reale positivo

(ad esempio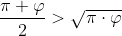 $\frac{\pi+ \varphi }{2} > \sqrt{\pi \cdot \varphi}$ ).

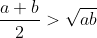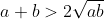
La dimostrazione è semplice: $\frac{a+b}{2} > \sqrt{ab}$ → $a+b > 2 \sqrt{ab}$

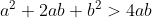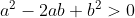
ed elevando al quadrato $(a+b)^2 > 4ab$ → $a^2+2ab+b^2 > 4ab$ → $a^2-2ab+b^2 > 0$

ovvero $(a-b)^2 > 0$ che è sempre vera per ogni a e b reali escluso lo zero, tranne che in un caso solo: a = b

che annulla il primo termine della disequazione.

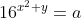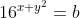
Allora se applico il caso unico all'equazione principale si avrà che: $16^{x^{2}+ y} = a$ e $16^{x + y^2} = b$

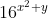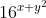con a = b → $16^{x^{2}+ y}$ = $16^{x + y^2}$ .

Ma siccome la loro somma deve dare 1, le due potenze devono essere "fifty-fifty" ovvero 1/2 e 1/2

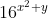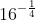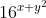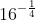
quindi: $16^{x^{2}+ y}$ = $\frac{1}{2}$ = $16^{-\frac{1}{4}}$ e $16^{x + y^2}$ = $\frac{1}{2}$ = $16^{-\frac{1}{4}}$

Per cui:

che riprende, parzialmente, il mio primo post.

Avrei trovato anche una soluzione di tipo "iperbolico", vediamo se riesco a postarlo.
Vincenzo Zappalà

15/10/2022 at 19:08

lo sapevo Andy che ce l'avresti fatta!
Andy

16/10/2022 at 01:21

Ecco la soluzione alternativa derivante da un approccio analitico-"iperbolico":
Fabrizio

16/10/2022 at 20:36

Visto che Enzo lascia aperto il quiz, approfitto per proporre una versione della soluzione che è sulla scia aperta da Andy (complimenti ad Andy). Nella soluzione c'è un un mio dubbio che spero Enzo sciolga.

Scelgo di definire in modo leggermente diverso a e b per risparmiare qualche passaggio:

$a^2=16^{x^2+y}\;\;\; b^2=16^{y^2+x}$ quindi $a^2+b^2=1$

considero che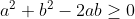 $a^2+b^2-2ab\geq 0$ da cui 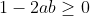$1-2ab\geq 0$ quindi

$\large \mathbf{ab\leq \frac{1}2{}}$ . Nel ragionamento fatto finora non c'è niente che porti a concludere che valga solo l'uguaglianza, vale a dire a=b, almeno io non sono riuscito a vederlo. Questo è il mio dubbio.

L'unico modo che ho trovato è procedere con l'analisi esplicitando a e b, cioé:

$4^{x^2+y}\; 4^{y^2+x}=4^{x^2+y+y^2+x}\leq 4^{-\frac{1}{2}}$ da cui $x^2+y+y^2+x\leq -\frac{1}{2}$ , cioè

$\mathbf{x^2+y+y^2+x+\frac{1}{2}\leq 0}$ . In questo caso specifico si tratta della somma di due quadrati

$(x+\frac{1}{2})^2+(y+\frac{1}{2})^2\:\leq 0$ . Solo qui riesco ad affermare che $\mathbf{x=-\frac{1}{2}}$ e $\boldsymbol{\mathbf{}y=-\frac{1}{2}}$ e che a=b.
Vincenzo Zappalà

17/10/2022 at 08:25

Il succo di tutto è la disuguaglianza (a+b)/2 ≥ √(ab). Ma, come dici tu, si deve maneggiare √ab in modo da dimostrare che esso deve essere ≥ 1. Esplicitando ab si perviene con passaggi abbastanza banali a

1 ≥ 2√(ab) ≥ 1

Da cui l'uguaglianza finale in cui figura un prodotto di due fattori che può essere uguale a 1 solo se il loro esponente è uguale a 0.

4⁽^{x +}^0.5)²∙ 4⁽^{y +}^0.5)² = 1.

Se riesco oggi pubblico la soluzione che non si discosta da quella di Andy.
Andy

17/10/2022 at 09:01

Giusta l'osservazione di Fabrizio e ineccepibile lo svolgimento algebrico.

Però se so che la media aritmetica dei due termini è 1/2 e che la media geometrica deve essere ≤ 1/2, allora deve essere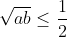 $\sqrt{ab} \leq \frac{1}{2}$ che elevando al quadrato diventa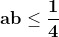 ${\bf ab\leq \frac{1}{4}}$

Ma so anche che a + b = 1, ovvero b = 1 - a, per cui sostituendo nell'ultima disequazione diventa

$a(1-a) \leq \frac{1}{4}$ che sviluppando e cambiando di segno diventa $a^2 - a + \frac{1}{4} \geq 0$ → $\left ( a - \frac{1}{2} \right )^2 \geq 0$

che è sempre vera tranne che per a = 1/2 dove si annulla.
Fabrizio

17/10/2022 at 11:17

Andy, non riesco a seguire la tua ultima affermazione, che è il punto dove mi sono fermato anche nel mio ragionamento.

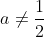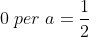Se $(a-\frac{1}{2})^2\geq 0$ è sempre vera, positiva per $a\neq \frac{1}{2}$ o $0\; per \; a = \frac{1}{2}$ , cosa obbliga a scegliere il solo a=1/2.

D'altra parte, se fosse vero che dobbiamo scegliere solo a=1/2, sarebbe come dire che in a+b=1 a deve essere 1/2.

In realtà può essere 1/2, ma può essere anche qualsiasi altro numero reale.
Vincenzo Zappalà

17/10/2022 at 15:41

Sono contento della discussione che è sorta... Spero entro stasera di inserire la mia versione e magari si accende ancora di più
Andy

17/10/2022 at 15:59

Caro Fabrizio, io la vedo così:

partiamo dall'assunto che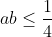 ${ab\leq \frac{1}{4}}$ e che a + b = 1, (e quindi a = 1 - b e b = 1 - a) ovvero sia a che b sono sottoposti al vincolo della complementarità ad 1, per cui se prendo come riferimento a deve essere:

0 < a < 1 e parimenti 0 < b < 1 con b complementare ad 1; se prendo come riferimento b

0 < b < 1 e parimenti 0 < a < 1 con a complementare ad 1.

Allora, nella disequazione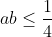 ${ab\leq \frac{1}{4}}$ prendendo come riferimento a, posso scrivere:

${a(1-a)\leq \frac{1}{4}}$ → $a-a^2-\frac{1}{4} \leq 0$ → $- \left ( a - \frac{1}{2} \right )^2 \leq 0$ ovvero $\left ( a-\frac{1}{2} \right )^2 \geq 0$

lo stesso se prendo come riferimento b, otterrò $\left ( b-\frac{1}{2} \right )^2 \geq 0$

Ora, se i singoli quadrati sono ≥ $0$ , lo sarà anche la loro somma:

$\left ( a-\frac{1}{2} \right )^2$ + $\left ( b-\frac{1}{2} \right )^2$ ≥ $0$ che sarà nulla solo se a e b sono contemporaneamente nulli cioè uguali ad $\frac{1}{2}$

Lo stesso avviene anche se prendo a e b singolarmente:

$\left ( a-\frac{1}{2} \right )^2$ + $\left ( 1 - a -\frac{1}{2} \right )^2$ = $0$ solo per $a = \frac{1}{2}$

$\left ( b-\frac{1}{2} \right )^2$ + $\left ( 1 - b -\frac{1}{2} \right )^2$ = $0$ solo per $b = \frac{1}{2}$

È come se geometricamente considerassi la funzione:

$f(a)=a(1-a)=-a^2 + a$ con la variabile a nell'intervallo $]0, 1[$ ,

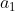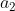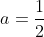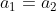scelto un punto qualunque $a_1$ e il suo complementare ad 1 $a_2$ , entrambi diversi da $\frac{1}{2}$ , le rette tangenti nei due punti presentano pendenze differenti di valore e opposte di segno, ma nel punto di massimo $f'(a) = -2a + 1$ che si annulla per $a = \frac{1}{2}$ , in $a_1=a_2$ le due tangenti si allineano e coincidono, con pendenza nulla.

Discorso uguale e simmetrico per $f(b)=b(1-b)=-b^2 + b$
Fabrizio

17/10/2022 at 19:02

Andy, stai dicendo che a+b=1 con a e b positivi ammette la solo soluzione a=b=1/2?

Ovviamente non è così. Trai tu le conclusioni.

Nel tuo ragionamento è tutto corretto, ma manca la dimostrazioni che $(a-\frac{1}{2})^2+(b-\frac{1}{2})^2$ debba essere 0 e solo 0.

Questa dimostrazione dipende dal contenuto di a e b, non è possibile in generale. Ad esempio non è vera per a=1/3 b=2/3, eppure 1/3+2/3=1.
Andy

17/10/2022 at 20:08

No, sto dicendo tutt'altro:

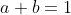se nell'intervallo $]0 , 1[$ consideri solo ed isolatamente la condizione $a+b=1$ , trovi infiniti valori che la soddisfano, ma se la stessa condizione 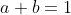$a+b=1$ viene vincolata a sua volta dalla condizione 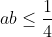$ab\leq \frac{1}{4}$ cioè li poni a sistema, l'unica coppia di valori che soddisfa contemporaneamente le 2 equazioni è

$a=b=\frac{1}{2}$

È vero che 1/3 + 2/3 fa 1, ma non è vero che (1/3)(2/3) = 1/4.

Il prodotto di tutte le coppie di valori, reciprocamente complementari a 1, nel citato intervallo, è minore di 1/4.

Prova a trovare, nello stesso intervallo, una coppia che contemporaneamente dia 1 come somma e 1/4 come prodotto.
Fabrizio

17/10/2022 at 21:53

Evidentemente non sono riuscito a comunicare dove, a mio parere, risiede il problema.

Comunque, ora Enzo ha pubblicato la soluzione dettagliata del problema. Credo che questa soluzione possa fare da riferimento per tutti.

Lascia un commento Cancel Reply

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.