Ho letto questo articolo sulle matrici di rotazione, scritto da quello scriteriato del Bernardi, che mi ha lasciato un po' stupito. Incredibile che uno come lui possa avere avuto questo lampo di genio, anche se non sarà di sicuro tutta farina del suo sacchetto.

Certo che questa cosa casca a fagiolo anche per trovare i punti di una curva diurna per una meridiana, che è sempre un bel problema.

Impostazione della soluzione

Basta partire da una posizione iniziale della meridiana “facile”, per la quale si sa dove cade l'ombra della punta dello stilo e poi, studiando le rotazioni necessarie per passare alla vera posizione in cui va messo il quadrante, si fanno i calcoli con quelle tabelle (che lui chiama pomposamente “matrici di rotazione”) e si trovano le coordinate giuste.

Per farmi capire meglio vi propongo questa figura...

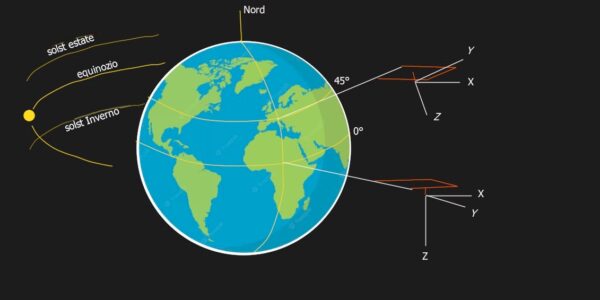
Vedete la Terra nello spazio (ma questo lo avrete già intuito) con il suo bel Equatore alla latitudine 0° e quel parallelo a 45°, tanto per fare un esempio che sia vicino a Cuneo.

Sulla sinistra c'è il Sole con la traiettoria che all'equinozio gira proprio intorno all'equatore. Poi ho messo anche le traiettorie più sopra e più sotto che sono quelle dei solstizi in estate e in inverno. Così si capisce che nel corso dei mesi cambia l'angolo di “declinazione” sotto cui ci appare la nostra stella.

Adesso guardate sulla destra della figura e vedrete due sistemi di riferimento con i tre assi xyz. Quello sull'equatore è centrato sulla punta dello stilo conficcato nella parete verticale (contorno rosso) costruita all'equatore. L'altro sistema xyz è invece centrato sulla punta dello stilo che è piantato sulla parete verticale che si trova a Cuneo, ben 45° di latitudine sopra l'equatore.

Ecco fatto.

Ammettiamo che siete a Cuneo alle ore 14 del giorno del solstizio di estate.

Guardate l'ombra dello stilo infisso sul muro, perfettamente verticale e perfettamente orientato verso sud, e vi domandate perché quel punto cade proprio lì dove si trova.

Questa è la immagine di quello che vedete...

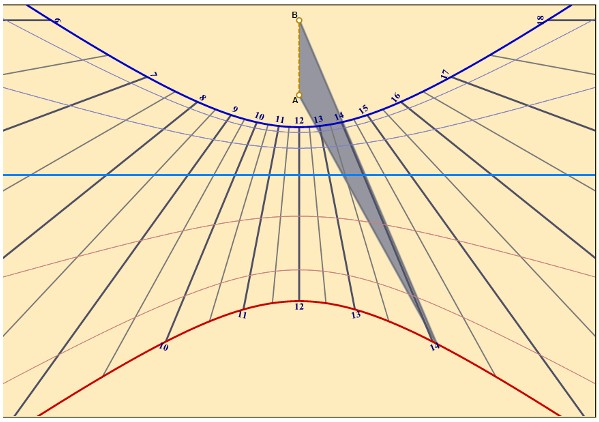
Attenzione: l'ora segnata dalla nostra meridiana è proprio l'ora solare e non l'ora “legale” che adottiamo ostinatamente da tanti anni durante l'estate.

Se invece di essere a Cuneo in quel particolare momento, vi trovaste 45° più a Sud lungo lo stesso meridiano e fossero le ore 12 del giorno dell'equinozio di primavera, sarebbe tutto più semplice.

Infatti, essendo il giorno dell'equinozio, la declinazione del Sole sarebbe nulla e, essendo mezzogiorno, il sole lo vedreste proprio a Sud e, infine, stando all'equatore, lo stilo risulterebbe parallelo all'asse terrestre (mentre a Cuneo non lo è).

In questo frangente l'immagine che vedreste sulla parete verticale sarebbe quest'altra...

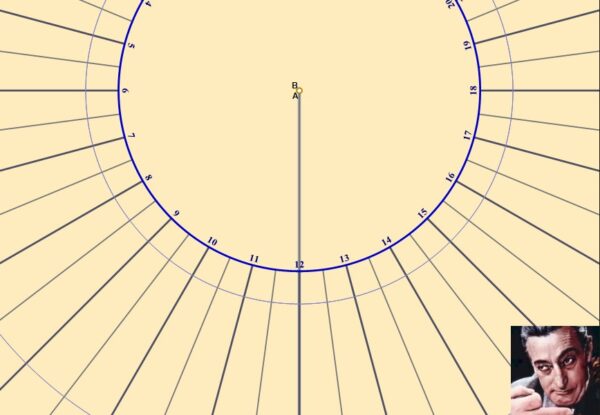
(Ho fatto un selfie perché altrimenti potreste sospettare che me la sono inventata)

In verità la “foto” è stata scattata un poco prima dell'equinozio di primavera perché, dopo quel momento per 6 mesi, diconsi SEI, il sole illumina l'altro lato della parete e dalla nostra parte rimane tutto in ombra. Perbaccolina! Pensateci su.

Gli angoli significativi, che sono differenti nelle due situazioni, sono tre:

la declinazione δ , l'angolo orario H e la latitudine φ

Per passare dalla declinazione = 0° dell'equinozio di primavera a quella = 23,43° del solstizio d'estate, occorre una rotazione in senso orario di 23,43° attorno all'asse X.

Dato che la convenzione assegna valori positivi alle rotazioni in senso antiorario, diciamo che una rotazione oraria equivale a una antioraria preceduta dal segno negativo. Quindi la nostra rotazione la dobbiamo scrivere con il meno: δ = - 23,43° attorno all'asse Z.

Per l'arco diurno, che è l'angolo che misuriamo avendo come riferimento il mezzogiorno, vale il segno positivo per il pomeriggio e negativo per la mattina. In tal modo è rispettata la suddetta regola del senso di rotazione antiorario.

Dato che in 24 ore la terra gira di 360°, in ciascuna ora l'arco coperto è di 15° e per passare dalle ore 12 alle ore 14 la rotazione sarà: H = 30° attorno all'asse Y.

Resta da valutare la differenza di orientamento rispetto al Nord. Non è altro che la differenza di latitudine, che aumenta ruotando in senso antiorario rispetto l'asse X.

La rotazione da eseguire sarà quindi: φ = 45° attorno all'asse X.

Attenzione... non possiamo associare in una unica rotazione cumulativa le due rotazioni attorno all'asse X perché non sono consecutive ma intervallate da una rotazione attorno Z.

Applichiamo le matrici di rotazione

Concludendo, utilizzerò i simboli delle matrici di rotazione per rappresentare le operazioni sul vettore da rigirare in questo modo:

R^x_-23,43° * V1 = V2

R^z_30° * V2 = V3

R^x_45° * V3 = V4

Ragioniamo ora sulle componenti del vettore “facile” che abbiamo scelto come punto di partenza, ossia V1. La proiezione dell'ombra non ha alcuna componente sugli assi X e Z, ma è parallela al loro piano. Il raggio colpisce la punta dello stilo e l'ombra cade lungo la direzione -Y. Scriviamo il vettore in forma di tabella:

Vettore 1 inizio

0

-1

0

Eseguiamo la prima rotazione di -23,43° attorno a X. La matrice di rotazione va moltiplicata per il Vettore 1

Matrice di rotazione Rx-23,43°	Vettore 1	Vettore 2
1 0 0	0	0
0 cos(-23,43) - sen(-23,43)	-1	- cos(-23,43)
0 sen(-23,43) cos(-23,43)	0	- sen(-23,43)

Ora, calcolati i valori delle componenti del Vettore 2, passiamo alla seconda rotazione di 30° attorno a Z

La matrice di rotazione va moltiplicata per il vettore 2

Matrice di rotazione RZ30°	Vettore 2	Vettore 3
cos(30) - sen(30) 0	0	0,918 sen(30)
sen(30) cos(30) 0	-0,918	-0,918 cos(30)
0 0 1	0,398	0,398

Infine, calcolati i valori delle componenti del Vettore 3, passiamo alla terza rotazione di 45° attorno a X.

La matrice di rotazione va moltiplicata per il vettore 3

Matrice di rotazione Rx45°	Vettore 3	Vettore 4
1 0 0	0,459	0,459
0 cos(45) - sen(45)	-0,796	-0,796 cos(45) -0,398 sen(45)
0 sen(45) cos(45)	0,398	-0,796 sen(45) + 0,398 cos(45)

Restano solo da calcolare le componenti del Vettore 4 finale.

Vettore 4

0,459

-0,562 -0,281

-0,562 +0,281

Vettore 4

0,459

-0,843

-0,281

Il raggio di sole che colpisce la punta dello stilo perpendicolare alla parete verticale a Cuneo, alle ore 14 del giorno del solstizio estivo, è adagiato su una retta che è individuata da queste componenti sugli assi cartesiani XYZ.

Abbiamo trovato i coseni direttori, come li definisce nel suo articolo il famigerato Bernardi.

Notate che la somma dei loro quadrati vale proprio 1, così come era per il vettore iniziale.

Il nostro obiettivo, ricordiamo, è di trovare le coordinate del punto ombra sulla parete verticale, qui a Cuneo.

Si tratta di trovare l'intersezione tra questa retta passante per l'origine degli assi e il piano XY che giace alla distanza G= - altezza dello stilo o gnomone.

Le equazioni parametriche^● della retta sono pertanto le seguenti:

x= 0,459 t

y= -0,843 t

z= -0281 t

mettendo a sistema il piano xy di equazione z = -G possiamo ricavare il parametro t

z = -0,281 t = -G da cui t = G/0,281 da sostituire in x(t) e y(t)

x= 0,459 G/0,281

y= -0,843 G/0,281

x= 1,633 G

y= - 3 G

Ecco fatto, queste sono le coordinate che cercavamo.

Conclusioni

Se riguardate qui sotto la “foto“ della meridiana a Cuneo, ritrovate le proporzioni tra X e Y e l'attribuzione del segno positivo a X e negativo a Y. Il punto A è l'origine delle misure .

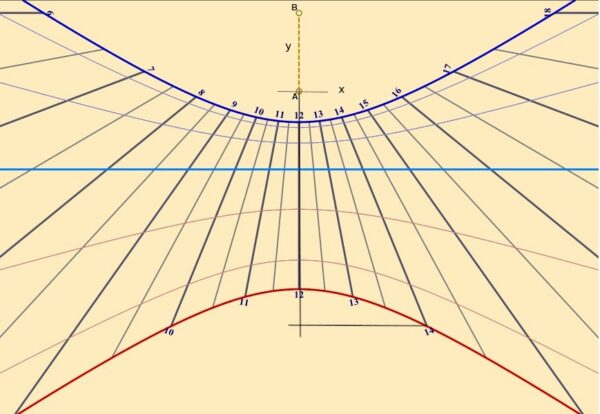
• per un ripasso sulle equazioni parametriche, niente di meglio che questo articolo del blog.

Il procedimento visto per un singolo punto può essere facilmente esteso a tutti i punti che ci interessano: basta fissare delta e variare la H e avremo una iperbole diurna, o viceversa tenere fisso H e variare delta e avremo una retta oraria. Possiamo anche trovare i punti dell'analemma (basta modulare delta e H secondo l'equazione del tempo). E se vogliamo calcolare la meridiana con una latitudine diversa o uno stilo più grande non ci vuole nulla.

La cosa più ragionevole è usare per questi calcoli una medesima routine che esegua i prodotti tra matrici e vettori in modo automatico. Basterà assegnare l'angolo di rotazione con l'opportuno segno e indicare l'asse a cui è riferito per personalizzare l'operazione.

Se la parete non fosse orientata a Sud ma presentasse una propria declinazione verso est o verso ovest, basterà aggiungere una ulteriore rotazione attorno all'asse Y (sempre considerando che le rotazioni antiorarie hanno segno positivo)

Se poi la parete non fosse verticale ma inclinata occorrerà una rotazione finale dell'angolo di inclinazione per tenere conto del “pendio” del muro. Sarà una rotazione attorno all'asse X che ci consegnerà le giuste coordinate delle linee del reticolo rette-iperboli.

Ma non potreste scegliervi un muro meno problematico?

Un momento, non cambiate canale … Il Bernardi mi ha intimato di scrivere quanto segue:

Il contenuto di questo articolo e del precedente “Rotazioni di Vettori” si ispira al lavoro di Tonino Tasselli, presentato nell'aprile 2005 al XIII Seminario Nazionale di Gnomonica, con il titolo “Applicazioni del calcolo vettoriale alla gnomonica” (fonte: http://www.ilpaesedellemeridiane.com/seminario/atti/PDF/Relazione%2024.pdf) Si consiglia a tutti coloro che volessero approfondire con un approccio più serio questo argomento, di leggere la relazione di Tasselli, con la certezza che ne trarranno grande  piacere.

Per una volta sono d'accordo con lui

Cerea!