Categorie: Matematica
Tags: cerchi olimpici configurazioni possibili quiz
Scritto da: Vincenzo Zappalà
Commenti:38
(Q) Verso le Olimpiadi ***/****/******...
Ci stiamo nuovamente avvicinandoci alle Olimpiadi (covid permettendo) e inganniamo il tempo guardando i famosi cinque cerchi che caratterizzano il simbolo olimpico. Semplice... cinque cerchi uguali che si intrecciano come mostra la figura che segue:

Basterebbe, però, molto poco per cambiare configurazione, compresa quella con i cerchi tutti separati tra loro.
Iniziamo il nostro gioco (e il vostro QUIZ).
I cerchi possono essere di qualsiasi dimensione ma devono sottostare ad alcune REGOLE:
1) Non si accettano cerchi tangenti tra loro o cerchi degeneri in una retta.
2) Si considerano tutti i cerchi su uno stesso piano e non interessa se uno passa sopra o sotto l'altro come nella bandiera olimpica. Basta che si incontrino oppure no.
3) Tre o più cerchi cerchi non possono intersecarsi in un solo punto.
Le configurazioni non ammesse sono rappresentate in Fig. 1
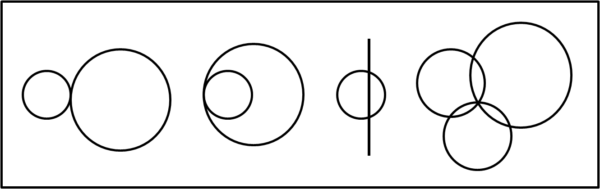
4) Si intende per configurazione, il modo con cui i cerchi si incontrano oppure no. Ad esempio, qualsiasi siano i raggi, se la configurazione mostra un cerchio dentro l'altro viene considerata la stessa. Le configurazioni si riferiscono a posizioni reciproche generali.
Cominciamo con il semplice caso di due cerchi
Esistono solo TRE configurazioni, come mostra la Fig. 2:
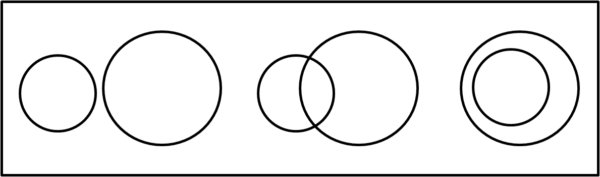
Il prossimo passo è quello di lavorare con tre cerchi e vi chiedo:
Quanti e quali sono le configurazioni possibili?
Se riuscite in questo esercizio, potete sempre provare con quattro cerchi... e vi meritereste di partecipare alle Olimpiadi.
I più volenterosi potrebbero anche provare con cinque cerchi, ossia modificare proprio la configurazione relativa alle Olimpiadi. Vi posso assicurare che se arrivaste a questa soluzione una medaglia olimpica non ve la toglierebbe nessuno!
NOTA BENE:
La soluzione del quiz impone un disegno. Potete anche farlo a mano libera e, qualora non sappiate come inserirlo nel commento, potete scannerizzarlo o fotografarlo e inviarlo a Daniela (infinitoteatrocosmo@gmail.com) che provvederà.
QUI la prima parte della soluzione






38 commenti
Da ciascuna delle 3 configurazioni basate su due cerchi, ricavo le possibili varianti aggiungendo il terzo cerchio.
Controllo di non avere nuove configurazioni duplicate.
Ecco la figura :
dalla configurazione "a" ricavo 6 possibili varianti ( a1 - a6)
dalla "b" ne ricavo 4 ( b1 - b4)
dalla "c" ne ricavo "4" (c1 - c4)
Confrontando le 14 configurazioni vedo però che c3 conicide con a5 e c4 coincide con a4
Quindi le configurazioni distinte sono solo 12.
Potrebbero esserci ulteriori riduzioni di queste 12 se invece di osservare l'aspetto del disegno si ragiona solo sul numero di intersezioni tra i cerchi, perché in questo caso ci possono essere ulteriori "equivalenze". Quest'ultimo punto non mi è del tutto chiaro.
Ad esempio, la ulteriore possibile variante b5 , in figura:
Va considerata equivalente, oppure no alla variante b1 (in cui il cerchio aggiunto non ha punti di contatto con i primi due dato che li circonda entrambi) ?
Se andasse considerata come un caso diverso, allora avremmo 13 configurazioni.
Seguendo il ragionamento che riporto sotto, a me vengono 10 possibili configurazioni.
Considero le possibili configurazioni di 2 cerchi alla volta di fig.2.
Possono essere disgiunti (D), intersecanti (I) o sovrapposti (S).
Prendendo 2 cerchi alla volta dei 3 (che chiamo C1,C2 e C3) devo considerare la configurazione di C1-C2, C1-C3 e C2-C3. Vale a dire, devo assegnare una delle 3 configurazioni (D,I,E) a ciascuno con la possibilità di assegnare anche più volte la stessa configurazione.
Ad esempio C1-C2=D, C1-C3=D, C2-C3=I o C1-C2=I, C1-C3=D, C2-C3=S. Per brevità indico queste configurazioni con le tre lettere giustapposte. Le due dell'esempio sono D I I e I D S.
Se non ho capito male, dobbiamo considerare i cerchi indistinguibili tra loro. Di conseguenza non conta l'ordine con il quele le lettere appaiono nella stringa. Quindi D I I, I D I o I I D non sono da considerare configurazioni distinte. Inoltre conta se avvengono le intersezioni tra due cerchi, ma non conta dove avvengono.
In conclusione le configurazioni distinte sono le combinazioni (non conta l'ordine) con ripetizione di tre tipi di oggetti (D I S) a 3 a 3.
Se valgono le ipotesi fatte sopra, il risultato è 10.
Cercando di introdurre un metodo per non lasciarsi sfuggire qualche configurazione si può agire aumentando progressivamente il raggio del terzo cerchio, collocando il suo centro ora nella parte di piano esterno ai cerchi, ora nella parte interna ad essi.
Partendo dai tre schemi possibili con due cerchi genero le tre figure seguenti per tipo A tipo B tipo C.
All'interno di ciascun TIPO creo i cerchi con centro esterno e poi aggiungo quelli con centro interno cercando di evitare ripetizioni di casi equivalenti.
Nella seconda figura, all'interno della famiglia B, ad esempio, noto che B3 = B8, quindi dovrò eliminare B8 perché è una ripetizione.
Allo stesso modo, nella terza figura, all'interno della famiglia C, noto C3 = C8, quindi anche qui andrà eliminato C8 che rappresenta una ripetizione.
Passo poi a confrontare a coppie le tre famiglie A B C individuando altre ripetizioni, come nei casi B2= A7 e anche C1 = A6. Dovrò così eliminare B2 e C1.
Per avere il numero delle combinazioni distinte dovrò sottrarre al totale complessivo di 23 configurazioni le quattro "doppie" che ho individuato ( B8, C8, B2 e C1) e avrò pertanto 19 casi.
Ma, anche ammesso di avere fatto un conteggio corretto, senza omettere alcune configurazioni e senza lasciarsi sfuggire alcuna duplicazione, resta sempre da chiarire come valutare l'equivalenza: in generale due configurazioni che appaiono diverse per il modo in cui sono disposti i cerchi, sono o non sono equivalenti se hanno lo stesso numero di intersezioni?
Giusto per fare un esempio concreto... La configurazione B5 ha due cerchi che si intersecano ed un cerchio che li contiene. La configurazione B6 ha i medesimi cerchi che si intersecano e un cerchio inserito nella zona della loro intersezione. Quindi B5 e B6 sono simili perché presentano ambedue un cerchio che non interseca gli altri due, ma questo cerchio in un caso "contiene" , nell'altro caso "è contenuto". Sono due configurazioni distinte oppure vanno considerate come la medesima configurazione?
La difficoltà incontrata partendo dalle tre disposizioni iniziali di due cerchi per trovare le configurazioni possibili con l'aggiunta del terzo, diventerà molto maggiore quando si andrà ad aggiungere il quarto cerchio perché gli schemi di partenza ( quelli con tre cerchi) saranno ben più numerosi. Oltre al problema di valutare a priori quanti risultati aspettarsi (invece di contarli dopo aver generato le figure come ho fatto io) aumenta di ancora di più la difficoltà di produrre tutte le figure e, soprattutto, di eliminare le duplicazioni quando si confrontano a coppie le famiglie di configurazioni, perché il numero di confronti da fare cresce a dismisura.
E' quindi probabile che l'approccio da seguire debba essere diverso e più efficiente di quello esposto.
Per adesso rispondo a Mau sulla possibile uguaglianza di due configurazioni...
Queste sono diverse. Per comprendere bene la diversità, conviene stabilire per bene le caratter4istiche di ogni singola configurazione.
La prima ci dice che vi è un cerchio i cui punti appartengono completamente all'intersezione degli altri due. La seconda ci dice che vi è un cerchio che contiene completamente gli altri due che si intersecano tra loro. Due definizioni completamente diverse...
Attenzione che, definendo per bene le loro caratteristiche alcune configurazioni, apparentemente diverse diventano uguali...
L'impostazione di Fabrizio risponde perfettamente alla esigenza di poter valutare a priori quante configurazioni si possono realizzare. Tuttavia la definizione di "configurazioni distinte" non sembra coincidere con quella del problema, dato che non viene generata la configurazione in cui esiste un cerchio completamente inserito nella intersezione degli altri due.
Ho provato a mappare le 13 configurazioni che avevo ipotizzato nel primo (e secondo ) commento con quelle generate da Fabrizio, in questa figura
Le 10 configurazioni di Fabrizio sono tutte presenti.
In aggiunta c'è la configurazione b5 che, visto il commento di Enzo, deve essere considerata.
Poi ci sono altre due configurazioni ( la b2 e la b3 ) che potrebbero essere equivalenti alla b4 ( III per Fabrizio)
Infatti, come nella b4, il nuovo cerchio (rosso) interseca ambedue i cerchi precedenti. Però, mentre nella b3 il cerchio rosso passa nella loro zona di intersezione (come vediamo nella b5), nella configurazione b2 la zona di intersezione non viene attraversata. In base a questa diversità sembrerebbe di dover mantenere valida la b2. Per contro si dovrebbe scartare la b3 (duplicazione di b4) .
In tal caso le configurazioni diverse e distinte diventerebbero 12.
E' necessario come prima cosa enunciare i criteri di equivalenza, poi credo che il metodo di Fabrizio sia quello più conveniente soprattutto perché è estendibile anche al caso di 4 , 5 , N cerchi.
Invece di derivare le configurazioni per i tre cerchi da quelle già note per i due cerchi (aggiungendo il terzo) si può procedere generando le possibili configurazioni di tre cerchi con nessuna intersezione, poi con una , poi con due e infine con tre, come nella figura seguente.
Mi sembra che in questo modo sia più semplice arrivare al risultato. Occorre però trovare il modo di quantificare a priori il numero di configurazioni in ciascuno di questi quattro gruppi.
Procedendo nel modo indicato nel precedente commento ho trovato per 4 cerchi questa distribuzione:
N. intersezioni
N. configurazioni
0
7
1
7
2
12
3
7
4
3
5
2
6
1
In totale sono 39 configurazioni, Ma potrei averne trascurata qualche altra.
Il disegno di queste 39 varianti è piuttosto complesso e aspetto a pubblicarlo.
Pensavo che utilizzando una tabella sarebbe stato più chiaro, ma vedo che funziona in modo strano.
riscrivo in forma diversa ...
N intersezioni 0 1 2 3 4 5 6
N configurazioni 7 7 12 7 3 2 1
Caro Mau,
prima di passare ai 4 cerchi, bisognerebbe completare le configurazioni dei tre cerchi...
Non intendo risolvere ora il problema per i 4 cerchi.
Mi serve solo osservare come cresce il numero delle configurazioni per capire se esiste una regola generale per prevedere il loro numero e poterla applicare al caso dei tre cerchi.
Ho aggiornato la collezione di configurazioni aggiungendo due varianti nella colonna delle 3 intersezioni.
Sono distinguibili per i cerchi in azzurro.
La penultima configurazione mi sembra effettivamente necessaria, ma sull'ultima ho la sensazione che si tratti di un duplicato simile alla seconda nella stessa colonna, dato che in tutte e due il cerchio rosso interseca gli altri due e attraversa la loro zona di intersezione. L'unica differenza è che in questo caso contiene i due punti di intersezione, invece di uno solo
Escludendo quest'ultimo disegno le configurazioni distinte sono 13. Tenendone conto diventano 14.
Manca ancora un metodo per prevedere il numero di configurazioni senza fare alcun disegno.
Vedo ora che l'ultima e la penultima configurazione (colonna delle tre intersezioni) sono identiche.
Manca invece una configurazione che mi sembra diversa da ogni altra. Ecco l'aggiornamento in cui compare all'ultimo posto.
Mau, l'ultima che hai inserito mi sembra uguale a b2...
Carissimi,
per non incorrere in doppioni... consiglierei di scrivere, per ogni configurazione, le caratteristica salienti in modo che si possano confrontare tra di loro. Ad esempio, la b2 di Mau raffigura due cerchi che si intersecano e un terzo che l'interseca entrambi e contiene completamente l'intersezione dei primi due. Anche l'ultima corrisponde esattamente a questa definizione.
Non penso proprio che si possano calcolare preventivamente... o -almeno- sarebbe una grande scoperta.
Osservando la figura b2 i due cerchi neri si intersecano e il cerchio rosso non passa nella zona di intersezione.
L'ultima configurazione presenta due cerchi azzurri che si intersecano e il cerchio rosso passa nella zona di intersezione, quindi potrei pensare che non sono la stessa configurazione.
Tuttavia, se analizzo ambedue le configurazione in tre modi diversi, a seconda del punto di vista di ciascun cerchio, trovo tre letture identiche
Quindi hai ragione dicendo che l'ultima figura duplica la b2 e va tolta.
Per fare un contro esempio, confronto l'ultima figura con la b4 e vedo che nella b4 ciascun cerchio taglia la zona di intersezione degli altri due. Viceversa nell'ultima configurazione ciò avviene solo in due casi (esiste una zona di intersezione, quella tra il cerchio rosso e quello azzurro di destra, non tagliata) Quindi ho due configurazioni diverse perché non tutte le tre letture concordano.
Se i cerchi fossero quattro, facendo il confronto tra due figure, dovrei trovare concordanza tra i quattro punti di vista ( descritti da ciascun cerchio ) dell'una e dell'altra configurazione.
Il fatto che non si possa predire il numero da un lato mi conforta ( nella domanda posta "quante e quali sono le configurazioni possibili?" essendo chiesta come prima cosa la quantità, avevo inteso che fosse prevedibile).
Dall'altro lato capisco che la risposta a "quante sono" la si può dare solo contando le figure prodotte dopo avere eliminato i duplicati. Questo mi fa pensare di avere davanti un lavoro "certosino", soprattutto per il proliferare delle configurazioni con l'aumentare del numero di cerchi.
Per rendere sistematica la produzione delle configurazioni occorre un metodo di generazione delle figure.
Si può pensare di partire dalla precedente "famiglia" (con un cerchio in meno) aggiungendo il nuovo cerchio con tutte le possibili varianti, Oppure, a prescindere dalla precedente famiglia, creare configurazioni con il numero di cerchi desiderato, raggruppandole "a pari numero di intersezioni", come ho fatto nell'ultima figura.
Per ogni configurazione occorre dare le N descrizioni del punto di vista di ciascun cerchio al fine di confrontarla con le altre ed eliminare i duplicati.
Ma la cosa migliore sarebbe trovare il modo di non generare alcun duplicato già nel procedimento di costruzione delle figure.
Ecco un esempio che crea qualche dubbio ...
Nelle tre figure A B C i punti di vista del cerchio rosso sono identici. Altrettanto per il cerchio nero
Viceversa il punto di vista del cerchio blu è diverso nei tre casi perché in A non passa per l'intersezione degli altri due cerchi, mentre in B e in C passa.
Però, mentre in B passa una sola volta, in C passa per due volte.
Cosa è rilevante ? il passaggio - non passaggio oppure il numero di passaggi ?
In un caso dovrei scartare una delle tre figure, nell'altro dovrei tenerle tutte come casi diversi.
la prima figura è quella classica dei tre cerchi che si intersecano (b4). Le altre due sono diverse:
1)Due cerchi si intersecano, il terzo interseca la loro intersezione ed è contenuto nella loro unione
2) Due cerchi si intersecano e il terzo contiene la loro intersezione
Considera due cerchi intersecantesi e inseriamo il terzo all'interno della loro intersezione (prima config.). Poi ingrandiamo il terzo cerchio in modo che intersechi l'intersezione, ma rimanga confinato all'interno dell'unione dei due cerchi (1); Il terzo s'ingrandisca ancora contenendo l'intersezione dei primi due (2) ; il terzo cresca ancora e contenga i primi due. 4 casi ottenuti solo con l'ingrandimento del terzo..
La configurazione "classica" non impone che il cerchio contenga l'intersezione degli altri due, ma solo che la intersechi .
Ricapitolando, ecco i 5 casi ottenuti con l'ingrandimento del cerchio rosso
devo leggere attentamente i tuoi due ultimi commenti. Però nel frattempo ho fatto questa figura che mi dà 13 combinazioni. Al momento non ne vedo altre.
e questa?
Solo un'idea: se associamo un cerchio ad uno dei tre colori fondamentali p.e. Blu , Verde , Rosso
osserviamo che una sovrapposizione di due cerchi genera un colore secondario e una sovrapposizione di tre cerchi genera il bianco ( o nero).
Stante i vincoli possono prodursi solo le combinazioni
3P ,
1P1S, 2P1S, 3P1S,
1P2S, 2P2S,3P2s,
2P3S, 3P3S
che fanno 9 combinazioni.
Di queste solo 7 si combinano anche col nero ( o bianco) , per cui sembrerebbe , dico sembrerebbe, che le combinazioni totali siano 9+7=16 .
E' solo un'ipotesi
E bravo Leandro!
Per Mau (e non solo):
io ho seguito un metodo particolare che ha risolto il problema...
Ho disegnato tutte le configurazioni ottenibili con tre cerchi uguali, poi tutte quelle con due uguali e uno più piccolo, poi con due più piccoli e infine con tre grandezze diverse. Devo dire che non ho rischiato sovrapposizioni o mancanze...
Insomma, quante e quali sono????
E poi passiamo a 4 cerchi...
Cercando di dare una sistematicità alla ricerca ho provato ha classificare le relazioni tra cerchi in questo modo:
Intersecano (X), Esterni (E), Include(+), Incluso (-).
Poi ho assegnato queste relazioni alle combinazioni di cerchi C1-C2, C1-C3 e C2-C3 limitandomi alle combinazioni dei segni con ripetizione.
Di queste relazioni, alcune sono equivalenti. Credo perché nelle permutazioni delle relazioni "include" può diventare "incluso": es. C1 include C2, permutando i cerchi C2 incluso in C1.
Altre relazioni non sono logiche. Es. --E: C1 incluso in C2, C1 incluso in C3, C2 non può essere esterno a C3 poiché hanno in comune C1.
Infine c'è il caso delle 3 intersezioni che esplode in 6 sottocasi. Credo siano classificabili per la posizione del terzo cerchio rispetto alla intersezione dei primi 2.
Alla fine mi vengono questi 16 casi.
Invece io ho utilizzato il criterio di classificazione di Leandro e ho anche aggiunto alle 13 configurazioni che avevo trovato quella suggerita da lui.
Con i tre colori + il nero ho disegnato questa figura molto Kandiskyana in cui ci sono dei vuoti che non sono riuscito a colmare.
Delle possibili 18 configurazioni due erano state già escluse da Leandro che ipotizza l'esistenza di 16 configurazioni possibili.
Al momento due di queste 16 non le ho trovate, ma non è la prima volta che succede nella storia della umanità...
Nel 1871 Mendeleev e Meyer costruirono una tavola degli elementi formata da otto colonne, nelle quali erano raggruppati gli elementi con proprietà simili; per fare ciò, si dovettero lasciare degli spazi vuoti, affermando che dovevano esistere elementi non ancora scoperti.
Domani proverò (forse) a seguire il metodo suggerito da Vincenzo per generare tutto e subito. Dico forse perché con tutti questi cerchi comincia a girarmi la testa (e non solo)
Vedo che nel commento la figura è piuttosto sfocata. Nella libreria delle immagini è definita meglio. Comunque ingrandendo lo schermo e con un po' di buona volontà credo si riesca a leggerla.
Tra le ultime configurazioni di Fabrizio ho trovato le due che mi mancavano (quasi certamente le avevo generate e poi scartate ritenendole duplicazioni). A questo punto le ho classificate secondo il criterio di Leandro e le ho aggiunte alla mappa generale per vedere se andavano ad inserirsi proprio nei buchi.
Ebbene, è andata diversamente. Le due configurazioni vanno ad aggiungersi a quelle già presenti rispettivamente con le classificazioni N+ 3P2S e N+ 2P3S mentre i buchi restano vuoti.
In effetti la N + 3P sarebbe possibile solo sovrapponendo 3 cerchi uguali ma questo infrangerebbe la regola per la quale si possono avere solo 2 punti di contatto tra due cerchi.
La configurazione 1P 1S implica la presenza di solo 2 cerchi (uno contenuto nell'altro) mentre ne abbiamo 3.
La 2P 3S richiederebbe di spezzare un cerchio in due parti per non generare una triplice sovrapposizione.
La N+ 3P 1S infine non si può ottenere se non deformando un cerchio, quindi è illogica.
Però c'è qualcosa che non mi torna ancora...
Avevamo ragionato un paio di giorno fa sulla equivalenza di 2 configurazioni e alla fine sembrava che fossero la stessa cosa. Ora le ritrovo anche tra le 16 di Fabrizio come casi distinti.
Sono esattamente queste due...
Credo abbiate ragione. Non sono distinte. Si ottengono permutando il verde con il blu.
Io ho dato un'indicazione... adesso mettetevi d'accordo sul numero finale :roll
un bel disegnino con un numero accanto...
Ho rivisto i casi. Delle 7 menzionate , solo 5 si combinano ANCHE col nero e solo 2 SOLO col nero , totale = 14
Applicando le tue indicazioni ottengo questa collezione di 14 casi che ritengo privi di duplicazioni.
Ci sono altre configurazioni che ho scartato perché mi sembrano duplicati.
Perfetto Mau! Esattamente la figura che avevo preparato come soluzione... La configurazione meno ovvia è senz'altro quella individuata da Leandro, che mi sembra fosse sempre stata trascurata...
Oggi pubblico la prima parte della soluzione, ossia quella relativa ai tre cerchi... In attesa, sempre, delle ... Olimpiadi!
L'integrazione di Leandro, con quella particolare configurazione, è stata davvero provvidenziale.
A me era sempre sfuggita.
Tra le configurazioni che avevo elencato ci sarebbe anche questa.
E' da considerare equivalente a qualche altra configurazione presente nell'ultima lista di Maurizio?
Scusate, mi rispondo da solo. E' equivalente alla 4B.
Ciao Fabrizio, ruotando la tua figura di 90° a sinistra mi sembra corrisponda alla configurazione 4b.
Grazie comunque anche a te per avere segnalato, come Leandro, l'altra configurazione che mi era sfuggita.
Quasi contemporaneamente ( ho perso un minuto per i ringraziamenti, ma non me ne dolgo)