32. Con gli asintoti concludiamo lo studio di una funzione **
Concludiamo (almeno momentaneamente) lo studio delle funzioni con l'introduzione degli asintoti (orizzontali, verticali e obliqui). Vi lascio anche un paio di esercizi da svolgere...
Abbiamo studiato le caratteristiche più evidenti di una funzione, anche se ci sarebbero casi particolari ancora più complessi legati a funzioni decisamente più strane di un polinomio qualsiasi.
Tuttavia, vogliamo spingerci oltre e introdurre il concetto di integrale, gioia e dolore di molti appassionati. In qualche modo potremmo dire che esso non è altro che l’inverso della derivata, ma la sua importanza è tale che è estremamente importante valutare il suo significato sia attraverso una visione geometrica che analitica. Non chiedetemi, però, di partire in quarta… prima degli integrali è molto utile descrivere lo sviluppo in serie, ossia un metodo che ci permetta di approssimare una qualsiasi funzione attraverso una serie di termini in cui il successivo è sempre più piccolo del precedente. Un gioco estremamente utile per non rimanere bloccati da equazioni irrisolvibili o quasi.
Prima ancora, però, lasciatemi concludere con gli asintoti di una funzione. Concetto già incontrato che, però, ci permette di fare un piccolo ripasso di quanto svolto finora e ci riporta al nostro vecchio amico “infinito”. La Fig. 1 ci mostra i tre tipi di asintoto con cui avremo a che fare.
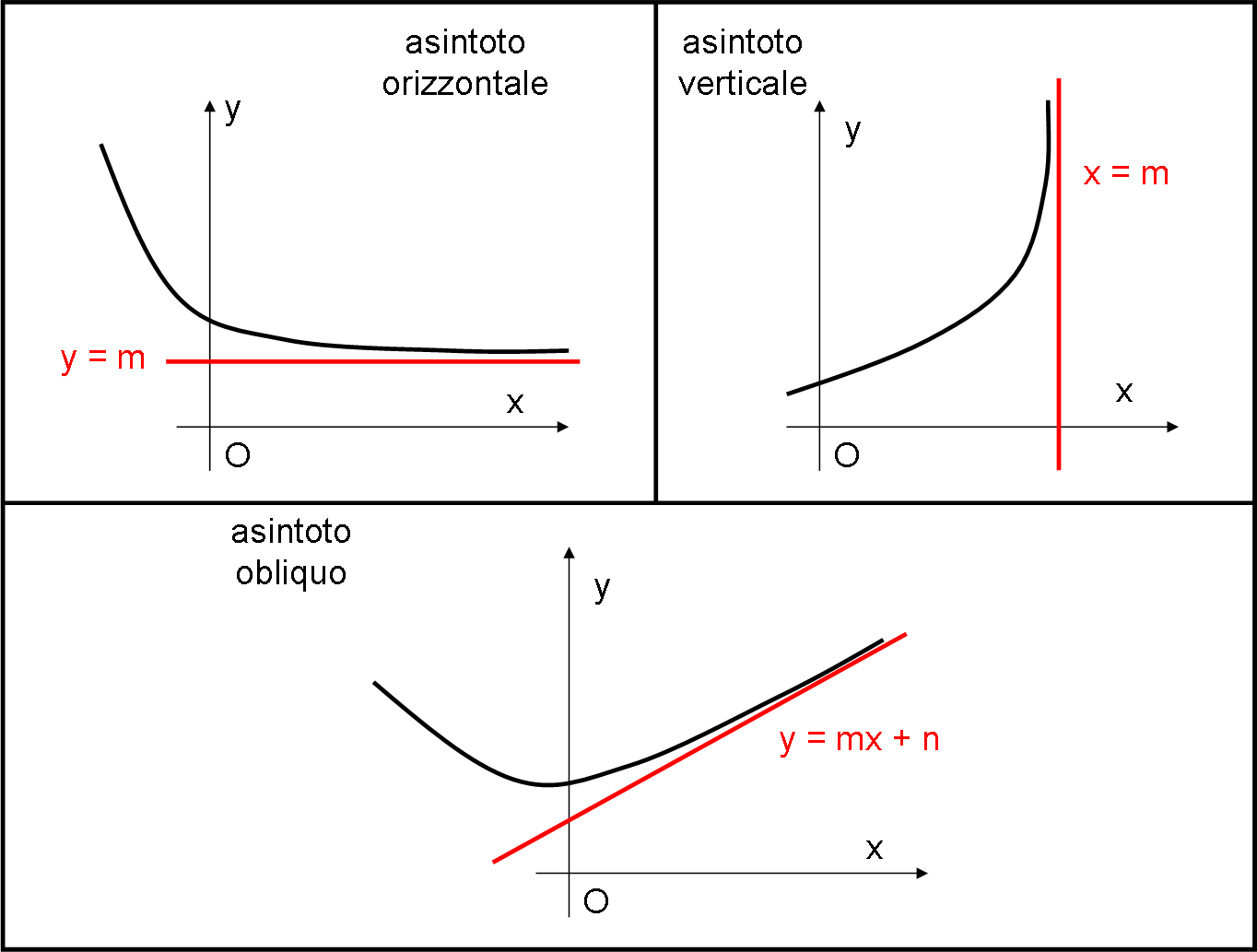
Asintoto orizzontale
Ricordiamo, innanzitutto, cosa significa asintoto. Dal greco, si ha una definizione molto chiara: “qualcosa che non si riesce mai a toccare”. Nel nostro caso, l’asintoto è una retta a cui la funzione si avvicina sempre più ma che riuscirà a toccare solo all’infinito. Vi appare subito chiaro un'altra definizione più geometrica… L’asintoto è la tangente nel punto all’infinito della nostra funzione. Ovviamente, non è detto che esista, in quanto spesso e volentieri sappiamo che al tendere di x all’infinito anche y tende a infinito e non lo fa sempre avvicinandosi a una retta. Ma, quando succede, siamo alla presenza di un asintoto.
Un caso banale e comune è l’asintoto orizzontale. In poche parole, esso si ha quando facendo tendere x a infinito, la y tende a un valore costante, ossia a una retta del tipo y = cost. L’asintoto è, appunto, orizzontale dato che la retta è una retta orizzontale.
Un esempio lampante l’abbiamo nel caso dell’iperbole equilatera, di equazione:
y = 1/x
Quando x tende a infinito, y tende a zero. L’asse delle x (y = 0) è l’asintoto orizzontale della nostra funzione.
Se scrivessimo:
y = 1/x + m
Otterremmo che l’asintoto orizzontale diventebbe y = m (il limite di una costante è sempre la costante).
La definizione matematica dell’asintoto orizzontale si scrive, perciò, facilmente come:
lim x→∞ f(x) = m = cost.
E ci permette di concludere che si ha un asintoto orizzontale quando la funzione tende a un numero finito per la x che tende a infinito (o a meno infinito, ovviamente).
Facciamo un esempio un po’ più complicato:
y = 2x/(x-5)
Esiste un asintoto orizzontale? Eseguiamo il limite per x che tende a ∞.
lim x→∞ (2x/(x-5))
Abbiamo immediatamente una forma indeterminata del tipo ∞/∞ che si risolve immediatamente dato che numeratore e denominatore hanno lo stesso grado e, quindi, il limite non è altro che il rapporto tra i termini del grado massimo, ossia:
lim x→∞ (2x/(x-5)) = 2/1 = 2
L’asintoto orizzontale è quindi dato dalla retta y = 2.
La funzione ammette lo stesso asintoto anche per x che tende a meno infinito. Infatti vale sempre:
lim x→- ∞ (2x/(x-5)) = 2/1 = 2
Asintoto verticale
La sua definizione è esattamente l’opposto di quella precedente. Esiste un valore di x tale che la y tenda a infinito proprio per quel valore di x? In altre parole, la y tende a infinito per un valore costante di x. E’ come se ribaltassimo la figura, trasformando x con y. La definizione è ovvia:
lim x→m f(x) = ∞
Ovviamente, il nome “verticale” dipende dal fatto che la funzione si avvicina sempre più a una retta verticale, di equazione x = m.
Come si possono determinare? Molto facilmente… Dato che la y deve andare a infinito, gli asintoti saranno dati dalle x che annullano il denominatore (ma non anche il numeratore…). Solo in queste condizioni la y va a infinito!
Riprendiamo l’esempio dell’iperbole:
y = 1/x
L’unico valore per cui la y tende a infinito è dato da x = 0, ossia:
lim x→0 f(x) = ∞
L’asse delle y (x = 0) è quindi asintoto verticale della funzione y = 1/x
Niente cambia se la funzione diventa y = 1/x + m, dato che aggiungere m a infinito dà sempre infinito. Diversa è la situazione se.
y = 1/(x – 1)
In questo caso la funzione va a infinito per x – 1 = 0 ossia per x = 1. L’asintoto verticale è dato da x = 1.
Stiamo molto attenti a far tendere a m la x sia da sinistra che da destra, dato che il segno di infinito può cambiare completamente.
Nel caso y = 1/(x-1) abbiamo risultati opposti. Per x che tende a 1 da sinistra (ossia provenendo da numeri minori di 1) il denominatore è un numero sempre più piccolo, ma negativo e tale è quindi anche l’infinito a cui tende y. Per x che tende a 1 da destra (numeri più grandi di 1) l’infinito è sempre positivo e quindi la funzione tende a infinito verso l’alto.
La funzione y = 1/(x-1) ha quindi un solo asintoto verticale (x = 1), ma a destra di questa retta la funzione tende a + ∞, mentre a sinistra la funzione tende a - ∞. Un gran bel salto!
Ben diversa sarebbe la soluzione per y = 1/(x -1)2.
In questo caso la differenza (x – 1) può diventare maggiore o minore di zero provenendo da sinistra o da destra, ma il suo quadrato è sempre positivo e quindi, sia prima che dopo l’asintoto, la funzione tende ad andare verso l’alto, ossia verso + ∞.
Divertitevi a disegnare qualche semplice funzione, inventata da voi, che abbia asintoti verticali e/o orizzontali.
Asintoti obliqui
Più complicata è la determinazione degli asintoti obliqui. Essi sono rette qualsiasi verso cui tende la nostra funzione mentre la x sta andando all’infinito. Ne segue, in questo caso, che al tendere della x all’infinito, la y deve comunque tendere a infinito (così come fa anche una retta). Deve valere, perciò:
lim x→∞ f(x) = ∞
Beh… questa sola formula ci direbbe ben poco, dato che molte funzioni la soddisfano, pur senza avere asintoti obliqui (ad esempio la parabola). E’ necessario introdurre ulteriori informazioni.
La retta asintoto, se esiste, ha comunque un’equazione del tipo:
y = mx + n
Dato che al tendere di x all’infinito, la funzione f(x) deve “toccare” questa retta, deve valere la relazione:
lim x→∞ (f(x) – (mx + n)) = 0 …. (1)
Utilizzando quanto sappiamo delle operazioni sui limiti, possiamo dire che il limite di un prodotto è uguale al prodotto dei limiti e viceversa, ossia:
lim x→∞ (f(x) · g(x)) = lim x→∞ f(x) · lim x→∞ g(x)
Sappiamo però anche che 0 · 0 = 0
Dato che la (1) vale zero, posso moltiplicarla tranquillamente per qualcosa che vale zero: il prodotto continuerà a valere zero. In particolare posso usare l’espressione:
lim x→∞ (1/x)
Questo limite vale sicuramente zero (1/∞ = 0)
Posso allora scrivere tranquillamente:
lim x→∞ (f(x) – (mx + n)) · lim x→∞ (1/x) = 0
ma anche (il prodotto dei limiti è uguale al limite del prodotto):
lim x→∞ ((f(x) – (mx + n)) · (1/x)) = lim x→∞ ((f(x) – mx - n)/x) = 0
lim x→∞ f(x)/x - lim x→∞ m - lim x→∞ n/x = 0
lim x→∞ f(x)/x – m – 0 = 0
E, infine:
lim x→∞ f(x)/x = m …. (2)
Il coefficiente angolare della retta asintoto è dato dal limite tra la funzione e l’ascissa x.
In modo molto più semplice, possiamo scrivere di nuovo la (1) e ottenere:
lim x→∞ (f(x) – (mx + n)) = lim x→∞ f(x) - lim x→∞ mx - lim x→∞ n = 0
lim x→∞ (f(x) – mx) – n = 0
E, infine:
lim x→∞ ( f(x) – mx) = n …. (3)
La retta asintoto è completamente determinata!
Ne segue che per determinare se una funzione ha un asintoto obliquo basta calcolare i due limiti dati dalla (2) e dalla (3). Se essi danno un risultato finito, la risposta è SI e la (2) e la (3) ne forniscono i coefficienti atti a definirla.
Facciamo un esempio semplice semplice:
y = (2x2 - 1)/x
Vale sicuramente
lim x→∞ (2x2 - 1)/x = ∞
Proviamo a calcolare m
m = lim x→∞ (2x2 - 1)/x2 = 2
Il numeratore e il denominatore hanno lo stesso grado e il risultato è il rapporto tra i coefficienti dei termini di grado superiore.
Proviamo a calcolare n
n = lim x→∞ ((2x2 - 1)/x – 2x) = lim x→∞ (2x2 – 1 – 2x2)/x = lim x→∞ (– 1/x) = 0
Perfetto!
Esiste l’asintoto obliquo e ha equazione
y = 2x
Lascio a voi il “divertimento” di disegnare questa bella funzione…
Breve discussione sull’esistenza degli asintoti
In realtà è abbastanza semplice capire subito, guardando la funzione, se essa ha asintoti orizzontali, obliqui o ne è priva: basta confrontare l’ordine di infinito del numeratore e del denominatore.
Infatti, se essi sono dello stesso ordine il limite della funzione sarà uguale al rapporto tra i due coefficienti dei termini di grado superiore. Ossia avremo un asintoto orizzontale, del tipo y = m.
Se, invece, il denominatore ha ordine superiore, il limite dà come risultato zero e quindi l’asintoto orizzontale è del tipo y = 0.
Esiste un asintoto obliquo se il numeratore è un infinito di un solo ordine superiore al denominatore. Infatti, quando si moltiplica il denominatore per x l’ordine si pareggia e il valore di m sarà un numero finito.
Infine, se il numeratore ha un ordine superiore di due o tre o più di quello del denominatore, m non può che essere infinito e non vi può essere asintoto obliquo.
In realtà, a mano a mano che il numeratore sale di grado potremmo dire che la funzione si avvicina all’infinito a una parabola, un cubica, ecc. Quest’ultima caratteristica sarà molto utile per capire il processo di approssimazione dello sviluppo in serie e il significato geometrico delle derivate successive
L’esistenza di un asintoto verticale è immediatamente evidenziata se esiste un valore finito di x che annulla solo il denominatore.
Concludiamo qui la trattazione delle funzioni, rimandando a tempi futuri lo studio di funzioni particolari che non siano solo composte da polinomi. E’ più urgente passare alle serie e, infine, agli integrali.
Lascio comunque un paio di esercizi per i più volenterosi.
Eseguire lo studio completo delle due funzioni che seguono
1) y = - (x2 + 2x)/(1 – x)
2) y = x/(x2 – 1)
Chi vuole fare un saltino in più, può anche provare con questa:
3) y = (1 – x3)1/2
Buon divertimento…
QUI il capitolo precedente
QUI il capitolo successivo
QUI l'intero corso di matematica






7 commenti
Caro Enzo, ho lavorato parecchio per trasformare in grafici tutte le funzioni che hai indicato nel tuo articolo.
per trasformare in grafici tutte le funzioni che hai indicato nel tuo articolo.
Per evitare limiti di immagini imposti automaticamente dal blog, dividerò il post in quattro parti...
Prima di iniziare devo dire che lo studio di alcuni funzioni è stato anche un ottimo esercizio per calcolare le derivate.
In ogni figura ho indicato oltre alla funzione iniziale anche la derivata prima e la derivata seconda, così è piuttosto semplice vedere se hanno qualche possibilità di annullarsi.... ossia se possono esistere: Flessi orizzontali, Flessi obliqui, Minimi e Massimi.
Parto dalla funzione più semplice:
y= 1/x
Una bella iperbole equilatera in cui gli asintoti (uno verticale ed uno orizzontale) coincidono con gli assi cartesiani y ed x.
Come al solito invece della curva ho indicato una serie di punti in blu chiaro:
http://www.astrobin.com/full/215950/E/
Guardando le due derivate è evidente che solo quando x è uguale a infinito, le derivate si annullano, quindi niente Minimi, Massimi, o flessi.
Nella prossima figura ho confrontato due varianti della funzione di prima, ossia:
y= 1/(x-1) e y = 1/(x-1)²
http://www.astrobin.com/full/215950/F/
La prima curva è la stessa iperbole equilatera di prima solo che è spostata di un'unità verso destra.
La seconda dato che (x-1) è elevato al quadrato non può che restituire solo valori positivi di y, ed infatti rispetto alla curva della figura al suo fianco, la parte negativa presente nella funzione precedente è ribaltata verticalmente
Gli Asintoti sono rimasti gli stessi e le derivate si annullano solo con x uguale a infinito.
L'ultima figura di questa prima parte mostra il grafico della funzione: 2x/(x-5)
http://www.astrobin.com/full/215950/G/
L'iperbole ha cambiato forma (i due rami dell'iperbole sono più aperti) e i due asintoti orizzontale e verticale hanno ascisse e ordinate diverse rispetto a prima.
Il valore dell'Asintoto verticale è facilmente ricavabile, poiché la funzione tende ad infinito quando il denominatore tende a zero e dato che il denominatore è (x-5), quando x vale +5 il denominatore vale zero!
Come al solito le derivate prima e seconda non possano annullarsi.
Infatti in un rapporto, affinché questo restituisca come risultato zero, il numeratore deve essere uguale a zero, per cui basta vedere se esiste un valore di x che consente al numeratore di andare a zero (esiste però un eccezione a questa osservazione, ossia che se lo stesso valore della x annulla sia il numeratore, sia il denominatore, si ha a che fare con una forma indeterminata 0/0).
Questa prima parte termina con la segnalazione di un piccolo refuso:
quando introduci gli Asintoti Obliqui, dopo la formula lim x→∞ f(x) = ∞ dici:” questa sola formula ci direbbe ben poco, dato che molte funzioni la soddisfano, pur senza avere flessi obliqui (ad esempio la parabola)”...... se non ho capito male più che di flessi obliqui la frase si riferisce agli Asintoti Obliqui...
La prossima figura riguarda la curva che avevi chiesto di descrivere, ossia quella che rappresenta la funzione: y = (2x² -1)/x
http://www.astrobin.com/full/215950/H/
Questa volta i due asintoti (Verticale e Obliquo) dei rami dell'iperbole non sono più perpendicolari fra loro...
Anche in questo caso le derivate non si annullano.....
La derivata prima può trarre in inganno: y' = (2x² +1)/x²
il numeratore non può annullarsi, poiché ci vorrebbe un 1 da sottrarre ad 1, mentre la x è elevata al quadrato e restituisce solo risultati positivi.
A questo punto non resta che passare agli esercizi, con la precisazione che ho riportato solo i tratti salienti dei vari passaggi matematici (il metodo usato) senza riportare tutti i singoli passaggi …..
Comunque nei vari passaggi è necessario prestare un attenzione maniacale ai segni, che vanno rigidamente rispettati....
Parto dalla prima funzione.
y = - (x² + 2x)/(1 – x)
non ci sono asintoti orizzontali, poiché la x del denominatore ha grado inferiore rispetto alla x del numeratore e quindi non è possibile rispettare la condizione:
lim x→∞ ƒ(x) = m = costante
Controllo se ci sono asintoti verticali, in tal caso il denominatore si annulla (è uguale a zero) quando x tende a un numero finito, ossia deve essere soddisfatta la condizione:
lim x→m f (x) = ∞
lim x→m - (x² + 2x)/(1 – x)
per essere uguale a infinito il denominatore deve valere 0, ossia: (1 – x) = 0
Tale condizione è soddisfatta solo se x = 1
lim x→m - (1² + 2 (1)) /(1 – (1)) = - ∞
Attenzione però che se arrivo ad 1 da sinistra (valori di x inferiori ad 1) il denominatore è positivo, ma il numeratore è negativo, per cui si ha -∞.
Al contrario se la curva arriva ad 1 da destra (valori di x maggiori di 1) il denominatore diventa negativo, come il numeratore, per cui si ha + ∞
La funzione quindi ha un asintoto verticale che attraversa l'asse delle ascisse quando x=1, la curva della funzione perciò tende a - ∞ se si avvicina all'asintoto da sinistra (valori di x minori di 1), mentre tende a + ∞ se si avvicina all'asintoto da destra (valori di x maggiori di 1).
La retta che rappresenta l'asintoto verticale, parallela all'asse y, è data da x = 1
Per vedere se esistono anche degli asintoti obliqui, il numeratore deve essere di un solo grado superiore rispetto al denominatore...
La funzione y = - (x² + 2x)/(1 – x) sembra possedere questa caratteristica (x² sopra e x sotto).
Innanzitutto provo a trovare il coefficiente angolare della retta che rappresenta l'asintoto obliquo:
m =lim x→∞ f (x)/x
m = lim x→∞ -(x² + 2x)/(1 – x) x
m = lim x→∞ -(x² + 2x)/(x – x²)
sia al denominatore che al numeratore ho una x di secondo grado, entrambe con segno negativo, quindi eseguo il rapporto tra i due coefficienti (ossia -1 e -1):
m = lim x→∞ -(x² + 2x)/(x – x²) = -1/-1 = +1
Una volta trovato il coefficiente angolare m, non resta che trovare quello di n:
n= lim x→∞ (f (x) – mx)
n= lim x→∞ (-(x² + 2x)/(1 – x) – x (1))
n= lim x→∞ -3x/(1 – x) le x sono dello stesso grado, quindi:
n= lim x→∞ -3x/(1 – x) = -3/-1 = +3
La retta che rappresenta l'asintoto obliquo ha coefficiente angolare uguale a +1 e attraversa l'asse delle y a +3 (n), per cui la sua funzione è: y = x +3
Per vedere se esistono Minimi, Massimi o flessi, calcolo la derivata prima della funzione:
y = - (x² + 2x)/(1 – x)
Bisogna trovare la derivata di un rapporto tra funzioni, ossia:
y = f(x)/g (x)
y’ = (f'(x) g(x) - f(x) g'(x))/g(x)²
dato che la funzione iniziale è composta da:
f(x) = (- x² – 2x)
f'(x) = (-2x -2)
g (x) = (1 – x)
g' (x) = (-1)
y' = (-2x -2) (1 – x) - (- x² -2x)(-1)/(1 -x)²
y' = 1 - 3/(1 – x)²
annullo la derivata prima
0 = 1 - 3/(1 – x)²
0 = x² -2x – 2
Si tratta di un'equazione completa di secondo grado, ax² -bx – c =0, dove
a=1; b=-2 c=-2, le cui due soluzioni sono:
x1,2 = (-b +/-√(b² – 4ac))/2a
x1,2 = (-(-2) +/-√((-2)²– 4 (1) (-2))/2 (1)
x1,2 = +2 +/-√12/2
x1 = +2 -√12/2 = -0,73
x2 = +2 +√12/2 = +2,73
A tali ascisse corrispondono le ordinate (basta sostituire x nella funzione iniziale):
y = - (x² + 2x)/(1 – x)
y1 = - ((-0,73)² + 2(-0,73))/(1 – (-0,73)) = +0,536
y2 = - ((+2,73)² + 2 (2,73))/(1 – 2,73) = + 7,46
A questo punto per vedere di quali punti si tratta e se esiste anche un flesso obliquo, calcolo la derivata seconda:
y' = 1 - 3/(1 – x)² = 1 - 3 (1 – x)^-²
Per calcolare la derivata bisogna tener conto che si ha a che fare con una costante moltiplicata per una funzione di una funzione -3 (1 – x)^-²
y = f (g(x))
y’ = f ’(g(x)) g’(x)
Nella nostra funzione:
f (g(x)) = -3 (1 – x)^-² …...............f'(g(x)) = 6 (1 – x)^-³
g(x) =-x..........................................g'(x) = -1
y'' = 6 (1 – x)^-³ (-1) = - 6/(1 – x)³
A questo punto è facile determinare cosa rappresentano i punti che annullano la derivata prima:
x1 = -0,73
y'' = - 6/(1 – (-0,73))³ = -6/(1 +0,73))³ = -1,16
dato che il numeratore è negativo e il denominatore positivo, la derivata seconda è negativa, quindi il punto con ascissa x1 rappresenta un Massimo (-0,73; 0,536)
x2 = +2,73
y'' = - 6/(1 – 2,73)³ = +1,16
dato che numeratore è denominatore sono entrambi negativi, la derivata seconda è positiva, per cui il punto con ascissa x2 rappresenta un Minimo (2,73; 7,46).
Non ci sono flessi obliqui, poiché la derivata seconda si annulla solo se x = ∞.
y'' = - 6/(1 – x)³
Prima di disegnare la funzione calcolo i punti in cui la curva taglia l'asse della ascisse, (y=0):
0 = (- x² -2x)/(1 – x)
0 = - x (x + 2)
Ci sono quindi due soluzioni che annullano la funzione iniziale:
a) x = 0
Punto A (0;0), ossia la curva passa per l'origine degli assi.
b) x+ 2 = 0
x= -2
la curva taglia l'asse x anche nel punto Punto B (-2;0).
Dopo tanti calcoli, ecco il risultato

http://www.astrobin.com/full/215950/I/
La seconda funzione da analizzare é: y = x/(x² – 1)
Non esistono Asintoti obliqui dato che il numeratore è di grado inferiore rispetto al denominatore
Dovrebbe esistere invece un asintoto orizzontale, del tipo y=0, dato che il denominatore ha ordine superiore.
lim x→∞ ƒ(x) = lim x→∞ x/(x² – 1) = ∞/∞² =1/∞ = 0 (m costante =0)
In questo caso l'asintoto orizzontale è rappresentato dall'asse x delle ascisse:
Dovrebbe esistere anche un asintoto verticale, dato che il denominatore si annulla con un valore finito di x:
lim x→m f (x) = ∞
lim x→m x/(x² – 1) = ∞
per essere uguale a infinito il denominatore deve valere 0, ossia:
x² – 1 =0
x² = 1
x = +/- √1
x1 = -1
x2 = +1
Quindi oltre all'asintoto orizzontale, ci sono anche due asintoti verticali (rette parallele all'asse y) che tagliano l'asse x nei punti x=-1 e x=1.
Tra l'altro per ognuno di questi due asintoti bisogna vedere da dove si arriva a +1 e -1, poiché se per esempio all'asintoto x1 = -1 ci si avvicina da sinistra (x minore di -1)
y = x/(x² – 1) il numeratore ha segno negativo ma il denominatore positivo poiché x² restituisce sempre un numero positivo che se è è maggiore di 1 rende il denominatore positivo per cui la y tende a -∞, mentre se si arriva da destra (x maggiori di -1, come -0,9) il numeratore ha segno negativo, ma ciò accade anche al denominatore poiché il risultato di x² è minore di 1 e quindi il denominatore assume segno negativo come il numeratore, per cui y tende a +∞.
Lo stesso accade anche per il secondo asintoto verticale, x=1, poiché mentre il numeratore rimane positivo, dato che la x al denominatore è elevata al quadrato e restituisce sempre un risultato positivo se x è maggiore o minore di 1 cambia il segno del denominatore.
Quindi la curva tende a -∞, prima di arrivare all'asintoto verticale x= -1, dopodichè ricompare da +∞ dopo il primo asintoto e di nuovo tende a -∞ prima di raggiungere il secondo asintoto verticale, per poi ricomparire da +∞ dopo aver superato x=1, ossia il secondo asintoto verticale.
A questo punto, calcolo la derivata prima:
y = x/(x² – 1)
Per ricavare la derivata è necessario trovare la derivata di un rapporto tra funzioni, ossia:
y = f(x)/g (x)
y’ = (f'(x) g(x) - f(x) g'(x))/g(x)²
Nella nostra funzione:
y = x/(x² – 1)
f(x) = x...........................f'(x) = 1
g (x) = (x² – 1)...............g' (x) = 2x
y’ = ((1) (x² – 1) - (x) (2x))/(x² – 1)²
y’ = - (x² + 1)/(x² – 1)²
Affinché la derivata prima possa annullarsi, il numeratore dovrebbe annullarsi, ma ciò è impossibile poiché qualunque numero elevato al quadrato fornisce un risultato positivo, che si somma a +1.....
Quindi la derivata prima non può annullarsi e non esistono né Minimi, né Massimi, né Flessi orizzontali.
A questo punto non resta che vedere se esistono dei Flessi obliqui, ossia se la derivata seconda si può annullare:
y’ = - (x² + 1)/(x² – 1)²
y’ = (-x² - 1) (x² – 1)^-²
Si tratta di un prodotto tra funzioni, e la seconda funzione è una funzione di una funzione:
f (x) = (-x² - 1)
f' (x) = -2x
g(x) = (x² – 1)^-² = 1/(x² – 1)²
f'(gx1) (g'x1)
f'(gx1) = -2 (x² – 1)^-3
g'x1 = 2x
g'(x) = 2x -2 (x² – 1)^-3 = - 4x(x² – 1)^-3 =- 4x/(x² – 1)3
y = f (x) g(x)
y' = f'(x) g (x) + g'(x) f(x)
y'' = (-2x) 1/(x² – 1)² + - 4x (-x² – 1)/(x² – 1)³
y'' = 2x³ +6x /(x² – 1)³
Annullo la derivata seconda:
0 = 2x³ +6x /(x² – 1)³
2x (x² +3) =0
Ci sono più soluzioni:
a) x=0
b) x² +3 =0
x² =-3
x =+/-√-3
L'unica soluzione reale è x=0, poiché la radice quadrata numero negativo non fornisce numeri reali.
Dato che la funzione iniziale è:
y = x/(x² – 1) = 0/(0² – 1) = 0
Se x=0 anche y=0, quindi il punto di Flesso Obliquo F(0;0) è l'origine degli assi.
Sostituendo l'ascissa del punto di Flesso (x=0) nella derivata prima si ottiene il coefficiente angolare della retta tangente il punto di flesso obliquo:
m= y’ = - (x² + 1)/(x² – 1)² = - (0² + 1)/(0² – 1)²
m = - 1/1 = -1
La retta tangente il flesso obliquo passa per l'origine degli assi F(0;0)
A questo punto basta guardare il comportamento della derivata seconda:
y'' = 2x³ + 6x /(x² – 1)³
Con valori di x di poco inferiori a 0 (negativi), la derivata seconda è positiva (sia numeratore che denominatore hanno segno meno), mentre con valori di x leggermente maggiori di zero (positivi) la derivata seconda è negativa, dato che il numeratore è positivo e il denominatore negativo.
Quindi la derivata seconda passa da positiva a negativa ed il Flesso Obliquo è discendente.
Infine vediamo se esistono punti che annullano la funzione di partenza:
y = x/(x² – 1)
0 = x/(x² – 1) solo con x=0 si annulla la funzione iniziale
La Figura mostra questa strana curva che salta da +∞ a -∞ e viceversa.
http://www.astrobin.com/full/215950/J/
Manca solo l'ultima funzione: y = √(1 – x³)
Innanzitutto, non possono esistere soluzioni reali con una radice quadrata di un numero negativo.
Quindi x³ deve necessariamente essere inferiore a 1 (o negativo).
Ossia la funzione ammette solo valori di x negativi e valori positivi compresi tra 0 ed +1 e la y è sempre positiva.
Non dovrebbero esserci Asintoti Orizzontali, dato che se x tende a ∞ o meglio a - ∞, y tende a +∞ , ossia se x tende a +/-∞ la funzione non tende ad un numero finito.
lim x→-∞ √(1 – x³) = √(1 – (-∞³)) = √(1 + ∞) = + ∞
Non ci sono nemmeno Asintoti verticali, poiché se x tende ad un numero finito, la funzione può andare a 0 (x =1), ma non a infinito:
lim x→m f (x) = ∞
lim x→m f √(1 – x³) = ∞
Provo a vedere se esistono Asintoti Obliqui.
Usando la formula per determinare il coefficiente angolare di un Asintoto Obliquo, si ottiene (uso il limite di -∞, per non incorrere in radici quadrate negative) :
m= lim x→-∞ f (x)/x
m= lim x→-∞ √(1 – x³)/x
elevo entrambi al quadrato
m²= lim x→-∞ √(1 – x³)²/x² =(1 – x³)/x² = ∞³/ -∞² = ∞
m = √∞ = ∞
Quindi non ci sono nemmeno asintoti obliqui, dato che non esiste un coefficiente angolare m di valore finito.
A questo punto calcolo la derivata prima per vedere se ci sono Massimi, Minimi o Flessi Orizzontali.
y= √(1 – x³) = (1 – x³)^1/2
è una funzione di funzione:
y' = f'(gx) g'(x) =
y'= -3x²/2√(1 – x³)
La derivata prima si annulla se il numeratore va a zero ed il denominatore no:
0 = -3x²/2√(1 – x³)
0 = -3x²
solo se x=0 si annulla la derivata prima
All'ascissa del punto che annulla la derivata prima (x=0) corrisponde l'ordinata:
y = √(1 – x³) = √(1 – 0³) = +1
Per vedere di quale punto si tratta, calcolo la derivata seconda:
y' = -3x²/2√(1 – x³)
Si tratta di una costante (3/2) moltiplicata per un rapporto tra funzioni, e la funzione al denominatore è una funzione di funzione:
y' = -3x²/2√(1 – x³) che riscrivo così:
y' = 3/2 -x²/√(1 – x³)
Prima calcolo la derivata del rapporto tra funzioni:
y = f(x)/g (x)
y’’ = (f'(x) g(x) - f(x) g'(x))/g(x)²
f (x) = -x²
f' (x) = -2x
g(x) = √(1 – x³) = (1 – x³)^1/2
g'(x) = 1/2 (1 – x³)^-1/2 (-3x²) = -3x²/2√(1 – x³)
y’ = ((-2x) √(1 – x³) - (-x²) (-3x²/2√(1 – x³) ) /(1 – x³)
y’ = (-2x 2√(1 – x³)√(1 – x³) - (-x²) (-3x²/√(1 – x³) (1 – x³)
y’ = (-4x (1 – x³) - 3x^4/2√(1 – x³) (1 – x³)
y’ = (-4x + 4x^4 - 3x^4/2√(1 – x³) (1 – x³)
y’ = (-4x + x^4)/ 2(1 – x³)^3/2
y’ = x (-4 + x³)/2 (1 – x³)^3/2
y’ = x (x³- 4)/ 2 (1 – x³)^3/2
Infine la moltiplico per la costante 3/2:
y'' = 3/2 x (x³- 4)/ 2 (1 – x³)^3/2
y'' = 3x (x³- 4)/ 4 (1 – x³)^3/2
Per annullarsi la derivata seconda deve annullarsi il numeratore:
0 = 3x (x³- 4)
0 = x (-12+ 21 x³)
ci sono due soluzioni:
a ) x = 0, per cui dato che l'ascissa x=0, annulla sia la derivata prima, sia la derivata seconda, si tratta sicuramente di un Flesso Orizzontale F (0; 1)
Per valori di x inferiori a 0, la derivata seconda è positiva, infatti:
y’’ = 3 (-1) ((-1)³- 4)/ 4 (1 – (-1)³)^3/2
y’’ = -3 (-5)/ 4 (1+1)^3/2
y’’ = +15/ +4 (2)^3/2
Per valori maggiori di x=0 diventa negativa:
y’’ = 3 (0,5) ((0,5)³- 4)/ 4 (1 – (0,5)³)^3/2
y’’ = -3 (0,125)/ 4 (1-0,125)^3/2
y’’ = -0,375/ +4 (0,875)^3/2
Quindi si tratta di un Flesso Orizzontale Discendente (la derivata seconda passa da valori positivi a valori negativi).
la seconda soluzione che annulla la derivata seconda è invece data da:
b)
(x³- 4) = 0
x³ = 4
x = (4)^1/3 = 1,58
Ma nella funzione in esame x non può superare valori maggiori di +1, per cui non ci sono altri punti che annullano la funzione iniziale e quindi non ci sono Flessi Obliqui.
D'altronde basta guardare la relazione
(x³- 4) = 0
La x deve essere positiva ed eguagliare 4, ma il massimo valore che può raggiungere la x è +1, il cui cubo è +1!
La Figura mostra questa strana curva, che si interrompe quando raggiunge l'asse x all'ascissa x=1 nel punto A (1;0), l'unico punto che annulla la funzione inziale:
0 = √(1 – x³)
0 = √(1 – (1)³) =√0 =0
http://www.astrobin.com/full/215950/K/
Una piccola domanda, sono corrette le soluzioni (soprattutto l'ultima derivata seconda, in cui ho separato la costante, calcolato la derivata del rapporto tra funzioni e poi l'ho moltiplicata per il risultato)?
Paolo
grande Paolo!!!!


sei diventato un vero mago. E grazie anche per il refuso... L'ultima non era semplice, soprattutto da accettare come andamento...
E sì, una costante moltiplicata per una funzione rimane tale e quale e si può estrarre come hai fatto tu.
Ma sei sicuro di non avere mai studiato le funzioni prima di questo circolo?
Caro Enzo, di quanto studiato a scuola all'ITIS, ricordo ben poco.... però posso assicurarti che non avevo mai studiato le funzioni in maniera così efficace e approfondita (è tutto merito dei tuoi articoli ).....
).....
Degli integrali ho solo un vaghissimo ricordo concettuale, ossia di una sommatoria di intervalli piccolissimi in un certo intervallo........ e leggendo i tuoi articolo mi sono fatto la vaga idea che una curva sia ricostruibile come una sommatoria di segmenti piccolissimi, o meglio di “punti” piccolissimi, come quelli il cui comportamento viene rappresentato dalle derivate.... se poi ricostruisco ("sommo") tutti questi punti ed il loro comportamento in un certo intervallo di x....
Come vedi ho solo delle vaghe idee, ma sono sicuro che con i prossimi articoli la nebbia comincerà a diradarsi aprendo la strada alla conoscenza degli integrali.
Paolo
caro Paolo, Ancora complimenti
Ancora complimenti 
se tutti gli studenti fossero come te...