Bravissimi, come sempre, Maurizio e Fabrizio per aver risolto il quiz che altro non era che l'applicazione "pratica" del teorema di Bottema, dovuto a Oene Bottema (Groningen, 1901–1992).

Il teorema parte da un triangolo qualsiasi ABC e considera i quadrati costruiti sopra due suoi lati, ad esempio AC e BC. I due quadrati hanno un punto in comune, ossia C. Tracciando il segmento che unisce tra loro i vertici dei quadrati opposti a C, il punto medio M è indipendente dalla posizione di C. In altre parole, mantenendo fisso il lato AB, qualsiasi triangolo abbia lui come lato determina uno e un solo punto M. La Fig. 1 illustra bene la situazione:

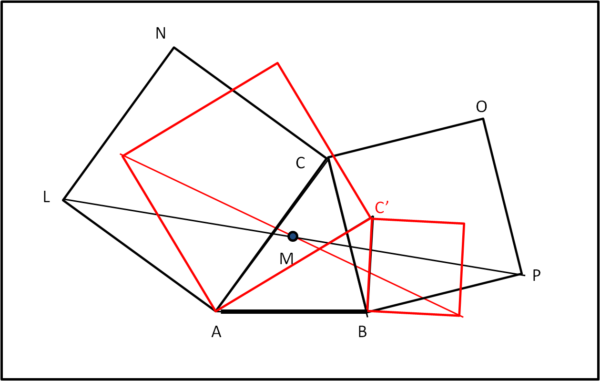
Costruendo i quadrati sul triangolo nero ABC o su qualsiasi altro triangolo rosso ABC', il punto M rimane sempre lo stesso.

Non ci resta che dimostrarlo...

Consideriamo la Fig. 2

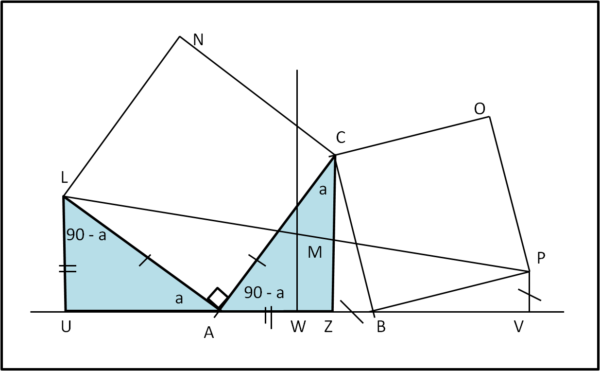
e tracciamo le perpendicolari LU, MW, BV e CZ ad AB.

MW è la linea mediana del trapezio LPVU, per cui si può scrivere:

MW = (LU + PV)/2

Consideriamo i due triangoli rettangoli azzurri. Essi sono congruenti, avendo i tre angoli  e l'ipotenusa uguali. Ne segue:

LU = AZ

In modo analogo si ottiene che:

PV = BZ

Le identità trovate ci permettono di scrivere:

MW = (LU + PV)/2 = (AZ + BZ)/2 = AB/2 = AW

Risultato del tutto indipendente dalla posizione di C.

Dobbiamo dire che, in realtà, la conoscenza di questo teorema permette proprio di sotterrare qualcosa senza lasciare traccia alcuna, con la sicurezza di trovare subito il punto misterioso. Basta, infatti, che vi siano due punti ben evidenti e non mobili (il fico e l'olmo) e poi qualsiasi punto C si scelga si arriva sempre a M.

La matematica e la geometria sanno essere magiche...