Prima di passare a capitoli più impegnativi, vediamo di riprodurre l'esempio del segnale "a scatto" del capitolo precedente attraverso una rappresentazione puramente grafica che permette la costruzione di sinusoidi estremamente complesse. Un piccolo "intervallo" in mezzo a un diluvio di formule...

Sappiamo che un moto armonico  può essere descritto come l'ordinata (o l'ascissa) di un punto che si muove di moto circolare uniforme. Vediamo subito a cosa mi riferisco con la Fig. 1.

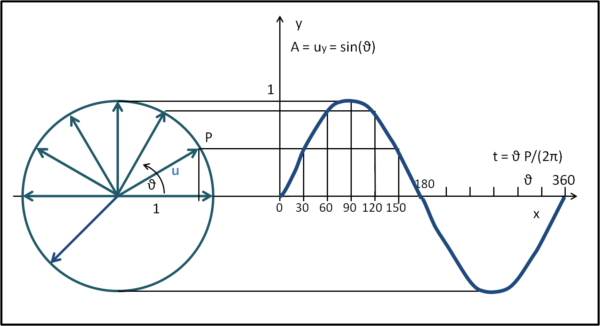
Consideriamo un vettore u di modulo unitario e lo facciamo girare con moto uniforme attorno a un punto fisso. La punta del vettore (P) descrive un cerchio di raggio unitario. Se, per ogni θ, calcoliamo la componente verticale del vettore, essa descrive proprio una sinusoide nel diagramma (x,y), dove x è l'angolo e y è la componente del vettore ossia il seno dell'angolo. Se il moto è uniforme è facile inserire il tempo al posto dell'angolo dato che t = P/2π, dove P è il periodo di rotazione del vettore u.

Bene, questa è una rappresentazione estremamente ovvia e ben conosciuta. Noi, però, vogliamo fare un passo avanti, come mostra la Fig. 2.

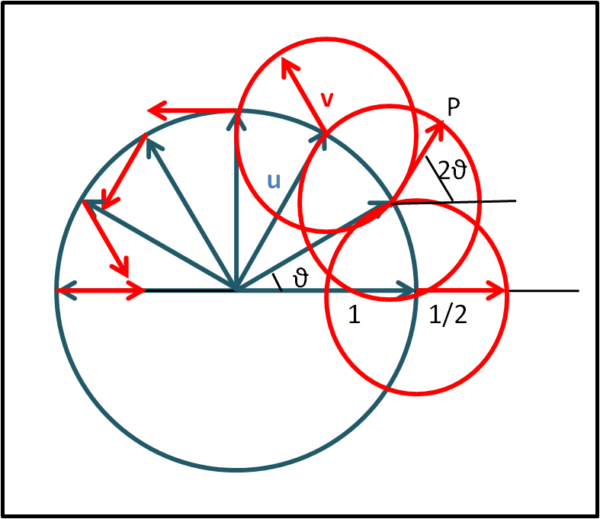
Aggiungiamo un secondo vettore v (rosso) sulla punta del vettore u (azzurro) e lo facciamo ruotare attorno alla punta di moto uniforme, ma con velocità doppia rispetto al vettore azzurro. In poche parole mentre il vettore blu compie un angolo θ, il vettore rosso compie un angolo 2θ. Abbiamo anche dimezzato il modulo del vettore rosso rispetto a quello azzurro. I due vettori partono allineati, ma quello rosso anticipa sempre di più quello azzurro. Ad esempio, quando θ diventa 90°, rispetto alla condizione iniziale, il vettore rosso ha descritto un angolo di 180°.

Non ci resta che sommare i due vettori e individuare il vettore somma V (verde) in Fig. 3.

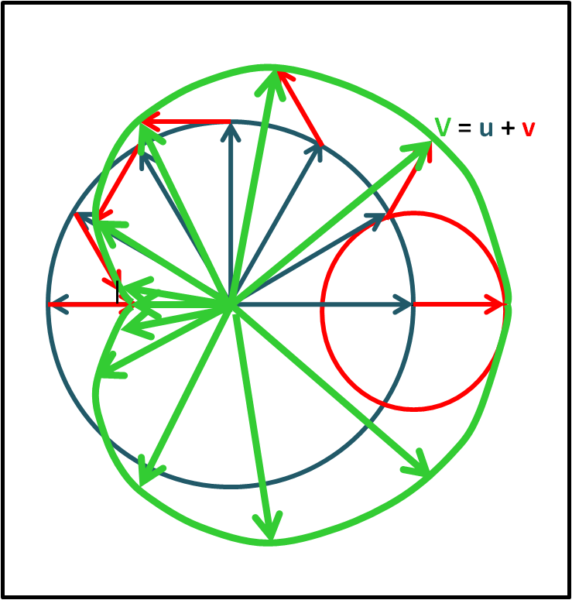
La sua punta descrive una bellissima curva, ma a noi interessa soprattutto rappresentarla nel sistema (x,y). Qual è la componente verticale del vettore verde in funzione dell'angolo θ? Facile a dirsi: è la somma dei seni dei due vettori. Basta allora inserire questa somma nella Fig. 4.

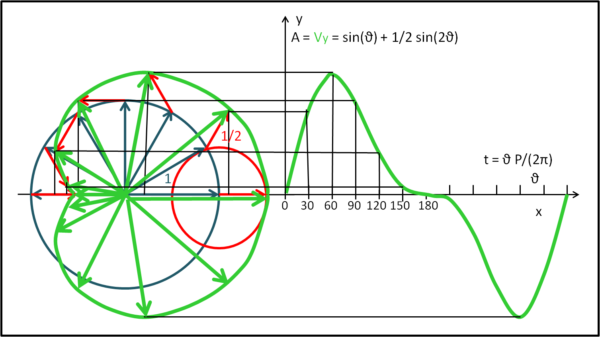
Che cos'è la curva verde nel sistema (y,θ)?

y = sin(θ) + 1/2 sin(2θ)

Non fatemi proseguire con figure fatte a mano... è ormai banale dedurre che se aggiungessi un altro vettore più corto e più veloce aggiungerei un termina alla sommatoria appena scritta, ad esempio:

y = sin(θ) + 1/2 sin(2θ) + 1/4 sin(3θ) + ....

Riassumendo, la rotazione dei vettori nel cerchio di sinistra descrive una serie di Fourier nel sistema di destra.

Io ho preso dei vettori a caso, ma non è certo difficile vedere cosa capita se scelgo un coefficiente diverso, del tipo:

y = (4/π) sin t + 4/(3π) sin (3t) + 4/(5π) sin (5t)

Una serie che conosciamo bene!

Ecco un bel video che mostra quanto detto...

Ed eccone un altro con una serie diversa che approssima una funzione a dente di sega...

Ma, aumentando e scegliendo i vettori da aggiungere si possono ottenere curve estremamente complesse, ma a noi basta proporre il re degli animali, il gatto!

 

La serie di articoli dedicati alla serie di Fourier è disponibile QUI

e fanno parte del corso completo di matematica