L’approccio che cerchiamo di usare, per introdurre lo sviluppo in serie di funzioni, vuole arrivare ad approssimare una data funzione attraverso un semplice polinomio di grado n. E’ un approccio, però, che non troverete nei libri, ma che reputo oltremodo intuitivo e utile per arrivare al nocciolo del problema ed essere poi pronti a una trattazione ben più rigorosa e generale. Nel contempo, le derivate successive incominciano ad assumere un ruolo di primo piano. Divertiamoci un po’ a fare un tentativo che appare campato in aria solo a prima vista…

Facciamo un gioco un po’ strano e senza un vero significato matematico e/o geometrico. Ma, ogni tanto ci si può anche divertire eseguendo tentativi che sembrano del tutto campati in aria. L’importante è che questi tentativi non vengano poi tacciati come teorie alternative o cose del genere. Inoltre, vedremo che questo gioco non è poi tanto assurdo come potrebbe sembrare a prima vista. In qualche modo risponde a una domanda che era stata fatta tempo fa: “Che significato hanno le derivate successive?”.

Consideriamo, allora, una funzione qualsiasi

y = f(x)

La scegliamo in modo che esistano tutte le sue derivate successive e non siano mai zero. Questa frase non è molto strana se pensiamo a una funzione come il seno (o il coseno). La sua derivata vale coseno, la cui derivata è – seno, la cui derivata è – coseno, la cui derivata è seno, e via dicendo… Ovviamente, se calcolata in un certo punto, può anche valere zero, ma non lo è in generale. La stessa cosa vale ovviamente per la funzione e^x, le cui derivate successive valgono sempre e^x.

Ammettiamo quindi che la funzione sia sempre derivabile fino a un ordine n grande a piacere. Esistono perciò e sono finite le derivate

f ’(x), f ”(x), f ^III(x), f ^IV(x), …., f ⁿ(x)

Immaginiamo di conoscerle calcolate nel punto x₀.

Andiamo avanti lentamente e immaginiamo che la nostra funzione sia quella rappresentata nella Fig. 1. Consideriamo un suo punto P(x₀,y₀). Cerchiamo di approssimare la funzione con quel poco che sappiamo.

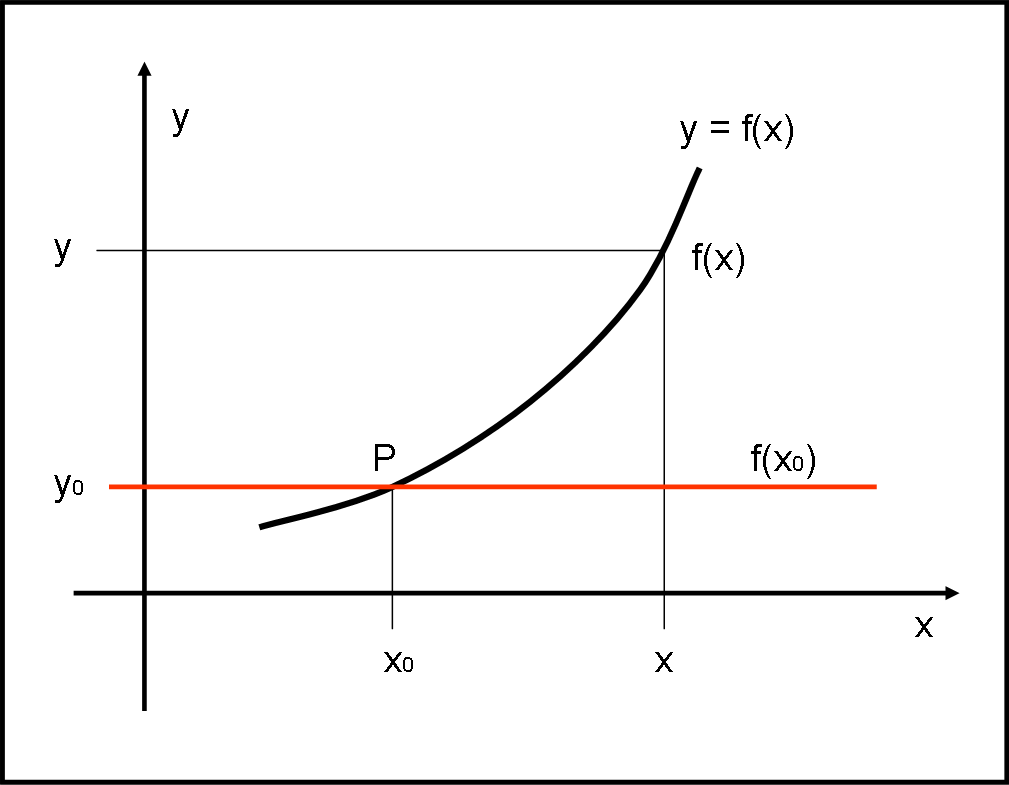
Beh… la prima cosa ovvia è che il punto P appartiene alla curva, perciò deve essere:

y = y₀ = f(x₀)        …. (1)

La (1) non dice molto, ma non vi è dubbio che rappresenta una retta orizzontale, parallela all’asse delle x. Tracciamola nella Fig.1 . Sicuramente abbiamo fatto un passo in avanti: la (1) approssima meglio la nostra funzione (intorno al punto P) di quanto non faccia l’asse delle x. Questa retta ha, sicuramente, un punto in comune con la funzione.

Cerchiamo di migliorare un po’ il risultato…

Scriviamo la retta tangente alla curva nel punto P. Questo lo sappiamo fare senza problemi.

y – y₀ = m (x – x₀) = f ’(x₀) (x – x₀)

Conosciamo x₀, y₀ e f ’(x₀) e possiamo scrivere:

y = y₀ + f ’(x₀) (x – x₀)

o anche:

y = f(x₀) + f ’(x₀) (x – x₀)   …. (2)

Disegniamo, in Fig. 2, la Fig. 1 con l’aggiunta della tangente in P.

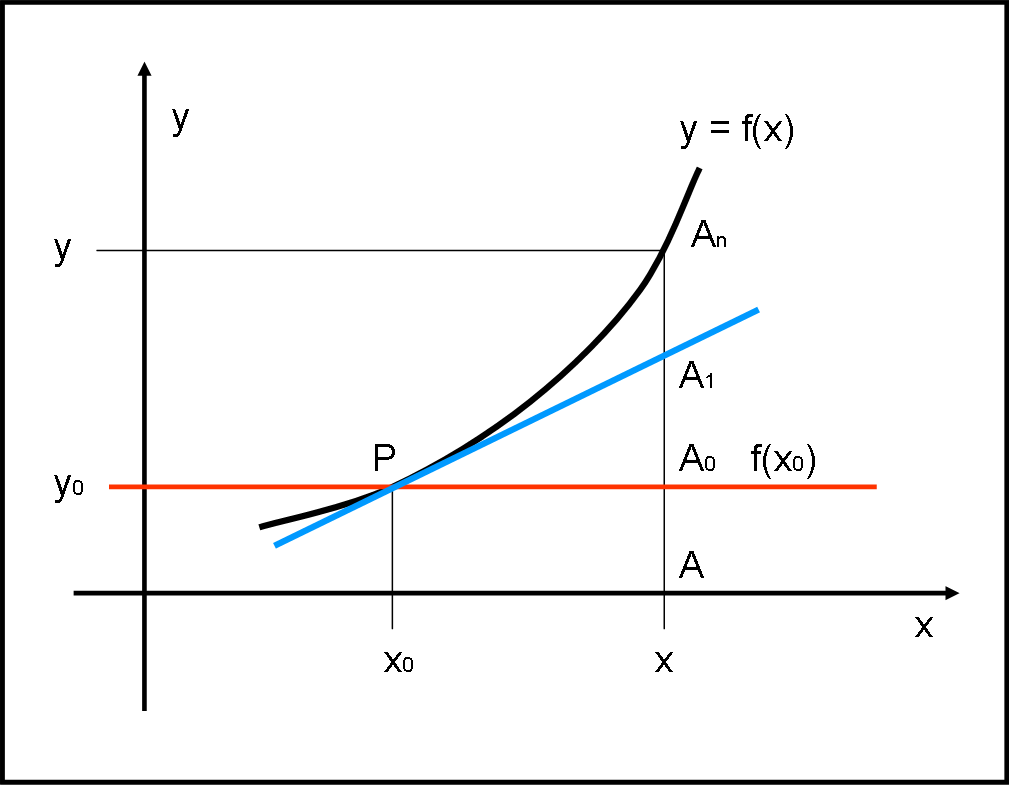
Beh… non possiamo che concludere, nel nostro piccolo, che la (2) approssima la  funzione molto meglio della (1). Facciamo qualche riflessione grafica, considerando i punti A sull’asse x; il punto A₀ sulla parallela all’asse x, passante per P; il punto A₁ sulla tangente; il punto A_n sulla curva relativa a f(x). Ogni punto ha come ascissa una qualsiasi x (meglio se vicina a x₀). Risulta subito che:

AA_n = AA₀ + A₀A₁ + A₁A_n

Ossia:

f(x) = f(x₀) + f ’(x₀) (x – x₀) + A₁A_n

E anche

f(x) - f(x₀) - f ’(x₀) (x – x₀) = A₁A_n

Possiamo anche chiamare A₁A_n = R e chiamarlo “errore”, commesso approssimando la funzione con la retta tangente in P. Un errore che tende naturalmente a ZERO per x che tende a x₀. A questo riguardo potremmo anche dire (senza sbagliare concettualmente) che se la retta y = y₀ ha un solo punto in comune con la funzione (P),  la tangente in P ha "due punti" in comune ed entrambi coincidono con P. In qualche modo la tangente sembra “adattarsi” di più alla funzione nel punto P di quanto non faccia la retta parallela all’asse x. E’ un po’ il discorso che avevamo fatto per i massimi e minimi e per i flessi… ricordate? In fondo, se guardiamo la figura ruotandola in modo che la tangente diventi l’asse delle x, facendo coincidere il punto P con O, quest'ultimo diventa una specie di minimo (e annulla oltre che la funzione anche la derivata prima).

Ricordiamo, poi, un punto essenziale sul quale ci si confonde spesso. Si dice che la derivata prima rappresenta la tangente alla curva in un certo punto. In realtà non è esatto. Bisognerebbe dire che la derivata prima rappresenta il coefficiente angolare della retta tangente, ossia ha un senso solo se è calcolata nel punto e diventa un coefficiente numerico. In altre parole (sto tirando l’acqua al mio mulino per dare forza al gioco che inizierà tra poco), la derivata che compare nella tangente (che approssima la curva in P) è solo e soltanto un coefficiente numerico. Pensateci un po' sopra e andiamo pure avanti…

Riguardiamo con attenzione la (2) e il suo significato geometrico rappresentato in Fig. 2.

Cosa potremmo fare per approssimare ancora meglio la funzione di partenza? Non certo cambiare la retta, ma cercare di utilizzare una curva che si avvicini ancora di più alla f(x). Beh… se dobbiamo usare una curva, la cosa migliore è quella più semplice, ossia un polinomio di secondo grado, cioè una parabola. Potremmo anche chiamarla parabola osculatrice nel punto P. Essa avrebbe tre punti in comune con la f(x), tutti e tre coincidenti con P. Questa “pazza” idea sembra essere confermata dall’andamento della (2), la quale è formata da un termine noto, y₀ = f(x₀), ossia la funzione stessa calcolata in x₀, moltiplicato per (x – x₀) elevato a ZERO e da un coefficiente (la derivata prima calcolata in x₀) moltiplicato per (x – x₀) elevato all’esponente UNO. Come fare per farla diventare una parabola? La prima idea che “mi” viene in testa (no, non credeteci, è già venuta ad altri prima che a me!) è aggiungere un termine in cui compare (x – x₀) elevato all’esponente DUE.

Per cosa lo moltiplichiamo? Tanto vale provare: per la derivata seconda di f(x), sempre calcolata in x₀. Ciò che sicuramente si ottiene è qualcosa come quella rappresentata in Fig. 3 (curva verde) che possiamo chiamare parabola osculatrice. Siamo sicuri che questa curva approssimi meglio la curva? Beh… direi proprio di sì. Se non altro, il termine di secondo grado ci assicura che la nostra parabola tende a y₀ più velocemente di quanto non faccia la retta tangente, che è di primo grado in x, al tendere di x verso x₀.

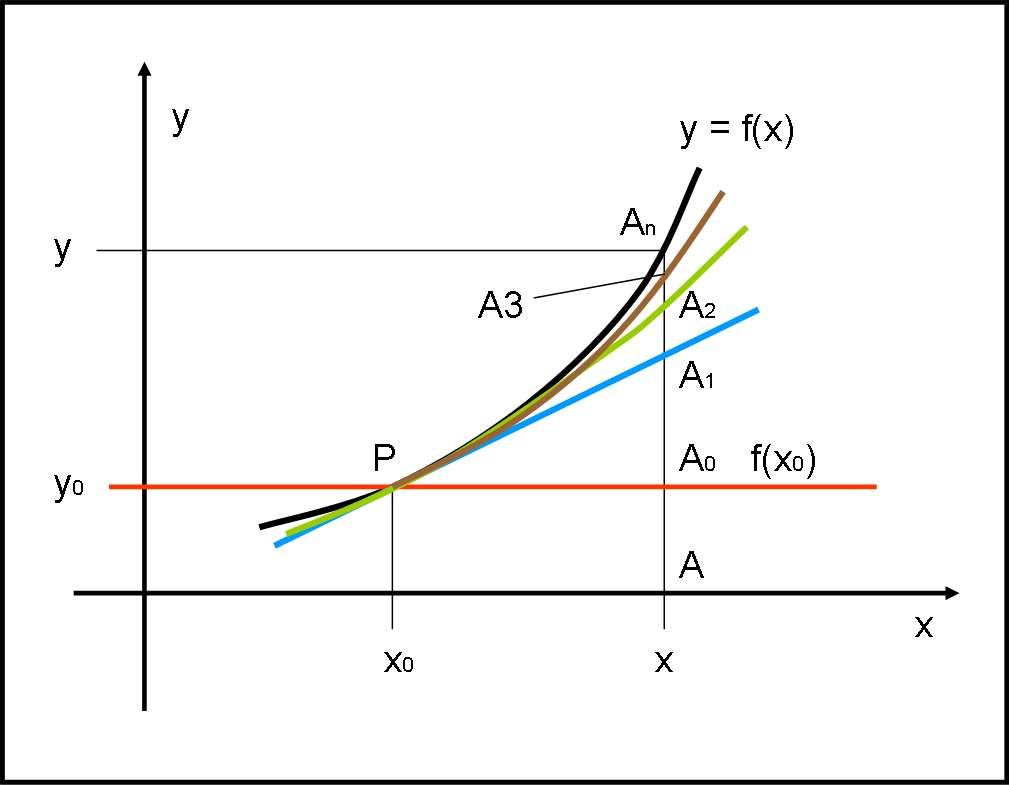
La funzione che dovrebbe approssimare la f(x) meglio della tangente sarebbe data da:

f(x) = f(x₀) + f ’(x₀) (x – x₀) + f ”(x₀) (x – x₀)² + A₂A_n

A₂A_n rappresenta la parte che ci manca per un’approssimazione perfetta della nostra parabola con la funzione di partenza. Esso è chiaramente più piccolo di quello precedente. Ossia R diminuisce.

Una trattazione più accurata e meno campata in aria potrebbe fare uso del calcolo differenziale, ma andrebbe ben oltre i nostri scopi e quindi accontentiamoci di queste conferme molto grossolane. Ci torneremo sopra tenendo per mano il teorema di Lagrange e tutto sarà più logico.

A questo punto, tanto vale insistere per la stessa strada. Possiamo continuare con la derivata terza e aggiungere un termine. Alla nostra funzione costruita attraverso un polinomio (eh sì, stiamo usando solo potenze di x moltiplicate per coefficienti numerici…), aggiungiamo il termine di terzo grado:

f ^III (x₀) (x – x₀)³

La nostra funzione che tende ad approssimare la f(x) in un intorno del punto P, è diventata:

f(x) = f(x₀) + f ’(x₀) (x – x₀) + f ”(x₀) (x – x₀)² + f ^III(x₀) (x – x₀)³ + A₃A_n

Una bella cubica (cubica osculatrice, chiamiamola così…) che approssima ancora meglio la nostra funzione di partenza f(x) in un intorno di P (curva marrone in Fig. 3). L’errore che si commette diventa sempre più piccolo e possiamo dire con certezza che deve essere un infinitesimo di ordine superiore a TRE. Un errore che possiamo ormai permetterci di chiamare “resto”.

Ovviamente, possiamo proseguire fino ad arrivare all’ordine n che preferiamo e che ci regala un errore più piccolo rispetto alle nostre esigenze.

Tutto bene? Nemmeno per sogno! Purtroppo, i primi due termini che ci sono serviti per il nostro gioco non ci regalano informazioni sul coefficiente numerico che deve veramente moltiplicare  (x –x₀) elevato alle potenze successive. Non ci resta che fare una cosa, molto banale ma illuminante e decisiva. Applichiamo la nostra “fantasia” matematica a una funzione che sia davvero un polinomio. Ad esempio una bella cubica e vediamo se funziona veramente. Se funziona per lei siamo abbastanza sicuri che funzionerà anche per funzioni diverse dai polinomi. Lagrange ci aiuterà di nuovo per passare da fantasia a realtà.

Bene, la prossima volta faremo questo tentativo.

Sì, lo so, abbiamo fatto un po’ di pseudo-matematica, molto empirica e poco rigorosa. Abbiamo veramente scherzato? Mica tanto e, comunque, abbiamo introdotto lo sviluppo in serie in modo estremamente semplice e intuitivo. Inoltre le derivate successive acquistano un significato “quasi” geometrico, dato che sono i coefficienti dei termini di grado equivalente.

Chi storce un po’ il naso, vedrà che correremo ai ripari, sempre grazie a Lagrange (uffa!)

 

QUI il capitolo precedente

QUI il capitolo successivo

QUI l'intero corso di matematica