La serie dedicata alle Numerazioni non decimali è inserita in Matematica e Geometria

 

Questo articolo è il seguito di quello dedicato alla nascita dei numeri. In altre parole, scelti i simboli impariamo a CONTARE.

Abbiamo i nuovi simboli e possiamo cominciare a contare con qualsiasi base si voglia...

Torniamo a descrivere l'operato del vecchio saggio e di due altre "scelte" relative al numero di dita che si vogliono scegliere come base.

Abbiamo visto che il saggio aveva segnato su una tavola le dita delle due mani per indicare le conchiglie avute in dono e che poi aveva utilizzato un'altra tavola di pietra per segnare quante volte aveva completato la prima tavola. Se le conchiglie aumentavano, doveva passare a una terza tavola e così via. Ciò che era cambiato rispetto al primo tentativo erano solo i simboli per indicare quante dita avesse alzato. In particolare un dito alzato aveva simbolo 1, due dita alzate il simbolo 2, e così via... nove dita alzate il simbolo 9.

A questo punto, l'arrivo di una nuova conchiglia avrebbe causato il sollevamento di tutte le dita delle due mani e avrebbe comportato il simbolo 1 nella seconda tavola, azzerando la prima tavola, dove avrebbe ricominciato a segnare 1, 2, 3, ...., 7, 8 e 9. Una nuova conchiglia l'avrebbe costretto a far diventare 2 il simbolo della seconda tavola, mentre si sarebbe di nuovo  azzeratala la prima tavola. Quando la seconda tavola avesse raggiunto il simbolo 9, si sarebbe passati a una terza tavola.

Nella Fig. 6 viene identificata una certa quantità di conchiglie avute in dono

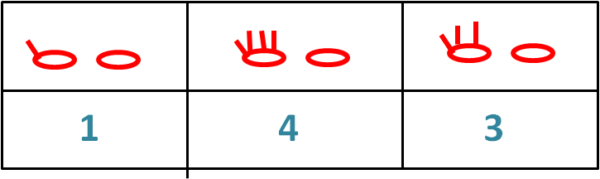
In alto, i simboli primitivi con le due mani con le dita che si alzano. Nella prima tavola si stanno completando le due mani e siamo giunti al simbolo 3. Nella seconda tavola il simbolo con un solo dito equivale a una prima tavola completata. Ve ne sono un certo numero, che viene  trasformato nel simbolo 4. Nella terza tavola si ricorda che è già stata completata una volta la seconda tavola. Ne segue che il numero corrispondente è un dito sollevato, che si trasforma in 1.

Alla fine otteniamo il numero 143, che vuol dire che sono state ricevute (o -se volete- CONTATE) 143 conchiglie, ossia sono state alzate 143 dita. Un gran passo in avanti!

Questo sistema di numerazione è stata chiamato in base 10, dato che per spostarsi da una tavola a quella successiva bisogna aver completato le 10 dita e poi dieci volte le 10 dita e poi 10 volte 10 volte le 10 dita, ecc. La prima tavola prende il nome di tavola delle unità, la seconda delle decine (ossia conta quante volte la prima tavola ha raggiunto il numero 10), la terza delle centinaia (ossia conta quante volte la seconda tavola ha raggiunto dieci volte dieci).

Ovviamente non esiste un simbolo per dieci, in quanto i simboli vanno da 0 a 9 e l'aggiunta di una conchiglia  dopo il 9 annulla la prima tavola (0) e aggiunge 1 nella seconda (1). Il simbolo per il numero 10 viene indicato dal simbolo 0 nella prima tavola e dal simbolo 1 nella seconda tavola.

A questo punto seguiamo passo dopo passo, in Fig. 7,  l'azione di contare le conchiglie che viene eseguita dal vecchio con i nuovi simboli. Immaginiamo di dare una conchiglia alla volta e vediamo cosa viene fuori alla fine... Consideriamo 21 conchiglie, date una alla volta. Una specie di gatto che si morde la coda, dato che sappiamo già il risultato finale (21), utile, però, per passare a due basi diverse.

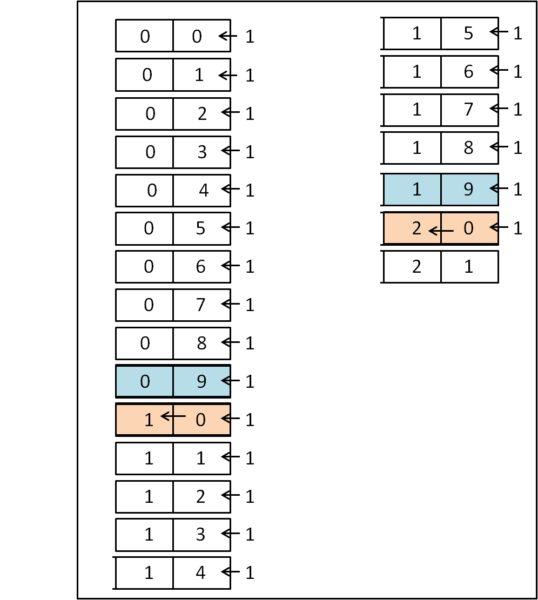
Ad ogni passo aggiungiamo una conchiglia. Fino a 9 conchiglie si usano i nuovi simboli. Poi arriva il momento critico... Se aggiungiamo una conchiglia si completa  la prima tavola che torna ad azzerarsi, mentre nella seconda tavola si inserisce il simbolo 1. Nuovo completamento della prima tavola e aumento di 1 nella seconda tavola, e via dicendo.

La stessa tabella può essere disegnata in modo più "geometrico" nella Fig. 8.

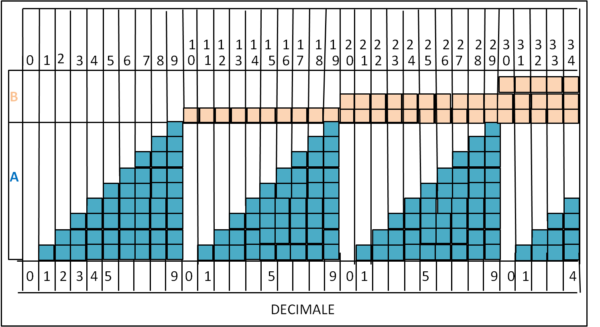
Nell'asse orizzontale si aggiungono, una alla volta, le conchiglie, il cui "numero" cresce fino a 9. A quel punto la prima tavola (A) è completata e si riporta 1 sulla seconda tavola (B). I numeri in base 10 si leggono lungo ogni singola colonna, dall'alto verso il basso.

Nel caso della base decimale, la Fig. 8 è praticamente inutile, ma non lo è più se cambiamo la base e utilizziamo la stessa procedura. In Fig. 9 riportiamo la numerazione quinaria (base 5).

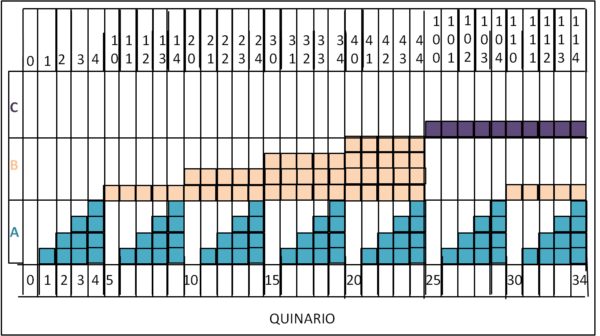
I simboli utilizzati vanno da 0 a 4 (come prima andavano da 0 a 9). In basso possiamo portare i numeri in base 10 (ormai li conosciamo bene), mentre per ogni conchiglia in più dobbiamo ricordarci che la prima tavola (A) si completa inserendo 4 conchiglie. A quel punto si azzera e si aggiunge il simbolo 1 nella tavola B. Le operazioni da svolgere sono più semplici a vedersi che non a scriversi. In alto, per ogni colonna, abbiamo i simboli relativi. Ad esempio, al decimale 21 corrisponde il quinario 41.

La Fig. 8 permette in pratica di illustrare la procedura del "contare in base 5", ma anche di trasformare immediatamente ogni decimale in quinario (e viceversa). So benissimo che esistono programmini già fatti in rete che trasformano ogni numero da una base ad un'altra, ma volete mettere il piacere di giocare graficamente con le varie numerazioni?!

Dal punto di vista "visivo" la numerazione binaria (quella che riescono a capire i computer) è sicuramente la più "artistica". Esistono solo i simboli 0 e 1 e quindi il passaggio da una tavola all'altra è estremamente rapido e -spesso- causa una certa confusione. La sua rappresentazione è riportata in Fig. 10

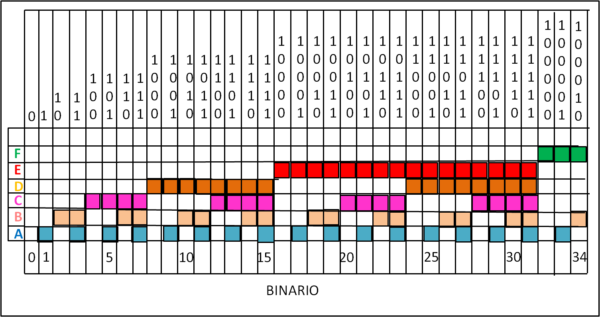
Il passaggio da numeri decimali a binari è immediato e, inoltre, si scoprono "figure " che si ripetono e che si ingrandiscono. Ad esempio i numeri azzurri (tavola A) cambiano continuamente tra 0 e 1. Quelli rosa (tavola B) fanno lo stesso, ma a coppia (due pieni e due vuoti). Quelli della tavola C vanno di 4 in 4; poi (tavola D) di 8 in 8 e (tavola E) di 16 in 16, e via dicendo. Se partissimo da numeri grandissimi ci apparirebbe una figura simile, in qualche modo, a un frattale...

Il passaggio da un sistema a un altro può essere ottenuto in modo altrettanto semplice, ma con l'intervento di un'operazione (la divisione, in particolare, da base 10 a base 2). Un'operazione che comporta dei "resti", proprio quelli che hanno aiutato i prigionieri con il cappello a salvarsi.

Tuttavia, per adesso, non abbiamo ancora introdotto le operazioni, ma solo la capacità di contare con basi diverse. Potremmo anche introdurre le 4 operazioni, ma, probabilmente, diremmo qualcosa che è ben conosciuto da tutti. Possiamo, perciò, fermarci qui...