Questo articolo è inserito nella pagina "La caduta libera" 

 

Semplifichiamo di molto un argomento piuttosto complesso che permette ai paracadutisti e agli acrobati del cielo di lanciarsi con relativa tranquillità.

Se qualcuno pensasse di provare l'ebbrezza della caduta libera buttandosi da un aereo, ci arriverebbe vicino, ma per pochissimo tempo. Possiamo dire con tranquillità che cadendo da un aereo i corpi non viaggiano alla stessa velocità come dimostrato da Galileo. Non per niente i primi astronauti provarono proprio a far cadere una pallina di ferro e una piuma sulla Luna, dove le previsioni di Galileo (e non solo) furono confermate, cancellando per sempre l'idea aristotelica. Infatti, è necessario che si cada nel "vuoto" e non certo in una atmosfera come quella terrestre. Provate a mettere una mano fuori dalla macchina lanciata a grande velocità e ditemi se sentite qualcosa oppure no. Sicuramente direte di sì, in quanto l'aria diventa un vero ostacolo per la vostra mano e sentite chiaramente che oppone una resistenza che aumenta all'aumentare della velocità.

Siamo di fronte all'attrito viscoso e, in particolare, al moto di un corpo attraverso un fluido.

Cosa capita, allora, al nostro paracadutista? Inizia la sua caduta libera che, in prima approssimazione e con accelerazione di gravità g considerata costante, non è altro che un moto uniformemente accelerato. Rimanendo costante l'accelerazione, deve, ovviamente, aumentare la velocità di caduta che raggiungerà il suo massimo quando il paracadutista toccherà il suolo (senza avere aperto il paracadute).

Tuttavia, dopo un breve intervallo di tempo, in cui la velocità è molto piccola, la forza di attrito inizia ad opporsi alla forza di gravità. Questa forza di attrito sembra proprio venire incontro al paracadutista, in quanto cresce al crescere della velocità. Ne segue che la forza di gravità si trova di fronte una resistenza che si oppone sempre più al moto di caduta. Fino a quando? Beh, molto facile dare la risposta: "Fino a quando l'attrito riesce ad avere un valore pari a quello della forza di gravità".

In quel momento l'accelerazione totale si annulla e la velocità raggiunge un valore costante. Questa velocità prende proprio il nome di velocità limite o -se preferite- velocità terminale (dall'inglese terminal velocity). Attenzione, però, a non illudersi più di tanto, dato che è una velocità costante, ma sempre molto alta e supera mediamente i 200 km/h, sufficienti a fare poltiglia del paracadutista. Tuttavia, il raggiungimento di questa velocità dà praticamente il via all'apertura del paracadute.

Bene, vediamo di scrivere qualche formula che ci dia un'idea più chiara di ciò che avviene sia senza che con un paracadute.

Il calcolo della velocità limite è estremamente facile, dato che per ricavarla non dobbiamo fare altro che uguagliare forza di gravità F_G e forza di attrito F_R. Ma... quanto vale la forza di attrito? Questa è la parte più complicata, dato che essa dipende sia dal fluido che viene attraversato, sia dalla forma dell'oggetto che cade. Ma, come già detto,  essa è soprattutto legata alla velocità.

Possiamo scrivere semplicemente:

F_R= b v

dove b contiene tutte le caratteristiche del corpo che cade e del fluido che attraversa, da cui:

F_R = F_G

bv = mg

v_L = mg/b

Questa è la velocità limite. Il calcolo di b non è facile e può solo essere approssimato a seconda di cosa cade e dove cade. Per oggetti sferici e con velocità relativamente modeste si può applicare la legge di Stock che dice:

b = 6πηR

dove η è il coefficiente di viscosità del fluido e R il raggio della sfera.

Conoscere il valore limite è importante, ma ancora più interessante è ricavare la legge della velocità in funzione del tempo, anche per sapere quando conviene aprire il paracadute (sempre  che si abbia a ... portata di mano). Per far ciò dobbiamo scrivere la legge del moto e poi integrare per vedere quando e come si raggiunge la velocità limite. In poche parole siamo di fronte a una equazione differenziale.

Ovviamente, l'equazione da considerare è la seconda legge di Newton:

F_G = ma

Possiamo imporre l'accelerazione costante e chiamarla proprio g.

F_G = mg

Il paracadutista, però, risente velocemente dell'attrito viscoso che agisce come forza che si oppone alla gravità. Ne segue che:

F_G - F_R = ma

dove a è l'accelerazione effettiva del paracadutista. Ricordando il valore di F_R, possiamo scrivere:

mg - bv = ma

v è la nostra velocità che è vincolata all'accelerazione a. Ne segue:

mg - bv = mdv/dt

Questa è la nostra equazione differenziale (compare la velocità e la sua derivata) che dobbiamo risolvere.

Isoliamo la derivata:

(mg - bv)/m = dv/dt

E ancora ...

dt/m = dv/(mg - bv)

A questo punto integriamo entrambi i membri dell'uguaglianza:

∫₀^tdt/m = ∫₀^vdv/(mg - bv)

Il primo integrale è esteso dal momento del lancio (t = 0) fino a un certo valore t, mentre il secondo è esteso da v = 0 (momento del lancio) fino a una certa velocità limite v.

Il primo membro vale ovviamente t/m, mentre il secondo è un integrale fondamentale^(*) del tipo

∫dx/(a + bx) = (1/b) ln(a + bx) + c

per cui:

t/m = (-1/b)|ln(mg - bv)|₀^v = (-1/b)(ln(mg - bv) - ln(mg))

Ricordando le proprietà degli integrali

t/m = (-1/b) ln((mg - bv)/mg)

- (bt/m) = ln((mg - bv)/mg)

Per far sparire il logaritmo basta fare l'esponenziale di entrambi i membri

e^{- (bt/m)} = (mg - bv)/mg

e^{- (bt/m)} = 1 - bv/mg

bv/mg = 1 - e^{- (bt/m)}

v = (mg/b)(1  - e^{- (bt/m)})

Ovviamente per t che tende a infinito la velocità tende proprio a mg/b, come già trovato all'inizio.

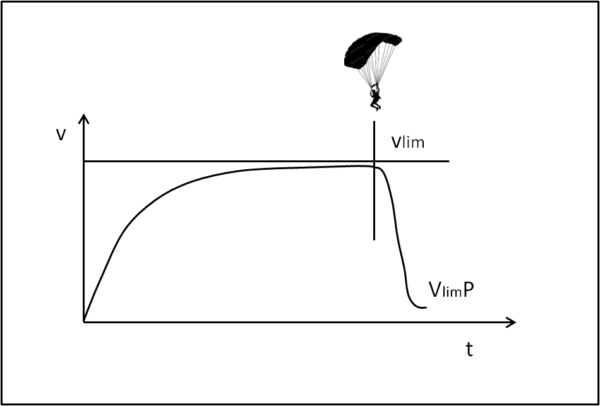
La Fig. 1 illustra l'andamento della velocità in funzione del tempo con la velocità limite che impone un asintoto.

In realtà, così facendo, faremmo arrabbiare un poco Archimede. Ricordiamoci che lui aveva detto e dimostrato che "un corpo immerso in un fluido riceve una spinta dal basso verso l'alto pari  al peso del volume del liquido spostato". Per essere più corretti, allora, dobbiamo introdurre anche questa spinta (S_A) che va ad aiutare l'attrito nel contrasta la forza di gravità. In poche parole:

F_G = F_R + S_A

Sappiamo che

F_G = mg

F_R = 6πηR v

S_A = ρ_AV g

Dove la massa è stata scritta come prodotto tra la densità del fluido ρ_A e il volume V del fluido spostato. Possiamo esprimere anche la massa m, che compare nella forza di gravità, in termini di volume V e di densità del corpo che cade ρ:

ρV g = 6πηR v+ ρ_AV g

da cui si ricava la nuova velocità limite:

vL = V g (ρ - ρ_A)/6πηR

Come si vede, essa aumenta al crescere della differenza tra la densità del corpo che cade e quella del fluido in cui avviene la caduta.

Trascuriamo pure il termine dovuto alla spinta di Archimede e torniamo al nostro paracadutista. Cosa deve fare per divertirsi e non rischiare la vita? Può aspettare tranquillamente di aver raggiunto la velocità limite e a quel punto aprire il suo paracadute. Cosa succede? L'attrito atmosferico aumenta sensibilmente a causa delle dimensioni del paracadute, per cui adesso è l'attrito che supera la forza di gravità. Il corpo in caduta decelera velocemente e la velocità diminuisce altrettanto rapidamente.

Se la velocità decresce, però, deve decrescere anche l'attrito, da cui segue che viene raggiunta una nuova velocità limite quando le due forze si equivalgono nuovamente. Quest'ultima è notevolmente più bassa della prima (pochi km/h) e può accompagnare il paracadutista fino al suolo. La Fig. 2 mostra la velocità del paracadutista fino a terra.

Dobbiamo aggiungere che quanto trattato finora si riferisce a un moto a velocità relativamente bassa, ossia tale che il fluido scorra in modo "laminare". Se la velocità è più alta si passa a un moto in regime "turbolento" con la creazione di vortici, come mostra la Fig.3

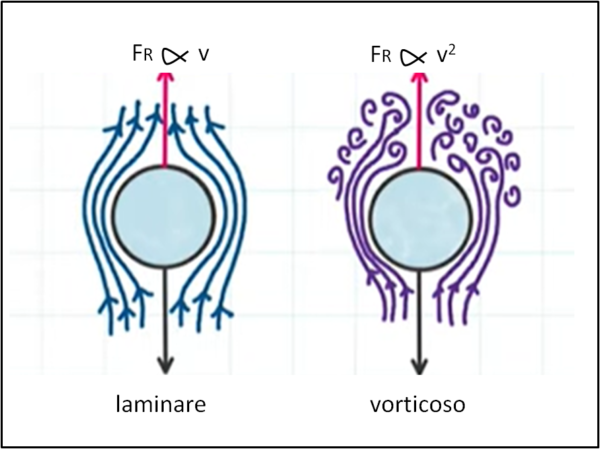
In questo caso, la forza d'attrito è proporzionale alla velocità al quadrato e -detto in modo molto semplificato- essa è uguale  alla radice quadrata di quella precedente, ossia:

v_L = √(mg/b)

Abbiamo trattato l'argomento in modo molto semplificato, sapendo che la faccenda è molto più complicata dato che i coefficienti che intervengono e i regimi raggiunti sono basati su relazioni spesso empiriche.

Comunque, se volete approfondire potete sempre chiedere al vostro amico gatto che, in fatto di cadute, la sa molto lunga, anche senza paracadute.

(*) calcolo dell'integrale fondamentale ∫dx/(a + bx)

∫dx/(a + bx)

u = a + bx

du = b dx

du/b = dx

∫dx/(a + bx) = 1/b∫du/u = 1/b ln(u) = 1/b ln(a + bx) + c