Questa è la soluzione al quiz sui quattro gatti (QUI e QUI), descrittami dalla mia cara miciamica Tigrotta.

Come ben sapete la "mia" cara amica Tigrotta non ama la trigonometria e ancor meno lo sviluppo in serie. Tuttavia, conosce bene la matematica ed è un asso con le derivate e i limiti. La sua soluzione, perciò, è abbastanza particolare, ma efficace.

Il primo passo che compie la vede un po' nervosa, dato che deve seguire l'approccio di qualsiasi topo di passaggio. Ma lei sa benissimo che questo  banale "inizio" le è decisamente utile per stabilire le variabili con cui ha a che fare. Decide perciò di muoversi verso il gatto alla sua sinistra (chiamiamolo G2), lungo il lato del quadrato, sapendo benissimo che nel frattempo anche G2 si è mosso lungo il  "suo" lato del quadrato. Dopo un certo intervallo di tempo t vede perfettamente dove si è portato il gatto G2 e cambia direzione andando verso di lui. Lascia passare un altro intervallo di tempo t e torna a guardare G2 che si è ovviamente mosso. Altro cambiamento di direzione e così via. Ciò che succede lo vediamo in Fig. 1.

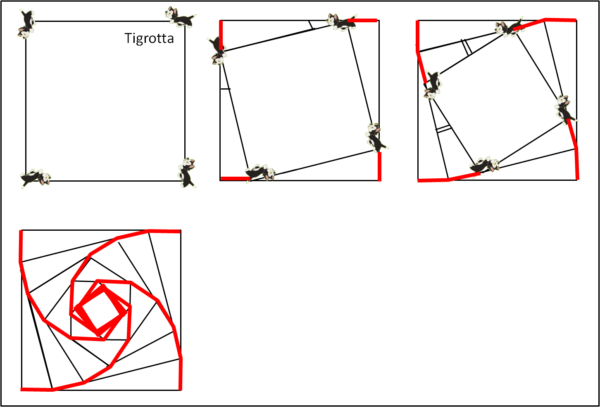
Tigrotta ha già capito cosa succede fin dall'inizio: a un certo punto tutti e quattro i gatti si trovano a distanze tali che la traiettoria rimane sempre uguale a se stessa.

I quadrati successivi, che descrivono un bellissimo insieme di  linee,  continuano fino a che il tempo t, tra un cambiamento della direzione di Tigrotta e il successivo, corrisponde perfettamente al tratto rettilineo che deve percorrere.

Ne segue che, da quel momento in poi, il moto non può che essere ripetitivo e senza sbocco alcuno. In altre parole, la lunghezza del lato del quadrato rimane costante, anche se lo spazio percorso aumenta. In quel gioco inutile e idiota ci possono cadere solo animali inferiori come, ad esempio, certi uomini odierni... basta che glielo ordini facebook!

Molto bene, Tigrotta non ha bisogno di altri dati e decide di fare un grafico (Fig. 2) dove nell'asse delle ascisse mette il tempo che è anche lo spazio percorso dato che la velocità è costante e si può porre uguale a 1, mentre nell'asse y inserisce la lunghezza del lato del quadrato che compare, ad esempio, ad ogni intervallo t = 0.2.

Tigrotta può disegnare facilmente il grafico senza bisogno di effettuare realmente questa serie di movimenti che sa benissimo non portarla a nessuna conclusione pratica. Nel grafico, vede dei punti che appartengono sicuramente a una funzione, ma lei non ha alcun interesse a determinarla (i gatti puntano al sodo...). Per determinare i vari lati L, le basta conoscere il teorema di Pitagora.  Nella Fig. 3 è indicato il triangolo legato al primo cambiamento di direzione di Tigrotta.

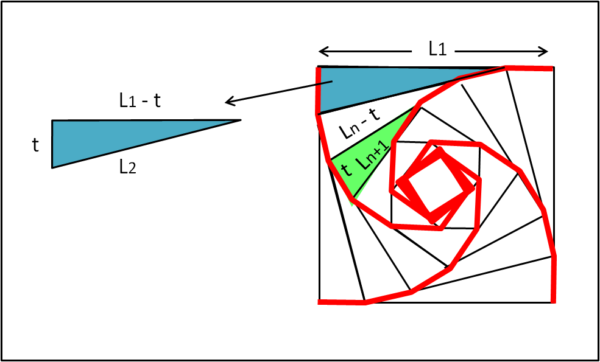
Il suo cateto maggiore è pari a L1 - t, mentre quello minore è proprio uguale a t.

Con Pitagora ottiene

L₂ = √(t² + (L₁– t)²)

E, successivamente, ripete l'operazione per tutti i cambiamenti n di percorso

L_n+1 = √(t² + (L_n – t)²)                    .... (1)

Dalla Fig. 3 Tigrotta può facilmente determinare la pendenza P di ogni tratto della funzione incognita L(x).

Essa è data da:

P = dy/dx = dy/t

P = (L_{n +1} – L_n)/t                        .... (2)

Questa espressione è ovviamente valida  per ogni tratto di lunghezza t.

A questo punto Tigrotta inserisce la (2) nella (1), ottenendo:

P = (√(t² + (L_n – t)²) – L_n)/t                 .... (3)

Non le resta che far tendere t a zero per ottenere la pendenza della funzione in questo caso limite che è proprio quello richiesto dal problema (il gatto deve seguire istante per istante il gatto alla sua sinistra, ossia t deve tendere a zero).

Tigrotta è molto sicura del fatto suo e ha solo un attimo di esitazione quando va a calcolare

lim_t→0(√(t² + (L_n – t)²) – L_n)/t

e si trova davanti una forma indeterminata 0/0.

Nessun problema per lei che ben conosce il teorema di De l'Hopital  e  va a nozze con le derivate. Basta infatti derivare numeratore e denominatore e poi passare al limite.

Quasi magicamente trova

lim_t→0d/dt(√(t² + (Ln – t)²) – Ln)/(dt/dt) = - 1             (Provare per credere ...)

Questo vuol dire che la pendenza è costante e che, di conseguenza, la funzione non è altro che una retta del tipo:

y = - x + b

Ma la retta deve ovviamente passare per L1 di coordinate (0,1), ossia:

per  x = 0, y = 1 e quindi b =1

La retta è , perciò:

y = - x + 1

Ossia all'atto del ricongiungimento dei 4 gatti

x = 1

La Fig. 4 mostra come diventa la nostra funzione incognita per t = 0.

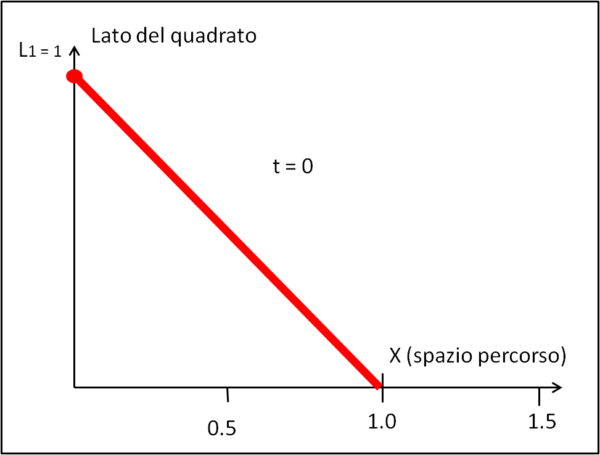
Ne segue che, per simmetria di percorso, i gatti devono incontrarsi al centro del quadrato e che la distanza, da loro percorsa, è proprio uguale al lato del quadrato iniziale di lunghezza unitaria. Il tutto ottenuto senza introdurre curve strane come spirale logaritmica,  sviluppi in serie, o, tantomeno, quelle antipatiche funzioni trigonometriche.

Sapete come sono i gatti quando decidono di non fare qualcosa. Certe cose, Tigrotta, non le vuole proprio imparare, ma, in compenso, conosce perfettamente la meccanica quantistica e la capisce anche! Ha detto che un giorno me la spiegherà, ma mi è sembrato che avesse un sorriso un po' ironico.