Questo articolo fa parte della serie "Disegnare in tre dimensioni: tra storia e pratica"

 

Questo articolo avrebbe dovuto storicamente essere pubblicato per primo, in quanto rappresenta il vero inizio della geometria descrittiva. Noi abbiamo invece trattato abbondantemente sia della prospettiva che dell'assonometria che, in qualche, modo erano già state usate nei secoli in modo spesso solo empirico (a parte la prospettiva che dominò la rappresentazione grafica e non solo nel primo quattrocento).

Tuttavia, abbiamo visto che la prospettiva permette una visione praticamente perfetta della realtà e, quindi, non può che deformare le forme e rendere abbastanza misteriose le vere lunghezze degli oggetti considerati. L'assonometria cerca di mediare misure reali con visione reale, ma è costretta a qualche gioco di prestigio per soddisfare sia gli artisti che i tecnici.

Anche se l'abbiamo sempre presa per buona, la vera raffigurazione di un qualsiasi oggetto tridimensionali e su un unico piano sta nelle mani delle proiezioni ortogonali. Esse sfruttano i tre piani delimitati dagli assi ortogonale x, y e z per proiettare su di essi, attraverso rette perpendicolari, le tre facce di un certo solido.

In realtà, però, anche questo modo di presentare una figura non ci dà una visione completa delle varie facce del solido. Prendiamo ad esempio un semplice parallelepipedo, dove, però, ognuna delle sue facce contenga un motivo diverso (o anche tratti aggettanti o rientranti). Per una visione veramente completa ed esauriente di tutte le misure necessarie a definire il solido dovremmo utilizzare ben 6 facce, ribaltate, alla fine, su un unico piano. Vediamo un esempio in Fig. 1

Abbiamo il nostro parallelepipedo verde (abbiamo trascurato la possibilità di motivi aggiuntivi) e lo inseriamo all'interno di una scatola trasparente (con gli spigoli rossi). Ogni faccia del parallelepipedo di partenza viene proiettata ortogonalmente su una faccia della scatola, ottenendo così 6 proiezioni che possono essere rappresentate su un unico piano effettuando gli opportuni ribaltamenti.   Se proiettare un parallelepipedo con le facce parallele ai piani di riferimento è abbastanza facile, lo è molto meno inclinare il solido in modo casuale e, magari, inserirne un altro e cercare di visualizzare la loro intersezione.

Torniamo, allora, indietro di circa due secoli e mezzo e parliamo nuovamente di quel mago del disegno  che è stato Gaspard Monge.

Gaspard Monge è stato sicuramente un rivoluzionario, sia perché partecipò attivamente alla rivoluzione francese sia perché fu il primo a ideare un sistema di proiezione ortogonale in modo da rappresentare qualsiasi oggetto su un solo piano. Anche se oggi appare come opera banale e ovvia, non lo  seconda metà del 1700. A tal punto che il grande Lagrange ebbe a dire: "Prima di sentire Monge non sapevo di conoscere la geometria descrittiva". La facilità con cui Monge passava dalle idee alla pratica gli faceva dire: "Le mia dita traducono il mio pensiero con una fedeltà geometrica".

Il vero inizio della geometria descrittiva vedeva la proiezione di una figura geometrica solo su due piani tra loro perpendicolari che poi si aprivano in modo da presentarne uno solo. Molto semplicemente, si può pensare a un libro tenuto in orizzontale, aperto a 90°, in modo da formare due piani tra loro perpendicolari (quello orizzontale detto pianta e quello verticale prospetto). La figura viene proiettato ortogonalmente su questi due piani e, infine, si apre completamente il libro la cui doppia pagina è diventata un solo piano in cui è rappresentato il solido.

Questo metodo fondamentale (meno semplice di quello che potrebbe sembrare) può essere utilizzato sempre, tranne che per configurazioni che abbiano bisogno di una proiezione laterale. L'aggiunta di quest'ultima porta proprio alle attuali proiezioni ortogonali.

Entriamo così nel metodo originario di Monge, chiamato oggi metodo delle due proiezioni ortogonali, il quale permette di rappresentare in un solo piano gli enti geometrici sia semplicissimi che estremamente complessi, fornendo praticamente tutti i dati per ricostruire la figura che si vuole rappresentare.

Prima di iniziare dobbiamo ricordare che per una corretta comprensione di questo metodo è necessario indicare con precisione punti e linee fondamentali. Ciò comporta una certa fatica mnemonica e pratica.

Il punto

Iniziamo proprio dall'entità geometrica più semplice. Tuttavia, anche se sembrerebbe del tutto inutile, fatemi disegnare le operazioni da fare per ottenere il piano finale di rappresentazione, seguendo quanto detto poco fa (Fig. 2).

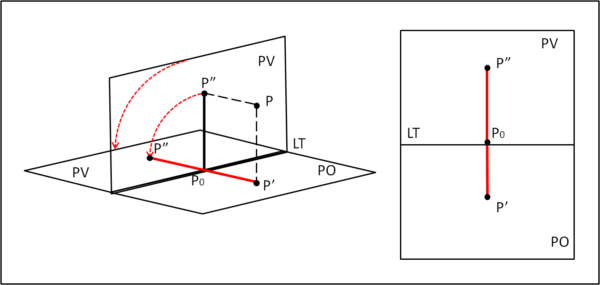
L'intersezione tra i due piani ortogonali viene chiamata Linea di Terra (LT), mentre il piano inizialmente orizzontale è detto PO e quello verticale (da ribaltare) PV.  Teniamo ben presente che la figura da proiettare si intende sempre appartenente al diedro della figura. Quest'ultimo contenga, perciò, anche il punto P. Basta proiettarlo ortogonalmente sui due piani e poi aprirli. Il punto viene indicato dalle sue due proiezioni  P' e P" oltre che dai segmenti perpendicolari alla linea di terra che si incontrano ovviamente nel punto P0.

Sintetizzando, un punto nello spazio (che è quello contenuto nel diedro scelto) viene rappresentato con due punti P' e P", perpendicolari alla Linea di Terra, dove giace P0. La lunghezza PoP' si chiama aggetto, mentre quella tra Po e P" si chiama quota.

Quanto detto vale per un punto qualsiasi. Vediamo in Fig. 3 tutti casi particolari: punto che giace sul PO, punto che giace sul PV, punto che giace sulla LT e, nuovamente, un punto qualsiasi.

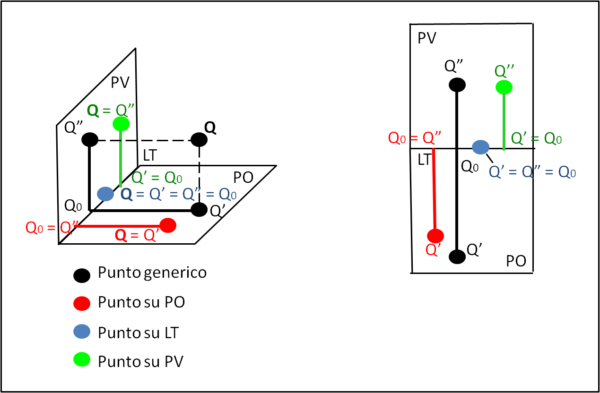
Segmento

Un segmento è definito completamente dai suoi punti estremi, per cui la costruzione di un segmento richiede, in pratica, la costruzione di due punti, le cui proiezioni vengono poi unite nei due piani PO e PV.  In poche parole, le proiezioni del segmento nei due piani fondamentali sono ancora segmenti. La Fig. 4 illustra la costruzione di un segmento qualsiasi posto nel diedro di riferimento.

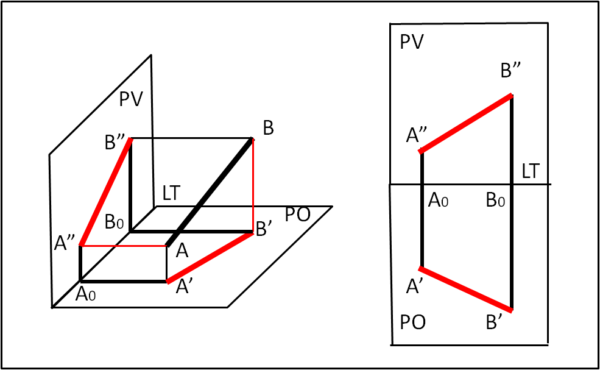
E' sicuramente banale, ma resta comunque  interessante costruire la rappresentazione di segmenti particolari (paralleli o perpendicolari a PO e PV, e via dicendo). Riportiamo soltanto il caso in cui A e B siano rispettivamente punti di PO e PV.

La Fig. 5 mostra la rappresentazione del segmento AB.

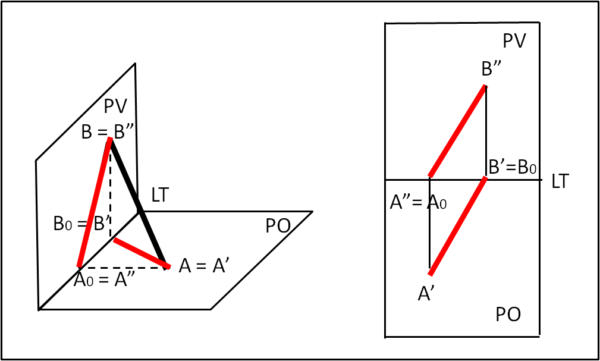
A giace su PO e, quindi, A' = A. Proiettiamolo su PV e otteniamo A" = A0. B giace sul piano PV e, di conseguenza, B = B". Proiettiamolo su PO, ottenendo B' = B0. Non ci resta, adesso, che unire A' con B' e A" con B" e il gioco è fatto!

Un attimo di riflessione: Monge non aveva ancora introdotto l’assonometria che noi stiamo usando per rappresentare le varie figure e comprendere il metodo costruttivo. Lui “vedeva” la figura nello spazio e riusciva a rappresentarla direttamente nei due piani scelti per la proiezione. Oggi sembra facile, ma così non era a fine settecento...

Il problema di dare due punti e chiedere di costruire le proiezioni del segmento che li unisce non ha alcun bisogno della figura assonometrica di sinistra. Lo vediamo in Fig. 6.

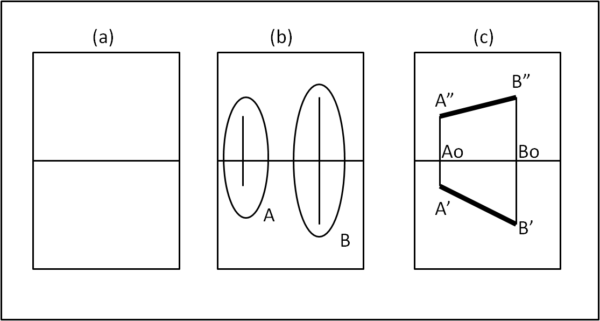
In (a) ho il piano di Monge; in (b) disegno i due punti A e B; in (c) disegno le proiezioni del segmento AB. Sembrerebbe di aver detto una banalità, ma vedremo che per figure più complesse è fondamentale agire in questo modo per non aver bisogno della "inutile" figura assonometrica.

continua ...