Siamo di fronte ai momenti d'inerzia più facili da calcolare.

Iniziamo con il momento d'inerzia di un anello sottile che ruoti attorno all'asse ad esso perpendicolare passante per il centro dell'anello (Fig. 1)

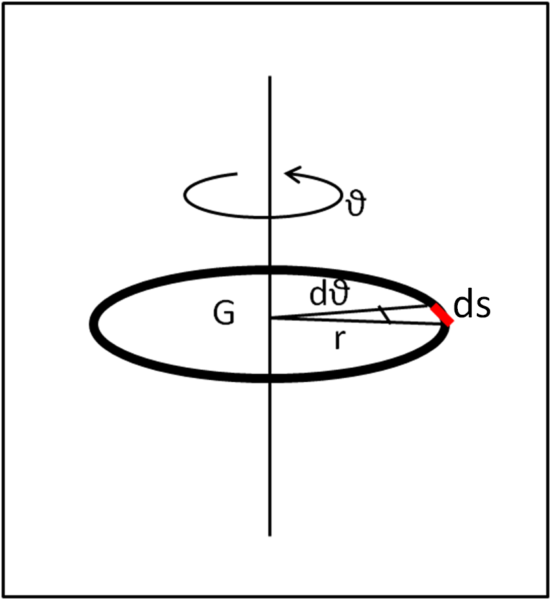
L'anello è formato da punti che stanno tutti alla distanza r dal centro, ossia possiamo dividere il nostro anello in tanti archetti di lunghezza ds. Ognuno di essi corrisponde a un certo angolo dθ. E' immediato scrivere che

ds = r dθ

Notiamo che, d'ora in poi, dovremo trattare, a parità di massa totale M, con tre diversi tipi di densità. Quella volumica che è il rapporto tra massa e volume. Quella superficiale che è il rapporto tra massa e superficie, in quanto si tratterà solo con figure di spessore trascurabile, e quella lineare che è il rapporto tra massa e lunghezza, in quanto sono trascurabili sia lo spessore che l'altezza.

Ogni dl ha una certa massa dm. Come scrivere la massa in funzione di ds? Siamo di fronte a un anello sottile, il che implica che esso abbia solo una dimensione, essendo la larghezza e l'altezza trascurabili. Al posto della densità normale, dobbiamo utilizzare la densità lineare ρ che, in pratica, ci dice che al posto del volume consideriamo solo la lunghezza dell'anello, ossia 2πr :

ρ  = M/2πr                 .... (1)

Da cui segue che la massa dm del nostro archetto di lunghezza ds è data data

dm = ρ r dθ

Il momento d'inerzia dI risulta essere:

dI = dm r² = ρ r dθ r²

Non ci resta che sommare tutti questi archetti infinitesimi. In altre parole fare l'integrale per θ che varia da 0 a 2π

I = ρ r³∫₀^2π dθ = ρ r³ [θ]₀^2π = ρ r³ 2π

Utilizzando la (1)

I = M r²

 

Un po' più difficile è  ottenere il momento d'inerzia di un anello sottile attorno ad un asse ad esso complanare e passante per il centro (Fig. 2)

Tutta la prima parte è analoga al caso precedente, ossia:

dm = ρ r' dθ

dove, però, la distanza r' è la distanza dell'archetto dall'asse di rotazione. Questa distanza varia nuovamente con l'angolo θ e vale

r' = r cos θ

Il momento d'inerzia dI dell'archetto dl è dato da:

dI = dm r'²  = ρ_l r³cos²θ dθ

Non ci resta che integrare tra 0 e π/2 per avere il momento d'inerzia dell'arco che sta nel primo quadrante. Il risultato va poi moltiplicato per 4.

I = 4  ρ_l r³∫₀ ^π/2 cos²θ dθ

Possiamo, però, scrivere cos²θ in altra forma:

cos(2θ) = cos²θ  - sin²θ

cos(2θ) = cos²θ - sin²θ+ cos²θ - cos²θ= 2cos²θ - (sin²θ + cos²θ) = 2cos² θ - 1

cos²θ= (1 + cos(2θ))/2

Il nostro integrale diventa:

I = 4 ρr³∫₀ ^π/2 ((1 + cos(2θ))/2 dθ = 4 ρ r³(∫₀ ^π/2 dθ/2 + ∫₀ ^π/2 cos(2θ)/2 dθ

L'integrale di cos(2θ)/2 risulta essere sin(2θ)/4, infatti se deriviamo quest'ultima relazione abbiamo proprio

d(sin(2θ))/4)/dθ =  2 cos(2θ)/4 = cos(2θ)/2

I = 4 ρ r³(∫₀ ^π/2 dθ/2 + ∫₀ ^π/2 cos(2θ)dθ/2 = 4ρ r³[θ/2+ sin(2θ)/4]₀^π/2

I = 4 ρ r³ (π/4 + 0) = 4 ρ r³π/4 = ρ r³π

Ricordiamo, però, la (1) e, sostituendo, otteniamo:

I = (M/2πr)  r³π

semplificando...

I = 1/2 M r²

Il calcolo potrebbe anche semplificarsi, ma ho voluto usare quello più "laborioso", per maneggiare un po' con gli integrali dato che ne avremo ancora bisogno.

Abbiamo trovato due momenti d'inerzia differenti per uno stesso corpo solido (uno doppio dell'altro), ma questo non ci deve sorprendere in quanto a parità di massa chi domina la situazione è come essa viene distribuita spazialmente. In particolare, poco importa l'angolo legato alla rotazione, ma l'angolo che ci serve per integrare. Il momento d'inerzia dipende dalla massa e dalla forma rispetto all'asse di rotazione, ma rimane una grandezza indipendente dall'effettiva rotazione.

 

A questo punto diventa quasi banale calcolare il momento d'inerzia di un disco sottile. Consideriamo l'asse perpendicolare al disco passante per il centro (Fig. 3)

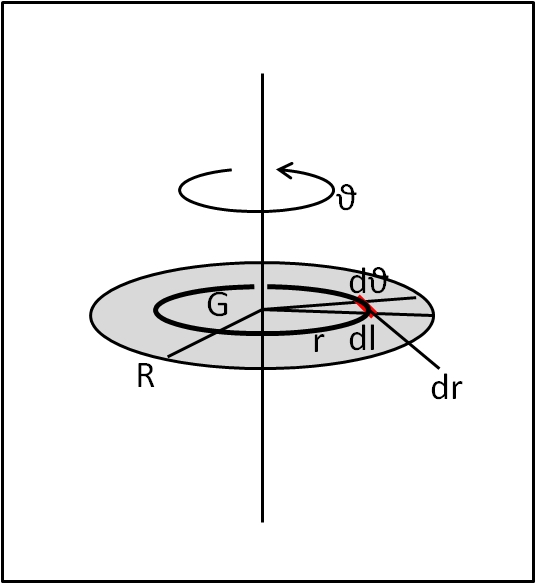
Abbiamo praticamente già a disposizione il momento d'inerzia di un sottilissimo anello del disco (ottenuto integrando secondo θ). Non ci resta altro da fare che sommare tutti gli anelli che hanno raggio compreso tra o e R (raggio del disco).

Ogni anellino ha come momento d'inerzia

dI = dm r²

la massa dm non è altro che la massa dell'intero anellino, ossia:

dm = ρ 2π r dr

Infatti come area dell'anellino possiamo considerare la lunghezza dell'anellino moltiplicato per dr e la densità diventa il rapporto tra massa e area.

Risulta quindi:

dI = (ρ 2π r dr)r² = ρ 2π r³ dr

Non ci resta che integrare il momento d'inerzia dI tra 0 e R.

I = ∫₀^Rρ 2π r³ dr = ρ 2π∫₀^Rr³ dr

I = ρ 2π[r⁴/4]^R₀ = ρ πR⁴/2

Ma la massa dell'intero disco non è altro che la densità moltiplicata per l'area totale (il disco non ha spessore e quindi al posto del volume inseriamo l'area):

M = ρ πR²

Da cui:

I = 1/2 M R²

Se facessimo ruotare il nostro disco attorno a un asse complanare e passante per il centro, concluderemmo che il momento d'inerzia vale:

I = 1/4 MR²

Lascio a voi la determinazione come piccolo esercizio.

Finora abbiamo trattato con densità lineari e superficiali. Passando a solidi tridimensionali la densità diventa quella classica definita dal rapporto tra massa e volume. Dobbiamo notare che, per il calcolo del disco, abbiamo, in pratica, prima integrato con variabile θ e poi con variabile r. Ridendo e scherzando abbiamo toccato gli integrali doppi, anche se solo sfiorati...