Categorie: Fisica classica
Tags: cinematica cinematica mono dimensionale esercizi risolti leggi del moto
Scritto da: Vincenzo Zappalà
Commenti:0
(CIN) Un palazzo e una pietra **
Questo articolo è inserito in Cinematica
Continuiamo con un paio di esercizi sul moto uniformemente accelerato.
Il primo problema è il seguente:
(1) Una pietra cade dal tetto di un palazzo alto H . Quando essa raggiunge un'altezza di H/4 dal suolo sappiamo che toccherà terra dopo 1 secondo. Determinare l'altezza H del palazzo e il tempo totale impiegato dalla pietra per cadere dal tetto al suolo.
Disegniamo il semplice schema di Fig. 1
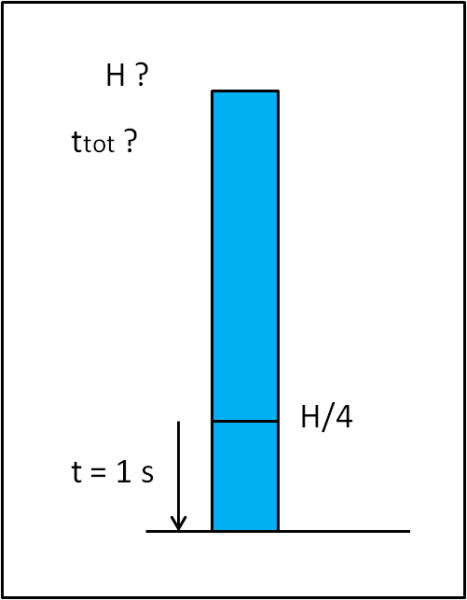
Chi vuol, provare da solo, non legga il seguito...
Dividiamo il problema in due parti: il moto dall'altezza H/4 fino al suolo e il moto dal tetto fino ad H/4.
La pietra arriva in H/4 con una certa velocità v1 mentre toccherà il suolo dopo 1 secondo. Possiamo allora scrivere l'equazione oraria della pietra tra H/4 e il suolo. Poniamo l'origine nel punto corrispondente all'altezza H/4
s = v0 t + 1/2 at2
s è uguale a H/4, t = 1 e a = g
H/4 = v1 + 1/2g
Ne segue che:
H = 4v1 + 2g .... (1)
Non conosciamo, però, v1. Cerchiamo di trovare un'altra relazione tra H e v1.
Facciamo ricorso all'equazione di Torricelli, dato che non c'interessa il tempo (per adesso).
Essa dice che:
v12 = v02 + 2 as
Nel nostro caso vo = 0 (velocità di caduta iniziale), v1 è la velocità con cui arriva in H/4 dopo aver percorso uno spazio pari a
H - H/4 = 3/4 H.
Ne segue:
v12 = 0 + 2 g H(3/4)
v12 = 3gH/2 .... (2)
Facendo sistema tra la (1) e la (2) possiamo trovare l'altezza del palazzo H
v1 = (H - 2g)/4
(H - 2g)2/16 = 3gH/2
(H2 + 4g2 - 4gH)/16 = 3gH/2
H2 + 4g2 - 4gH= 24gH
H2 - 28gH + 4g2 = 0
H = 14g +/-√(142g2 - 4g2) = 14g +/-g √(142- 4) = 137.2 +/- 135.8
Ovviamente, si deve prendere il segno + e otteniamo
H = 273 m
Per conoscere il tempo totale di cauta, basta utilizzate la formula del moto uniformemente accelerato
H = (1/2) g t2
il tempo deve essere positivo
t = √(2H/g)
t = 7.5 s
Ed eccoci al secondo esercizio.
(2) Abbiamo nuovamente un palazzo alto, questa volta, solo 20 metri. Siamo sul tetto e lanciamo una pietra verso l'alto. Sappiamo che quando toccherà il suolo avrà acquisito una velocità di 50 m/s. Si chiede: quanto tempo la pietra resterà in aria?
Come al solito, chi vuole tentare di risolverlo da solo si fermi qui
Utilizziamo lo schema di Fig. 2
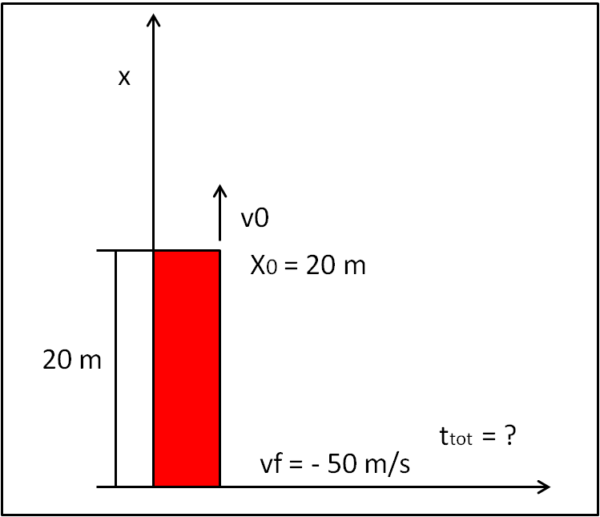
A prima vista sembrerebbe di avere un numero insufficiente di dati, ma, riflettendoci sopra, la faccenda si chiarisce in fretta. E' vero che non conosciamo la velocità iniziale, ma possiamo descrivere completamente il moto attraverso la legge oraria e attraverso la formula che lega velocità e accelerazione. In tal modo otteniamo due equazioni in due incognite: v0 e ttot.
Poniamo l'asse delle x diretto verso l'alto con origine al suolo. In tal modo la velocità finale vf deve essere presa con il segno meno. La legge oraria ci dice che:
xf = x0 + vo ttot - 1/2 g ttot2 .... (1)
inoltre abbiamo che:
vf = v0 - gttot .... (2)
Inseriamo i dati conosciuti...
x0 = 20 m
xf = 0 m
g = 9.8 m/s2
vf = -50 m/s
Le (1) e (2) diventano
0 = 20 + vo ttot - (9.8/2)ttot2
(9.8/2)ttot2 - vottot - 20 = 0 .... (1bis)
- 50 = v0 - 9.8 ttot
vo = 9.8 ttot - 50 .... (2bis)
Inseriamo nella (1bis) il valore di v0 ricavato dalla (2bis)
(9.8/2)ttot2 - (9.8 ttot - 50)ttot - 20 = 0
4.9 ttot2 - 9.8ttot2 + 50 ttot - 20 = 0
4.9 ttot2 - 50ttot + 20 = 0
ttot1 = 0.42 s
ttot2 = 9.79 s
La prima soluzione è da scartare in quanto porterebbe a una velocità iniziale negativa, ossia rivolta vero il basso
v0 = 9.8 0.42 - 50 = - 45.88 m/s
il che è impossibile perché la pietra è stata lanciata verso l'alto, ossia la sua velocità deve essere positiva
La soluzione è quindi
ttot = 9.79 s
che corrisponde a una velocità iniziale:
v0 = 9.8 9.79 - 50 = 45.94 m/s





