Scopriamo i mille volti della geometria **
Bastano due circonferenze e un triangolo per impostare un problema non certo difficile, ma che può essere risolto in vari modi. Poche regole geometriche bastano per dare il via alla fantasia e alla deduzione. Credete a me, in questo mondo ormai abituato a chiedere e a ricevere la pappa pronta (senza nemmeno verificare se viene detta la verità), un po' di sana geometria può fare solo bene.
Eccoci, allora, a un problema per il quale vengono fornite CINQUE diverse soluzioni che permettono di rinfrescare la memoria a molti e insegnare a qualcuno.
Consideriamo due semi-circonferenze che si incrociano tra loro come mostra la Fig. 1

Siano O e O' i loro centri. Dal punto d'intersezione delle circonferenze tracciamo i segmenti che toccano l'estremità più vicina delle due circonferenze. Essi formano un angolo θ. Lo scopo dell'esercizio è determinare il valore di questo angolo, conoscendo qualche distanza tra vari punti delle due circonferenze.
In particolare:
DB = 8
BC = 4
CE = 12
Chi vuol provare da solo, può fermarsi qui ...
Primo metodo (basato sulla bisettrice)
Tracciamo AD e AO in Fig. 2

Possiamo dedurre facilmente che DC = 16 e OE = 8. OE è il raggio della circonferenza di destra, per cui anche AO = 8.
Consideriamo i due triangoli individuati dai lati azzurro e rosso (DAO e CAO). Essi sono simili in quanto hanno un angolo in comune e una coppia di lati proporzionali. La Fig. 3 mostra meglio questi due triangoli e la loro similitudine.
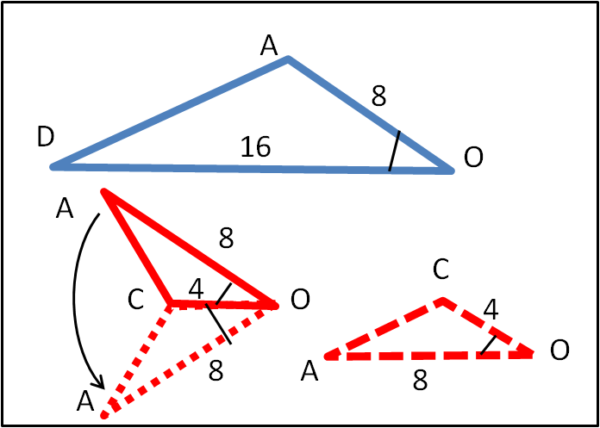
Sappiamo che AB/DB = OC/AO = 1/2
Dalla similitudine deve anche essere:
CA/DA = 1/2
Sappiamo, però, che:
DB/DC = 4/8 = 1/2
Consideriamo il triangolo DAC.
Il rapporto 1/2 tra i suoi due lati CA e DA è uguale al rapporto tra i due segmenti (DB e DC) individuati da AB sul terzo lato DC del triangolo. Questa situazione non può non farci ricordare il teorema delle bisettrici, che dice proprio che la bisettrice di un angolo taglia il lato opposto in due parti che hanno lo stesso rapporto degli altri due lati. Ne segue che il segmento AB è bisettrice dell'angolo DAC. Il che vuol dire che BAC è la sua metà. Ma, l'angolo DAC è un angolo retto dato che è angolo alla circonferenza corrispondente a DC che è un diametro. Ne segue che:
BAC = 45
Per completezza riportiamo anche la dimostrazione del teorema della bisettrice.
Consideriamo il triangolo ABC della Fig. 4.
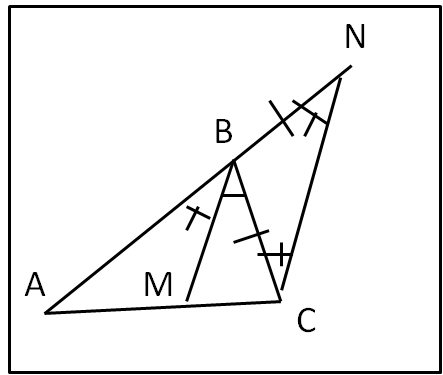
BM sia la bisettrice di ABC, Dal punto C tracciamo la parallela a BM fino a incontrare il prolungamento di AB in N. Per il ben noto teorema di Talete:
AB/BN = AM/MC .... (1)
ABM = BNC
Ma
ABM= MBC
e
MBC = BCN
ossia:
ABM = BCN
Ne segue che BNC è un triangolo isoscele, in quanto BNC = BCN
Il che vuol dire che
BN = BC
La proporzione (1) diventa
AB/BC = AM/MC
c.v.d.
Secondo metodo (basato solo sugli angoli)
Risolviamo il nostro problema, lavorando praticamente solo con gli angoli. Inseriamo la Fig. 5
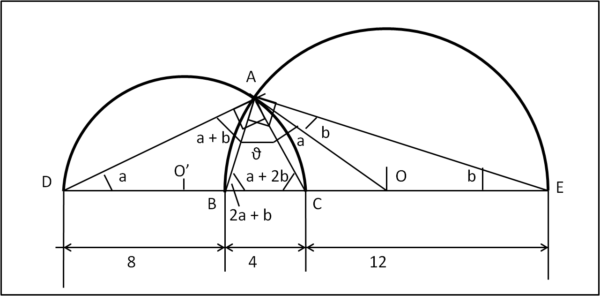
Riproponiamo, come fatto precedentemente, i triangoli simili DAO e CAO. Essendo simili deve valere che
CAO = ADB = a .... (2)
Il triangolo OAE è isoscele avendo, come lati, due raggi della circonferenza grande . Ne segue che:
OAC = OEA = b
Consideriamo il triangolo rettangolo DAC, dove:
DAB = 90 - θ
Dal triangolo rettangolo BAC abbiamo che:
CAE = 90 - θ
Ne segue che
DAB = CAE
Ma CAE = a + b e quindi deve essere uguale ad a + b anche l'angolo DAB
DAB = a + b .... (3)
Passiamo al triangolo BAC.
L'angolo ABC (angolo esterno del triangolo DAB) deve essere uguale alla somma degli altri due angoli di DAB, ossia:
ABC = ADB + DAB
Dalla (2) e dalla (3)
ABC = a + (a + b) = 2a + b
Dal triangolo CAE abbiamo che il suo angolo esterno ACB deve valere:
ACB = (a +b) + b = a + 2b
Ricordiamo che
CAE = 90 - θ
ossia:
(a + b) = 90 - θ .... (4)
Sommiamo gli angoli del triangolo BAC
(2a + b) + (a + 2b) + θ = 180
3a + 3b + θ = 180
3(a + b) +θ = 180
Ricordando la (4), possiamo scrivere:
3(90 - θ) + θ = 180
270 - 2θ = 180
2θ = 90
θ = 45
Terzo metodo (basato sulle tangenti e gli angoli alla circonferenza)
Inseriamo la Fig. 6
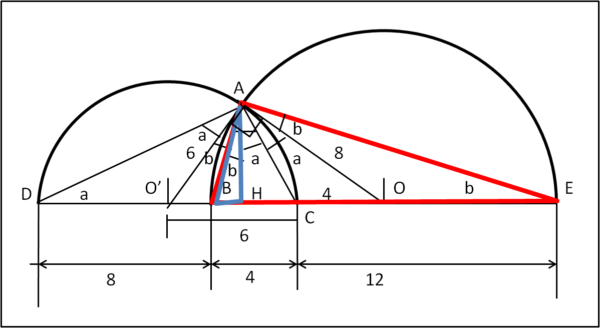
Cominciamo col manipolare un pochino le misure iniziali:
DC = 8 + 4 = 12
O'D (raggio cerchio piccolo) = 6
O'O = 6 + 4 = 10
O'O2 = 100
O'A = 6
O'A2 = 36
OA = 8
OA2 = 64
Ne segue che il quadrato di O'O (100) è uguale alla somma dei quadrati di O'A e OA (36 + 64). Se ne deduce che il triangolo O'AO è un triangolo rettangolo in A.
Questo risultato ci dice anche che O'A è tangente alla circonferenza grande in A e che OA è tangente alla circonferenza piccola in A.
Consideriamo l'arco AC della circonferenza piccola. L'angolo alla circonferenza ADC lo chiamiamo a. Sappiamo che tutti gli angoli alla circonferenza sono uguali tra loro e, nel caso limite (D = A), abbiamo che CAO = a. Per meglio comprendere questa configurazione limite, inseriamo la Fig. 7.
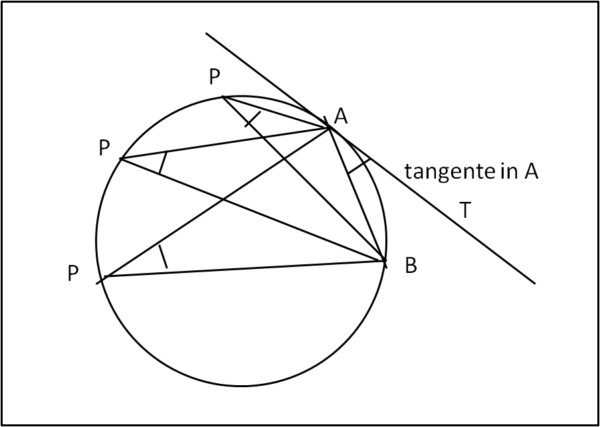
L'arco sia AC. Facendo variare P sulla circonferenza l'angolo BPA è sempre uguale. Nel caso limite in cui P coincida con A, l'angolo BAT vale proprio BPA.
Torniamo alla Fig. 6.
Per quanto appena detto possiamo scrivere:
CAO = a
e, analogamente per l'arco AB del cerchio grande, si ha
O'AB = b
I triangoli DAO' e OAE sono isosceli (due lati sono raggi delle rispettive circonferenze), per cui:
DAO' = a
OAE = b
Tracciamo AH perpendicolare a OO' e consideriamo i triangoli AHB (azzurro) e BAR (rosso). Essi sono simili in quanto entrambi rettangoli e con un angolo in comune (ABE). Ne segue che anche il terzo angolo deve essere uguale, ossia:
BAH = b
Per le stesse caratteristiche anche i triangoli AHC e DAC sono simili, per cui:
HAC = a
Consideriamo l'angolo O'AO. Esso è retto, come dimostrato precedentemente, per cui:
b + b + a + a = 90
2a + 2b = 90
a + b = 90/2 = 45
Ma
a + b = θ
per cui:
θ = 45
Quarto metodo (basato su un solo angolo)
Introduciamo la Fig. 8
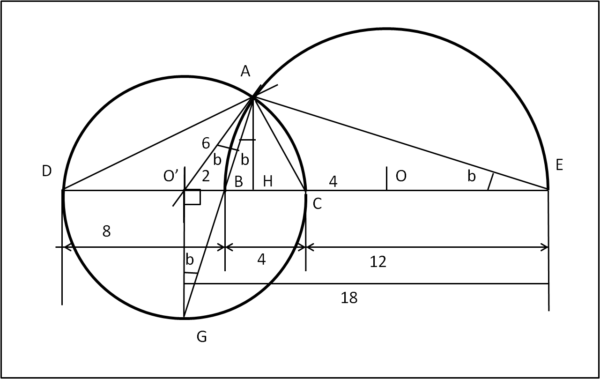
Innanzitutto, determiniamo il valore di O'B = 2 e poi costruiamo il cerchio piccolo per intero. Prolunghiamo AB fino a incontrare la sua circonferenza in G. Notiamo che NON sappiamo ancora come sia inclinato il segmento O'G.
Consideriamo i triangoli AO'B e O'AE. Essi sono simili in quanto hanno l'angolo AO'E in comune e inoltre vale la proporzione tra i lati:
O'B/O'A =O'A/O'E = 2/8 = 6/18 = 1/3
Ne segue che l'angolo AEO' è uguale all'angolo O'AB e lo possiamo chiamare b.
Il triangolo AO'G è isoscele (due lati sono raggi) e, quindi:
O'GA = O'AG = b
Ma anche i triangoli BAE e HAE sono simili, dato che sono rettangoli e hanno l'angolo ABE in comune. Ne segue che:
BAH = AEB = b
Considerando che
O'GA = BAH = b
Ne segue che i segmenti AH e O'G sono paralleli e, quindi, anche l'angolo OG'B deve essere retto.
Non ci resta che considerare l'arco GC della circonferenza piccola. Ricordiamo che l'angolo al centro è doppio dell'angolo alla circonferenza, per cui:
G'OC = 2 GAC = 2θ = 90
θ = 45
Quinto metodo (un pizzico di trigonometria)
Inseriamo la Fig. 9
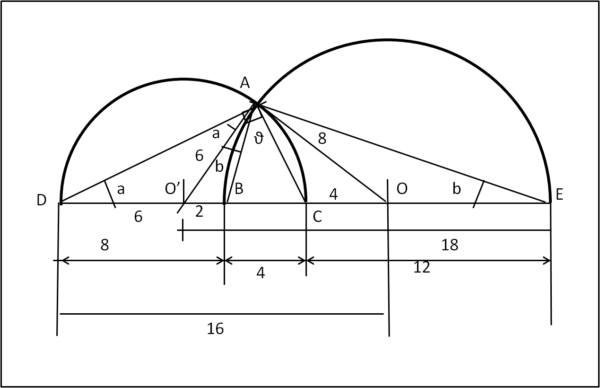
I triangoli DAO e CAO sono simili dato che hanno un angolo in comune e i lati in proporzione
OC/OA = OA/OD = 1/2
Deve, perciò, anche essere:
AC/AD = 1/2
Il che vuole anche dire che
tan a = 1/2
I triangoli O'AE e O'AB sono anch'essi simili dato che hanno un angolo in comune e i lati in proporzione:
O'B/O'A = O'A/O'E = 1/3
e, quindi:
tan b = 1/3
Non è difficile calcolare la tangente di (a + b)...
tan (a + b) = (tan a + tan b)/(1 - tana tan b) = (1/2 + 1/3)/( 1 - 1/2 · 1/3)
tan (a + b) = (5/6)/(1 - 1/6) = 5/6/(5/6) = 1
ma ciò vuol dire che
a + b = 45
Ne segue che
θ = 90 - (a + b) = 90 - 45
θ = 45
Sicuramente esistono altri metodi, magari anche più veloci dell'ultimo proposto. Perché non provare a trovarli? I due cerchi che si intersecano non hanno più segreti!






4 commenti
Nonostante che io non sia un matematico e malapena usi la trigonometria per lavoro, questo esercizio sono riuscito a comprenderlo! Grazie Vincenzo!!
che piacere Lamberto!
Un problema carino.
Non so se sia molto diverso da quelli proposti (magari anche solo nella forma) .
vi sottopongo anche questa via
La soluzione precedente si basa su due fatti: il teorema della tangente e secante e il teorema della bisettrice.
La seguente usa solo un principio di similitudine (ovviamente i due procedimenti sono equivalenti e "sotto-sotto" sono la stessa "cosa").