Categorie: Matematica
Tags: infinito iperbole logaritmo di due serie armonica
Scritto da: Vincenzo Zappalà
Commenti:1
Un paradosso ... "infinito" ***
Conosciamo bene il concetto di "infinito", gioia e dolore di tutti i matematici. Appare a volta come una saponetta che sembra di avere bloccato e invece ti sfugge via in un battibaleno. Da un lato appare qualcosa senza alcuna fine, dall'altro sembra una quantità quantificabile. Abbiamo usato il concetto di limite per cercare di dominarlo, ma l'infinito ha sempre in serbo qualche sorpresa.
Questo articolo vuole presentare e risolvere uno dei tanti paradossi legati all'infinito e lo fa aiutandosi con una semplice rappresentazione geometrica.
Il paradosso che andiamo a descrivere, può essere sintetizzato nell'espressione che segue:
n - n ≠ 0
Una disuguaglianza IMPOSSIBILE, ma altri non è che è uno dei soliti "scherzi" che può inventarsi l'infinito quando viene maneggiato con poca attenzione.
Iniziamo considerando due serie armoniche, tra le più "imbarazzanti".
Prendiamo prima la più semplice:
1 + 1/2 + 1/3 + 1/4 + 1/5 + ...
Essa sembrerebbe tendere a un valore finito (aggiungo sempre un valore più piccolo) e, invece, è una serie divergente che tende proprio a infinito.
Prendiamone un'altra un po' più complicata:
1 - 1/2 + 1/3 - 1/4 + 1/5 - 1/6 + .... ....(1)
Sembra proprio saltellare attorno allo zero e sembrerebbe proprio che il suo valore sia ZERO.
Vediamo di dimostrarlo
Scriviamo i termini negativi in modo leggermente diverso:
- 1/2 = 1/2 - 2/2 = 1/2 - 1
- 1/4 = 1/4 - 2/4 = 1/4 - 1/2
-1/6 = 1/6 - 2/6 = 1/6 - 1/3
e via dicendo...
Andiamo a inserire questi valori al posto dei termini negativi della (1)
1 + (1/2 - 1) + 1/3 + (1/4 - 1/2) + 1/5 + (1/6 - 1/3) + .... .... (2)
Eliminiamo pure le parentesi
1 + 1/2 - 1 + 1/3 + 1/4 - 1/2 + 1/5 + 1/6 - 1/3 + ....
Separiamo la nostra serie in due serie, una con i termini positivi e una con i termini negativi ...
1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + ...
- 1 - 1/2 - 1/3 - ....
Entrambe queste serie hanno INFINITI termini. La loro somma è sicuramente uguale alla serie di partenza, ossia la (1). Non ci resta che sommarle, mettendo in evidenza il segno meno nella seconda.
1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + ...
- (1 + 1/2 + 1/3 + ....)
La serie rossa e la serie blu dentro la parentesi sono decisamente uguali ed entrambe estese fino all'infinito. Ne segue che il risultato della somma non può che essere ZERO.
Perfetto? Purtroppo NO! La serie (1) non vale assolutamente ZERO come previsto, ma ha un valore finito e, in particolare, è uguale a ln 2. Ma cosa c'entra il logaritmo naturale di 2? In poche parole, sommando tra loro due serie identiche, ma di segno contrario, entrambe estese all'infinito otteniamo uno strano numero che tutto è fuori che ZERO. Verrebbe subito da pensare che un infinito sia "diverso" dall'altro... In altre parole:
infinito - infinito ≠ 0
Sappiamo che, in realtà, questa relazione ha una sua ragione, ma non vogliamo complicare troppo le cose e limitiamoci a dimostrare che, in realtà, il valore ln 2 è proprio quello GIUSTO!
Lasciamo da parte la matematica e vediamo di risolvere il paradosso per via puramente geometrica.
Riprendiamo la serie sotto la forma indicata nella (2)
1 + (1/2 - 1) + 1/3 + (1/4 - 1/2) + 1/5 + (1/6 - 1/3) + 1/7 + ....
Abbiamo sicuramente a che fare con termini del tipo 1/k e non possiamo non pensare all'iperbole equilatera di equazione y = 1/x
Disegniamo la Fig. 1.
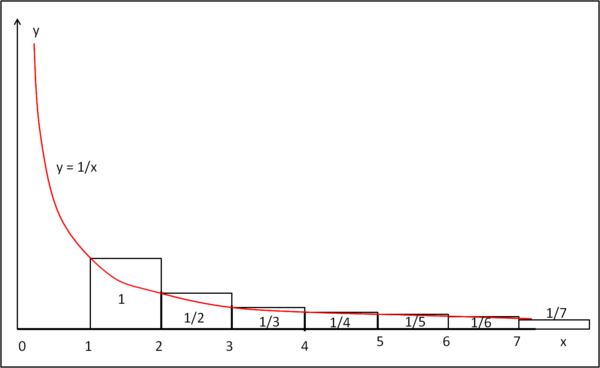
Il punto con x = 1 ha come ordinata y = 1. Il punto con x = 2 ha come ordinata y = 1/2 e via dicendo. Costruiamo tanti rettangolini di base uguali a 1 e altezza uguale all'ordinata del vertice in basso a destra (1/x).
Ogni rettangolino ha area uguale a 1/x, con x che vale 1, 2, 3, 4, ...
Ripetiamo la figura precedente nella nuova Fig. 2, dove abbiamo solo inserito la nostra serie.
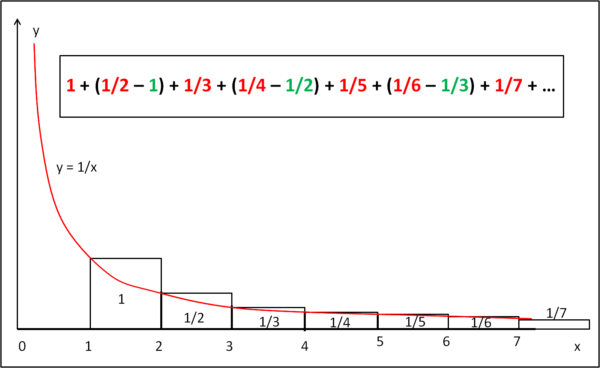
Notiamo subito che i termini positivi rossi corrispondono esattamente alle aree dei rettangolini costruiti sull'iperbole.
Bene cominciamo a prendere i termini della serie e rappresentarli con i rettangolini, nella Fig. 3.
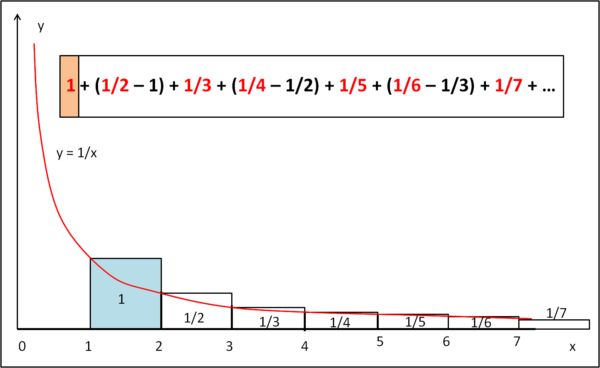
Il primo termine è UNO e quindi corrisponde al primo rettangolino che è , in realtà, un quadrato di area 1.
In Fig. 4, consideriamo i termini della serie segnati in rosa.
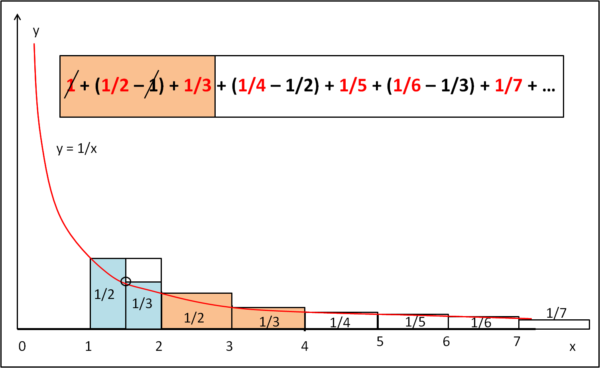
A cosa corrispondono ? Beh, basta fare la somma: 1 si elimina con - 1 e restano quindi due aree da rappresentare, quelle segnate in rosa nel grafico, ossia 1/2 e 1/3. Adesso facciamo un semplice giochino... le comprimiamo, dividendole per due e le inseriamo nel quadratino di lato 1. Per compensare il restringimento dobbiamo aumentare la loro altezza (y) di un fattore due e l'area dei due rettangolini rosa diventano l'area di quelli azzurri. In altre parole, la somma dei termini in rosa della serie sono rappresentati dalle due aree azzurre.
Passiamo alla Fig. 5, dove allunghiamo i termini della serie che vengono analizzati.
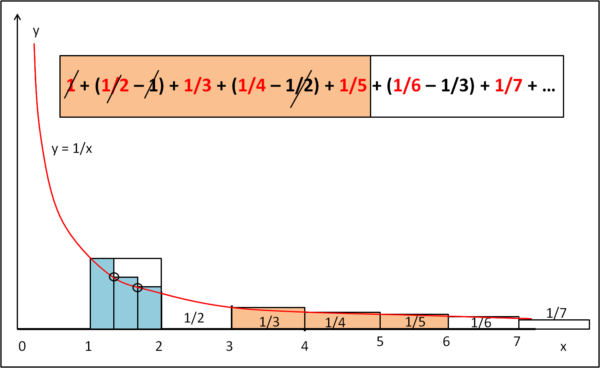
Notiamo che facendo la somma dei termini in rosa, oltre a eliminare 1, si elimina anche 1/2. Le aree descritte dalla serie sono adesso soltanto i termini 1/3, 1/4 e 1/5. Eseguiamo l'operazione già svolta precedentemente. Dividiamo la base di questi rettangoli per 3 e li portiamo nel quadratino di lato 1. Per compensare la riduzione di un fattore 3, basta moltiplicare l'altezza dei rettangolini azzurri per 3, ottenendo9 quelli rappresentati in figura. Le tre aree azzurre sono proprio l'area descritta dai termini in rosa della serie.
Notiamo una cosa importantissima, che avremmo già dovuto notare nel caso precedente: i vertici in alto a sinistra di ogni rettangolino azzurro stanno proprio sulla curva y = 1/x. Il "perché" è ovvio, dato che abbiamo costruito questi rettangolini attraverso una contrazione del valore della x e un successivo allungamento del valore della y. Non ci può sfuggire il fatto che operando in questo modo le aree azzurre, che rappresentano la serie prendendo sempre più termini, continuano ad avvicinarsi all'area che sta sotto la nostra iperbole.
Come ulteriore prova, consideriamo la Fig. 6, dove abbiamo preso ancora più termini della serie.
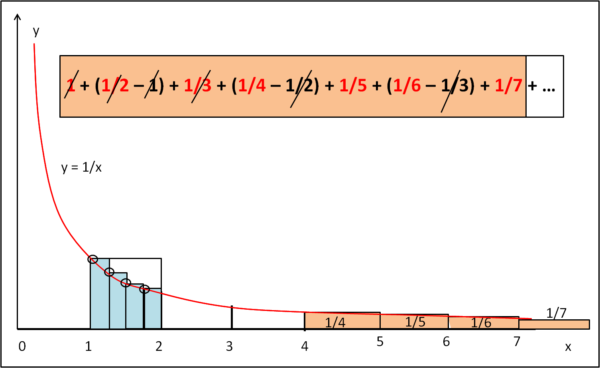
Questa volta sparisce anche l'area relativa a 1/3 e rimangono le aree relative ai rettangolini di area 1/4, 1/5, 1/6 e 1/7. Solita operazione, dividendo la base per 4 e moltiplicando l'altezza per 4. I nuovi rettangolini azzurri approssimano ancora meglio l'area che sta sotto l'iperbole.
E' inutile proseguire... abbiamo capito benissimo che prendendo sempre più termini della serie, ossia spingendoci su una sua rappresentazione più "completa", otteniamo una sempre migliore approssimazione dell'area sotto l'iperbole, limitata all'intervallo tra 1 e 2. Andando all'infinito la somma delle aree azzurre diventa proprio l'area sotto l'iperbole, come mostra la Fig. 7.
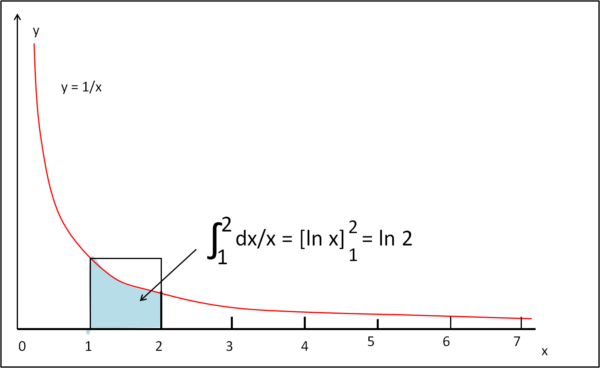
Una somma che contenga infiniti termini può essere descritta da un integrale delimitato tra i due valori estremi dell'intervallo di integrazione. Cosa dobbiamo integrare? Beh, è ovvio: l'iperbole, in modo da ottenere l'area che sta sotto di essa.
La nostra serie equivale perciò all'area della parte azzurra che può essere espressa come:
∫21 (1/x) dx = [ln x]21 = ln 2 - ln 1 = ln 2
Una serie infinita, che sembra potersi dividere in due serie identiche, entrambe infinite, dà come risultato proprio quello strano numero, del tutto inaspettato (a prima vista).≠
Noi possiamo fermarci qui, ma quanto abbiamo descritto può portare molto più in là fino a scrivere e rappresentare un valore sempre più approssimato del "solito", immancabile, π. Basta cambiare un poco (?!) i termini della serie.
Lo avevo detto... Attenzione agli scherzi dell'ambiguo e sfuggevole INFINITO!






1 commento
Con la tua dimostrazione che il risultato sia ln2 è incredibilmente chiaro. Non mi è chiaro invece a cosa ti riferisci quando scrivi:
infinito - infinito ≠ 0. Sappiamo che, in realtà, questa relazione ha una sua ragione, ma non vogliamo complicare troppo le cose
Inoltre, assaggiato lo zuccherino, ora non puoi - secondo me - nemmeno astenerti dal portarci molto più in là fino a scrivere e rappresentare un valore sempre più approssimato del "solito", immancabile, π. Visto che basta cambiare un poco (?!) i termini della serie.