Tutti gli articoli della serie "Con la testa tra le nuvole" sono disponibili QUI

Nel precedente articolo abbiamo visto che il vapore acqueo puro è molto improbabile che condensi fino a formare le goccioline contenute nelle nubi. La formazione delle goccioline è ostacolata dalla loro tensione superficiale.

Le nubi comunque in natura si formano. È evidente che c’è un meccanismo che aiuta a superare l’ostacolo posto dalla tensione superficiale.
L’aiuto viene dalla alcune particelle sospese nell’aria che nell’insieme sono denominate aerosol atmosferico.

In questo articolo vedremo come queste particelle con il vapore acqueo nell’aria possono formare embrioni di goccioline che hanno la possibilità di continuare a crescere fino a raggiungere le dimensioni delle goccioline delle nuvole. Concentreremo l’attenzione sulle particelle solubili nell’acqua che sono le più efficaci nella creazione di embrioni di goccioline. Vedremo come si modifica l’equazione di Kelvin per la presenza di un soluto nelle goccioline. Le curve che risultano sono denominate curve di Köhler. Esamineremo queste curve per capire quali sono le condizioni che portano una gocciolina a crescere o che fermano la crescita della gocciolina.

~ ~ ~ ~

Vediamo l’effetto delle particelle di aerosol sulla condensazione

Nell’aria ci sono numerose particelle che nell’insieme sono denominate aerosol atmosferico. La quantità, le dimensioni e la composizione delle particelle che formano l'aerosol atmosferico è molto varia. Alcune di esse sono fatte di sostanze sostanze che repellono l’acqua, sostanze idrofobe. Sulla superficie delle sostanze idrofobe le goccioline d’acqua tendono a mantenere la forma sferica. Altre sono di sostanze che consentono all’acqua di distribuirsi sulla loro superficie. Queste sostanze sono chiamate idrofile. Alcune sostanze sono anche solubili nell’acqua. Nella figura c’è sotto una rappresentazione molto schematica dello spaccato di particelle dei tre tipi.

Le goccioline che si formano sulle particelle idrofobe rimangono delle dimensioni delle goccioline che si formano casualmente nell’aria, come se la particella non ci fosse.

Il vapore acqueo che si condensa sulle particelle totalmente idrofile si distribuisce sulla superficie della particella. Il raggio di curvatura dello strato di acqua è quello della particella. Se la particella è abbastanza grande, il raggio di curvatura può essere maggiore del raggio critico. Il raggio che consente alla gocciolina di crescere spontaneamente.

Questi sono i casi estremi, ci sono anche particelle parzialmente idrofile che hanno proprietà intermedie tra i due casi estremi delle particelle idrofobe e totalmente idrofile.

Se la particella è solubile nell’acqua, le molecole d’acqua vengono dapprima catturate dalla particella. Se l’umidità relativa è abbastanza elevata la quantità di molecole d’acqua catturate crescerà fino a formare una soluzione con la sostanza della particella. All’effetto sul raggio si aggiunge una riduzione la pressione di vapore di equilibrio oltre la quale è possibile la condensazione. La riduzione è dovuta all’inframezzarsi delle molecole della particella, il soluto, tra quelle dell’acqua.

~ ~ ~ ~

Esaminiamo la relazione tra la riduzione della pressione di vapore di equilibrio e raggio della gocciolina di soluzione

Nota: per non confondere i significati il termine “pressione di vapore saturo” viene normalmente riservato alla pressione di vapore di equilibrio con una superficie piana di acqua pura liquida. Per soluzioni e per le goccioline, anche di acqua pura, utilizzo il termine generico pressione di vapore di equilibrio.

La riduzione della pressione di vapore di equilibrio dipende dalle quantità di molecole d’acqua rispetto alle molecole totali o al numero di ioni totali .

Una possibile espressione di questa dipendenza è nota come legge di Raoult:

o mettendo in evidenza il fattore f:

Nella figura sotto vediamo in forma grafica la relazione di f con il raggio della gocciolina. La condensazione sulla gocciolina aggiunge acqua alla soluzione, mentre la quantità di sale rimane invariata al suo valore iniziale.

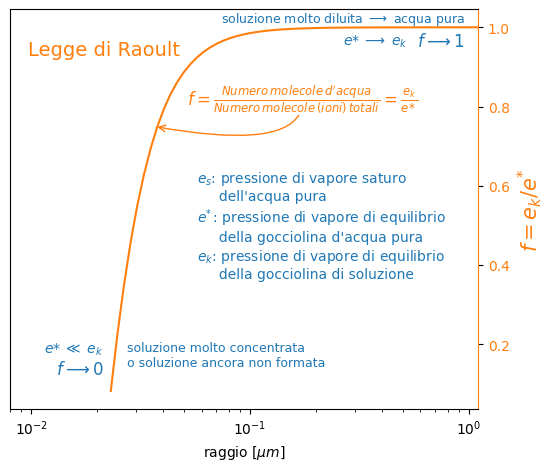
Quindi mano mano che la gocciolina cresce la soluzione si diluisce e tende sempre più a comportarsi come l’acqua pura. Vale a dire che la pressione di vapore sulla gocciolina tende a quella ricavabile dalla equazione di Kelvin vista nell’articolo precedente ed f tende a 1.

Per soluzioni molto concentrate la pressione di vapore di equilibro del vapore tende a quella sul sale puro, che è molto vicina allo 0. Quindi anche f tende a 0.

 

Molte soluzioni in natura non seguono la legge di Raoult, ma l’andamento qualitativo è simile.

~ ~ ~ ~

Utilizziamo l’umidità relativa di equilibrio anche per descrivere questa relazione

Poiché normalmente è possibile misurare l’umidità relativa è utile rappresentare il punto di equilibrio con l’umidità relativa di equilibrio che corrisponde al raggio della gocciolina, in modo simile alla equazione di Kelvin.

Ricordiamo che l’umidità relativa fa sempre riferimento alla pressione di vapore saturo e_s. Quindi l’umidità relativa che stiamo cercando è

UR_k = e_k / e_s,
dove e_k è le pressioni di vapore di equilibrio sulla soluzione.

Dalla legge di Raoult sappiamo che

f = e_k / e^*,

dove e^* è la pressioni di vapore di equilibrio su una gocciolina d’acqua pura.

L’equazione di Kelvin ci da l’umidità relativa di equilibrio UR^* = e^* / e_s per goccioline di acqua pura in funzione del loro raggio.

Possiamo concludere che l’umidità relativa di equilibrio su una gocciolina di soluzione si può ottenere moltiplicando il valore ottenuto con la legge di Kelvin per l’umidità relativa di una gocciolina di acqua pura delle stesse dimensioni per il fattore f:

Vediamo questa relazione in forma grafica.

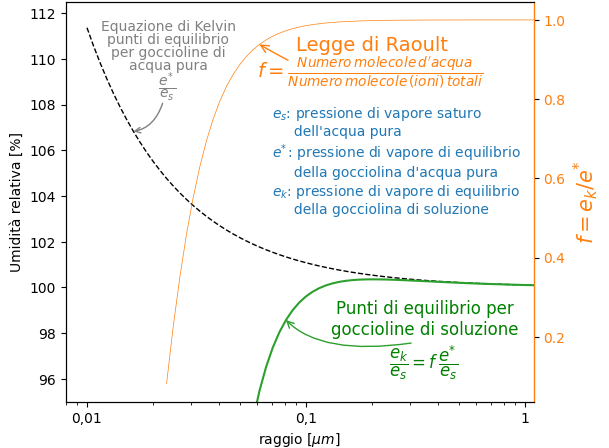
Per goccioline relativamente grandi, la quantità d’acqua è molto maggiore di quella del soluto, che rimane costante. Le caratteristiche dalla soluzione tendono a quelle dell’acqua pura. Quindi l’umidità relativa di equilibrio tende a quella stabilita dalla equazione di Kelvin.

All’estremo opposto, per goccioline piccole, la quantità di acqua è molto piccola. Di conseguenza f è molto piccolo. Quindi l’umidità relativa di equilibrio si riduce drasticamente.

Questo è certamente un vantaggio per la formazione delle goccioline poiché la condensazione può iniziare su queste goccioline per valori di umidità relativa anche inferiori alla saturazione, 100%.

Nel mezzo l’andamento del grafico non è apprezzabile con la scala utilizzata sopra. La zona che ci interessa è quella immediatamente sopra la saturazione. Per mettere in evidenza la parte di curva di interesse, si utilizza spesso una scala ingrandita per questa zona.

Nella figura sotto sono rappresentate due curve dell’umidità relativa di equilibrio in funzione del raggio della gocciolina per goccioline che nascono da piccoli nuclei di NaCl.  Il diverso andamento delle due curve è dovuto alla diversa massa del nucleo iniziale.

Curve di questo tipo sono chiamate curve di Köhler. Le curve rappresentano l’umidità relativa di equilibrio. Valori di umidità relativa dell’ambiente superiori all’umidità relativa di equilibrio consentono alla gocciolina di crescere. Valori inferiori tendono a far evaporare la gocciolina.

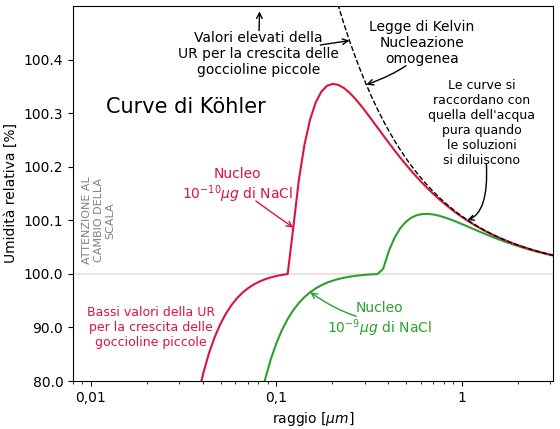
La situazione è nettamente più favorevole alla crescita delle goccioline rispetto alla nucleazione omogenea. Cioè alla crescita a partire da nuclei di acqua pura. Nell’articolo precedente abbiamo visto che l’umidità relativa necessaria per la crescita della gocciolina con la nucleazione omogenea è rappresentata dalla curva di Kelvin. Nella figura è la curva tratteggiata. Questa curva ci indica che sono necessari valori molto elevati di umidità relativa per consentire la crescita di goccioline piccole. Valori che normalmente non sono presenti nelle nubi. Quindi le piccole goccioline formate dalla aggregazione casuale di molecole di vapore tendono ad evaporare.

Invece quando la gocciolina cresce a partire da un nucleo di una sostanza solubile, come il comune sale da cucina, la crescita delle goccioline può iniziare anche per livelli bassi di umidità relativa, anche sotto la saturazione UR<100%.

Per proseguire la crescita oltre il micron di raggio, occorre comunque una soprasaturazione dell’umidità nell’aria.

Nel grafico sotto vediamo cosa accade nelle situazioni descritte dalle due curva del grafico precedente quando il livello di umidità relativa nell’aria è del 100,2%, cioè una soprasarurazione dello 0,2%. Un livello che è maggiore del massimo di una delle curve ed inferiore del massimo dell’altra curva.

Le fecce rappresentano come si muove l’umidità relativa di equilibrio delle goccioline. Il livello di umidità relativa dell’ambiente è rappresentato dalla linea orizzontale celeste.

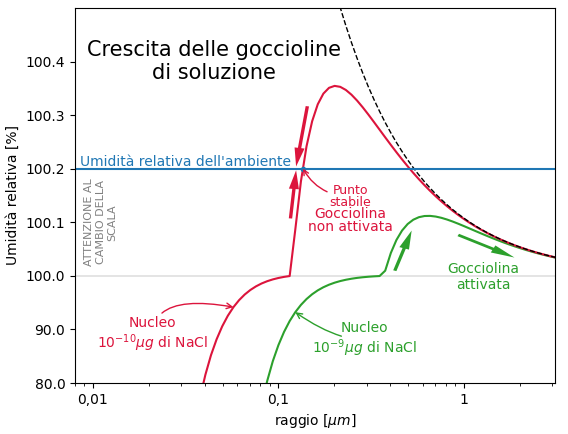
Ora seguiamo la curva rossa. La curva rappresenta i punti di equilibrio a partire da un nucleo di sale. Le goccioline possono crescere fino a che l’umidità relativa di equilibrio della gocciolina è minore della umidità relativa dell’ambiente.

Quando la gocciolina raggiunge la dimensione per la quale l’umidità relativa di equilibrio è uguale alla umidità relativa dell’ambiente, la crescita della gocciolina si ferma. La gocciolina si trova in una situazione di equilibrio stabile. Se dovesse crescere l’umidità relativa di equilibrio diverrebbe superiore a quella dell’ambiente e la gocciolina inizierebbe ad evaporare fino a tornare nella situazione di equilibrio. Se dovesse ridursi, la sua umidità di equilibrio scenderebbe sotto l’umidità relativa dell’ambiente e la gocciolina tornerebbe a crescere fino a ritornare nella situazione di equilibrio.

Quindi la crescita della gocciolina si ferma a queste dimensioni. La gocciolina non raggiunge le dimensioni delle goccioline che formano le nubi. La gocciolina è detta non attivata. Goccioline di queste dimensioni contribuiscono alla foschia.

Ora seguiamo la curva verde. Questa curva è sempre sotto il livello di saturazione dell’ambiente. Le goccioline che si formano a partire da nuclei rappresentati da questa curva apparentemente non trovano ostacoli alla crescita. La gocciolina viene detta attivata.

Nei prossimi articoli vedremo fino a che punto e in quale modo la condensazione del vapore può far crescere queste goccioline fino alla dimensioni tipiche di una gocciolina all'interno di una nuvola (r ≈10µm) e se le può far crescere ulteriormente fino a raggiungere le dimensioni delle gocce di pioggia (r ≈1mm).