In questo articolo parleremo di decadimento radioattivo o -se preferite- dell'interazione nucleare debole. Niente di veramente nuovo per il circolo che ha già trattato questo argomento sia in modo divulgativo dai "papallicoli" sia in modo un po' più articolato (QUI). Tuttavia, Esso si sposa molto bene anche a quanto abbiamo detto dell'interazione forte e al suo gioco di tira e molla tra i protoni messi in gabbia all'interno del nucleo.

La volta scorsa abbiamo visto come sia impresa non facile mantenere unito un nucleo atomico in cui regna continua la lotta tra repulsione e attrazione. Abbiamo, però, anche accennato all'aiuto insostituibile dei neutroni che con la loro presenza e la loro indifferenza verso la forza elettrostatica riescono a mantenere un equilibrio più o meno duraturo nel nucleo atomico. Se il nucleo è poco affollato, i protoni sono praticamente a contatto e non hanno bisogno di un grande aiuto, ma se il nucleo ha troppi protoni essi raggiungono distanze reciproche che possono far vincere l'interazione repulsiva e rendere critica la sopravvivenza del nucleo. A questo punto i neutroni sono fondamentali perché si inseriscono tra protoni relativamente lontani e li attraggono a sé interrompendo la repulsione coulombiana . A tutto, però c'è un limite... Se i protoni diventano eccessivamente numerosi (83 per l'esattezza), i neutroni non riescono a fare miracoli e il nucleo è costretto a decadere espellendo sia protoni che neutroni (decadimento alfa). Veniamo, perciò, al punto che vogliamo investigare meglio: quale deve essere il rapporto tra protoni e neutroni che permetta la maggiore stabilità?

Possiamo disegnare un grafico  che mostra quanto ci stiamo chiedendo e nel frattempo dimostri l'azione dei vari decadimenti radioattivi.

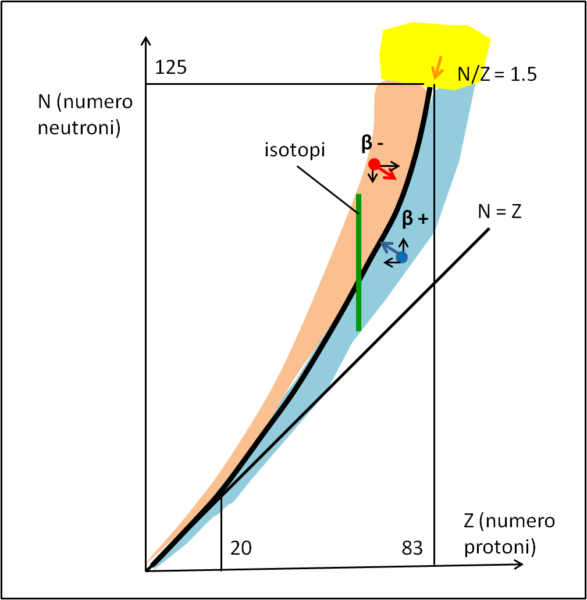
L'asse delle ordinate riporta il numero di neutroni e quello delle ascisse il numero di protoni. La stabilità è facile da individuare fino a nuclei che abbiano 20 protoni. Essa segue perfettamente la linea a 45°, ossia il numero di neutroni è uguale al numero di protoni.

Dopo questo tratto praticamente rettilineo i neutroni devono intervenire più severamente ed aumentare rispetto ai protoni. La linea di stabilità si sposta verso sinistra e il rapporto tra neutroni e protoni arriva fino a 1.5. Questo valore corrisponde a un nucleo con 83 protoni dove l'instabilità diventa la norma e scatta il decadimento alfa. Ma torniamo all'inizio del nostro grafico...

Sappiamo benissimo che un nucleo atomico può ammettere vari isotopi, i quali possono essere più meno stabili. Dato un certo numero di protoni questo vuol dire che si possono trovare nuclei che stanno sia al di sopra che al di sotto della linea di stabilità.

Consideriamo quelli che si piazzano nella parte a sinistra della linea di stabilità. Essi rappresentano isotopi instabili per eccesso di neutroni. Cosa succede, allora, al nucleo X rappresentato dalla pallina rossa ? Esso deve cercare di riportarsi sulla linea, ossia seguire la direzione e il verso riportato dal vettore rosso. Come può fare? Semplice si può spostare sulla destra,  guadagnando un protone e scendere verso il basso, perdendo un neutrone. Se Z è il numero di protoni (numero atomico) e N è il numero di neutroni, basta che un neutrone diventi un protone e il gioco è fatto...

Il nostro nucleo X ha Z protoni e A nucleoni (numero di massa, uguale alla somma di neutroni e protoni):

^A_ZX

Se trasformo un neutrone in protone, il numero di massa A rimane lo stesso (il numero di nucleoni non cambia), il numero di neutroni N scende di uno e il numero atomico Z sale di uno. Si ottiene un nuovo elemento il cui nucleo può essere indicato con:

^A_{(Z + 1)} Y

Il rapporto tra N e Z diventa

(N-1)/(Z+ 1) < N/Z

Il nuovo nucleo si è riportato sulla linea di stabilità. Il processo appena descritto non è altri che il decadimento β-.

Facciamo un esempio pratico...

Prendiamo il "celebre" carbonio 14, notoriamente instabile e utilissimo nella datazione dei fossili, proprio per il suo decadimento.

¹⁴₆C

Esso perde un neutrone che si trasforma in protone, ossia diventa

¹⁴₇N

che è il nucleo dell'azoto 14

Se calcoliamo il rapporto Z/A nei due casi, abbiamo:

prima del decadimento: 8/6 = 1.3        per il carbonio

dopo il decadimento: 7/7 = 1.0        per l'azoto.

Il decadimento beta ha riportato il nucleo di carbonio 14 sulla linea di stabilità trasformandolo in azoto 14. Ovviamente, nella reazione "scappa" via un elettrone direttamente dal nucleo. In parole povere, il neutrone non ha carica, ma se si trasforma in protone diventa positivo e libera un elettrone  negativo.

Poniamoci, adesso, nella parte destra del grafico, sotto la linea di stabilità. Questa volta il nucleo deve avvicinarsi alla linea da destra. La strada migliore è trasformare un protone in neutrone, in modo da diminuire il numero atomico e aumentare il numero dei neutroni. In questo processo deve scappare qualcosa di positivo, affinché il protone perda la sua carica. Si ha quindi l'emissione di un positrone. Ma vediamo cosa succede al nucleo.

Z diminuisce di uno, mentre aumenta di uno il numero N di neutroni. Il numero di massa rimane, ovviamente, immutato.

^A_ZX

^A(_{Z - 1)}Y

Il rapporto tra neutroni e protoni diventa:

(N + 1)/(Z - 1) > N/Z

Il nuovo nucleo si è portato nuovamente verso la linea di stabilità. Facciamo, anche in questo caso, un esempio pratico:

Consideriamo il rame 64:

⁶⁴₂₉ Cu

N/Z = 35/29 = 1.21

Attivando la trasformazione otteniamo:

⁶⁴₂₈Ni

(N + 1)/(Z - 1 )= 36/28 = 1.29

Da cui l'avvicinamento alla linea di stabilità.

Tutto ciò riesce a capitare fino a che il numero atomico resta inferiore a 83. Per valori più alti il nucleo è ormai troppo affollato e il valore N/Z supera 1.5. Per ottenere stabilità bisogna scendere verso il basso e avvicinarsi a 1.5. Il taglio di particelle deve essere più drastico e si ottiene espellendo un particella alfa che altri non è che il nucleo dell'elio 4, ossia ⁴₂He. Ne segue che il rapporto N/Z diventa:

(N - 2)/(Z - 2)

Ciò comporta una discesa verso il valore 1.5. La faccenda, però, non è così semplice. Facciamo un esempio con l'uranio 238.

²³⁸₉₂ U

N/Z = 146/92 = 1.59

Espelliamo la particella alfa e otteniamo

²³⁴₉₀Th

(N - 2)/(Z - 2)= 144/90 = 1.60

Accidenti! E' aumentato il rapporto invece di diminuire... Nessun problema, a questo punto sfruttiamo il decadimento β^- trasformando il torio 234 in protoattinio 234, ossia:

²³⁴91Pa

che comporta

(N - 1)/(Z + 1) = 143/91 = 1.57

Tuttavia, quando abbiamo a che fare con elementi troppo pesanti i nuclei sono altamente instabili e i decadimenti piuttosto frequenti... In ogni modo, la perdita di protoni diminuisce il numero atomico e porta il nucleo verso valori che si avvicinano alla stabilità.

Insomma, cercando la stabilità abbiamo avuto a che fare con i decadimenti.