Ritorniamo sull’integrale indefinito, definendolo ancora meglio. Ne approfittiamo per dimostrare formalmente il teorema fondamentale (facoltativo…).

Definiamo meglio l’integrale indefinito, ossia l’integrale che serve per poter calcolare gli integrali definiti.

Abbiamo visto che una funzione F(x) è detta primitiva di f(x) quando la sua derivata è uguale a f(x). Ossia:

F ’(x) = f(x)

Proviamo a calcolare qualche primitiva…

f(x) = 2x

F(x) = primitiva (2x) = x²

Infatti:

d(x²)/dx = 2x

f(x) = sen(x)

F(x) = - cos(x)

Infatti:

d(- cos(x))/dx = sen (x)

f(x) = 1/x

F(x) = ln(x)

Infatti:

d(ln(x))/dx = 1/x

E via dicendo…

Siamo sicuri di aver scritto qualcosa di veramente corretto? Beh, non proprio…

Prendiamo il primo caso:

f(x) = 2x

Proviamo a scegliere un’altra primitiva, sempre che esista… Sì che esiste, ad esempio:

F(x) = x² + 5

Infatti:

d(x² + 5)/dx = 2x

E la stessa cosa succederebbe per le altre funzioni…

Ma, allora, vi sono infinite primitive di una funzione!  Ciò dipende dal fatto molto semplice che la derivata di una costante è sempre ZERO.

Possiamo perciò dire:

se F(x) è una primitiva della funzione f(x), lo sono anche tutte le G(x) = F(x) + c, con c costante arbitraria. Esse sono tutte “curve” che differiscono soltanto per uno spostamento lungo l’asse delle y, come mostrato in Fig. 1.

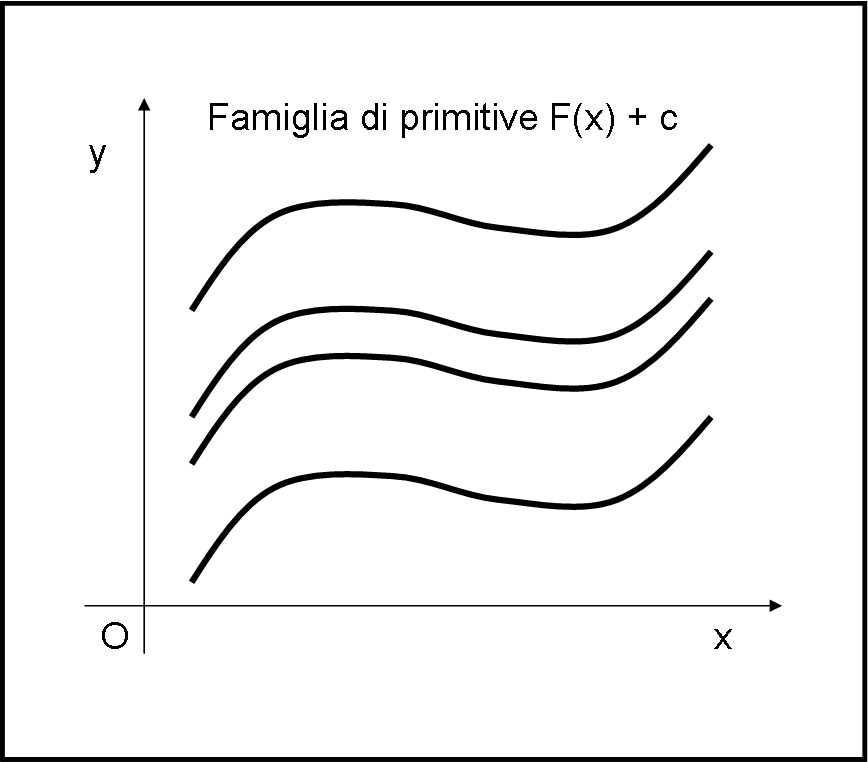
Si chiama integrale indefinito di una certa funzione f(x) l’insieme di tutte le sue primitive, ossia di tutte le funzioni F(x) che abbiano come derivata f(x). Le curve di Fig. 1 hanno, infatti, tutte la stessa derivata e poco conta che siano spostate verso l’alto o verso il basso.

L’integrale indefinito si indica con il simbolo:

∫ f(x) dx

Esso non è più un valore numerico, come l’integrale definito, ma è una vera e propria funzione od operazione, proprio l’inverso della derivata.

Applicando la definizione alla funzione y = 2x (ad esempio), possiamo scrivere:

∫ 2x dx = x² + c

O alla funzione f(x) = 1/x

∫ 1/x dx = ln(x) + c

E così via…

N.B: la parte, in corsivo, che segue (e che implica i tre asterischi dell’articolo) è piuttosto complicata concettualmente (magari, invece, mi spavento per niente...) e non veramente necessaria. Tuttavia, mi sembrava doveroso riportare anche la dimostrazione formale del teorema fondamentale del calcolo integrale o di Torricelli-Ballow. Ormai ci sembra una banalità, ma senza di lui non sarebbe stato possibile il passaggio da integrale indefinito a integrale definito.

Sia f(x) una funzione continua in un certo intervallo (a,b).

Prima di iniziare, ricordiamo che l’integrale della funzione tra due valori a e b non è altro che un numero che indica l’area compresa tra la funzione e l’asse delle x. Il che vuole anche dire che non dipende assolutamente da x, ma solo dalla funzione e dagli estremi a e b. Ragione per cui l’integrale si può scrivere … come si vuole, ossia:

∫_a^b f(x)dx = ∫_a^b f(u)du = ∫_a^b f(s)ds … ecc., ecc.

Adesso, però, noi vogliamo costruire un integrale definito che sia funzione della x, facendo variare quest’ultima tra a e b. Scegliamo, quindi, una x qualsiasi compresa tra a e b e consideriamo l’integrale definito

∫_a^x f(u)du

Al variare di x l’integrale definito precedente varia e diventa esso stesso una funzione di x. Chiamiamola funzione integrale F(x). Come si nota, abbiamo preso una u qualsiasi dato che l’integrale così definito è adesso funzione di f, di a e anche di x che prende il posto di a e può variare lungo l’intervallo. Per ogni x, però, l’integrale diventa un numero. E’ quindi più che logico scegliere una “u” e non inserire nuovamente la “x” all’interno dell’integrale, dato che creerebbe un’inutile confusione: una x che varia tra a e se stessa… no, meglio scegliere una u qualsiasi, tanto, alla fine, si ottiene sempre e comunque un numero che dipende dalla x variabile.

F(x) = ∫_a^x f(u)du

Notiamo, in particolare, che:

F(a) = ∫_a^a f(u)du = 0

e

F(b) = ∫_a^b f(u)du

Il teorema fondamentale recita esattamente:

Se y = f(x) è una funzione continua nell’intervallo (a,b), allora la funzione integrale F(x) = ∫_a^x f(u)du è derivabile e risulta F’(x) = f(x), cioè F(x) è una primitiva di f(x). Notiamo che F(x) rappresenta l’area compresa tra a e x, per definizione di integrale definito.

Questo è un classico teorema matematico che sembra dire una cosa ovvia (noi in pratica l’abbiamo già dedotta in modo un po’ semplificato), ma che deve essere formalmente dimostrato per potere essere applicato, sempre e comunque.

Consideriamo un intervallino (x, x+h) con h molto piccolo.

Abbiamo:

F(x) = ∫_a^x f(u)du

e

F(x + h) = ∫_a^x+h f(u)du

Ovviamente, possiamo scrivere:

F(x + h) - F(x) = ∫_a^x+h f(u)du - ∫_a^x f(u)du = ∫_a^x f(u)du + ∫_x^x+h f(u)du - ∫_a^x f(u)du = ∫_x^x+h f(u)du    …. (1)

Notate che abbiamo usato una proprietà degli integrali definiti…

Ne usiamo subito un’altra, quella definita dal teorema della media (ricordate?)

∫_x^x+h f(u)du = f(c)(x + h – x) = f(c)h

Con c compresso tra x e x+h. La (1) diventa:

F(x + h) - F(x) = f(c)h

(F(x + h) - F(x))/h = f(c)

Non ci resta che passare al limite per h che tende a zero.

lim _h→0  (F(x + h) - F(x))/h = lim _h→0 f(c) = f(x)   …. (2)

Se h tende a zero la c deve per forza coincidere con x…

Scriviamo di nuovo la (2):

lim _h→0  (F(x + h) - F(x))/h  = f(x)

Il primo membro, però, non è altro che la derivate di F(x), ossia:

F’(x) = f(x)

Come volevasi dimostrare.

Cosa ci ha detto, in pratica, questo teorema? Una cosa fondamentale: la derivata della funzione “area” F(x) è proprio la funzione f(x). Il legame tra definizione analitica e geometrica è stato trovato e dimostrato. Sappiamo come calcolare gli integrali definiti!

A questo punto, risulta, infatti, banale scrivere che se F(x) è una primitiva, esistono infinite altre funzioni primitive che differiscono per una costante. Sia, per esempio, F(x) + c.

F(x) = ∫_a^x f(u) du

E quindi:

∫_a^x f(u) du  = F(x) + c

Ma anche:

∫_a^a f(u) du = F(a) + c = 0

Da cui c = - F(a)

E, infine:

∫_a^x f(u) du  = F(x) + c = F(x) – F(a)

∫_a^b f(u) du  = F(b) – F(a)

In breve: si calcola dapprima una primitiva qualsiasi F(x) di f (x). Il valore dell’integrale definito è dato dalla differenza tra il valore che tale primitiva assume nel punto b e il valore che essa assume nel punto a. A questo punto possiamo benissimo inserire nuovamente la x nell’integrale, dato che siamo di fronte a un numero e la x non crea più confusione:

∫_a^b f(x) dx  = F(b) – F(a)

Per coloro che non hanno letto la parte precedente, in corsivo, ripetiamo l’enunciato del teorema fondamentale:

Se y = f(x) è una funzione continua nell’intervallo (a,b), allora la funzione integrale F(x) = ∫_a^x f(u) du è derivabile e risulta F’(x) = f(x), cioè F(x) è una primitiva di f(x). Il valore dell’integrale definito sarà dato dalla differenza tra il valore che tale primitiva assume nel punto b e il valore che essa assume nel punto a.

Non ci resta, adesso, che riassumere e fare qualche esempio…

 

QUI il capitolo precedente

QUI il capitolo successivo

QUI l'intero corso di matematica