Categorie: Matematica
Tags: geometria quadrato quiz settore circolare
Scritto da: Vincenzo Zappalà
Commenti:6
(Q) Un solo passaggio con Pitagora (con soluzione)**
Più che un quiz questo esercizio e poco più di uno scherzo. Dato un settore circolare pari a un quarto di un cerchio, inseriamo al suo interno un quadrato, come mostra la figura che segue.
Quanto vale l'area del quadrato in funzione del raggio r ?
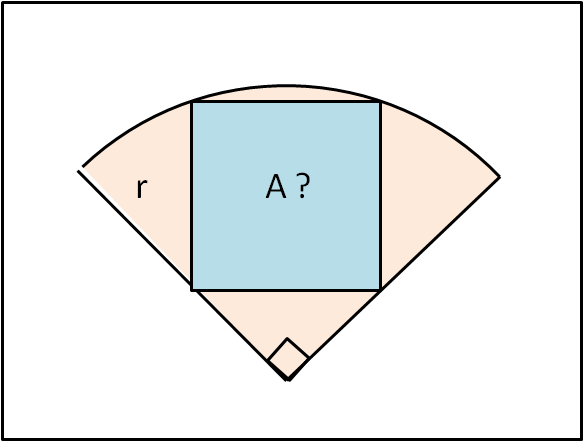
La soluzione più rapida ha bisogno di applicare una sola volta il teorema di Pitagora e di un po' di fantasia. Mi raccomando Andy... non essere troppo veloce (chissà mai che ...). Al limite scrivi solo il risultato finale senza spiegazione.
SOLUZIONE
Oltre alle soluzioni di Andy e Leandro (la più rapida), riportate nei commenti, vi offro la mia, per la quale basta guardare la figura qua sotto:
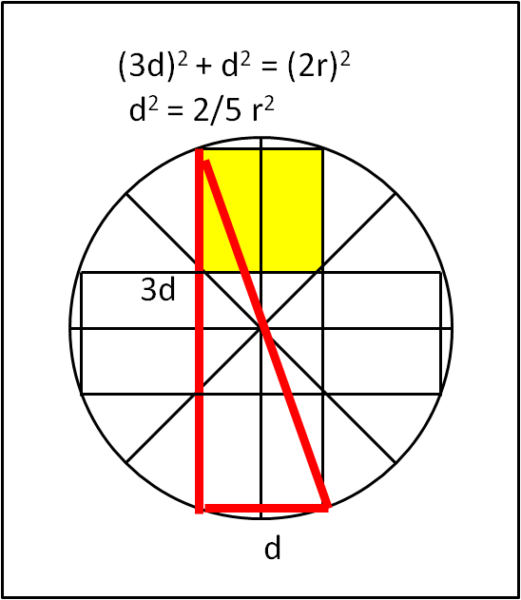
Ovviamente tutti i quadrati sono uguali per ovvia simmetria e il triangolo rosso è rettangolo perché inscritto in una semicirconferenza...






6 commenti
Una rappresentazione "pentagrammatica" o "aurea" del disegno.... :
:
ma anche in modo più semplice...
da cui
quindi Area=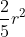
ottimo Andy ! Io ho usato ancora un altro metodo, ma questo è il più rapido e semplice sicuramente. Basta, infatti, dimostrare che il cateto minore è la metà del lato del quadrato, ma questo è ovvio dato che gli angoli sono 45°
Possibile che sia risultato così difficile per gli altri? La geometria sembra una materia più ostica di quanto pensassi...
In realtà la soluzione corretta l'ha fornita Leandro.
Io avevo stimato l'angolo al centro Θ che sottende l'arco di corda L pari al lato del quadrato, di 36°.
Un errore di sottostima di poco meno di 9/10 di grado, poiché il valore corretto dell'angolo e:
36°52'11.63''
Accidenti! Scusami Leandro... ero convinto avesse risposto Andy.