(Q) L'area di un rettangolo (con soluzione) *
L'introduzione dello Jacobiano ci ha mostrato ancora una volta quanto sia importante la geometria per descrivere esaurientemente le formule matematiche e la loro applicazione pratica. Continuo, perciò, nei quiz geometrici sperando che le basi fondamentali si stabilizzino sempre di più.
Il quiz è veramente semplice e può essere risolto scrivendo una sola formula, sempre che vi ricordiate alcune proprietà geometriche che abbiamo già trattato... Mi scuso con Andy &Co., per la semplicità del quiz, ma sono impegnato nell'analisi degli integrali doppi quasi a tempo pieno. Accontentatevi...
Consideriamo un rettangolo ABCD, come mostrato nella figura che segue:
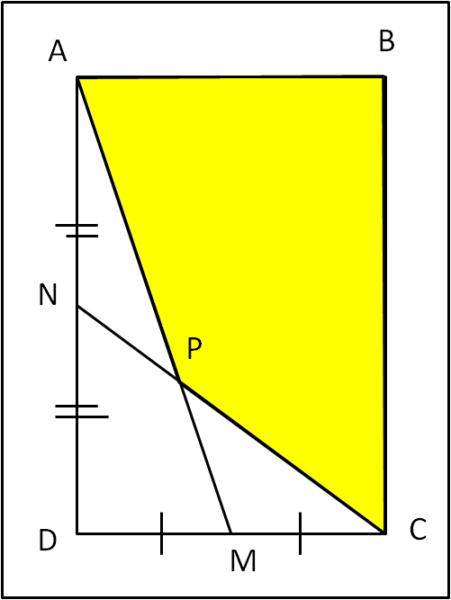
M e N sono i punti medi dei lati DC e AD. Congiungiamo A con M e C con N. Essi si incontrano in P.
Conoscendo l'area del quadrilatero ABCP sapreste dirmi rapidamente quanto vale l'area dell'intero rettangolo?
SOLUZIONE
Guardate i commenti di Andy e Leandro e il gioco è fatto!
Oppure, in modo equivalente, basta scrivere immediatamente che l'area gialla Ag
Ag = Atot/2 + Atot/12 + Atot/12
da cui Atot con un solo passaggio






7 commenti
Una volta e mezza l'area del quadrilatero giallo....
a parte il nostro Andy, c'è qualcuno che sa dirmi perché la risposta è giusta! Sono proprio un illuso...
Un'immagine dice tutto....
Metodo alternativo :
Le aree dei triangoli ADM e DCN sono uguali ad 1/4 dell'area totale.
Quindi l'area totale sarebbe 4 volte l'area di un triangolo.
Ovvero 2 volte l'area bianca più il quadrilatero NPDC
che si sovrappone.
Ma guarda caso esso è simile all'Areagialla , quindi la sua area vale esattamente
Areagialla / 4 , essendo i lati corrispondenti 1/2 di quelli del rettangolo.
Allora AreaTotale = 2 x ( Areabianca + Areagialla /4) .
da cui, poiché Areabianca = AreaTotale - Areagialla ,
AreaTotale = (2-1/2) Areagialla = 3/2 Areagialla
Per costruzione il punto P è il baricentro (intersezione mediane) del triangolo ACD. Pertanto ACD (la metà del rettangolo) è composto da 6 traingolini congruenti. Quindi ABCP è equivalente a 8 di questi triangolini, mentre tutto il rettangolo a 12. Il rapporto tra i due quadrilateri è 3/2.
Sia B' il simmetrico di B rispetto ad M. CM e BD due mediane di BCB' si tagliano in parti che stanno come 2:1.
Pertanto BCP è il doppio di DCP come PAB è il doppio di PAD. Quindi ABCP è il doppio di APCD.
Da cui (ABCP)/(ABCD)=2/3
Siano M' ed N' i punti medi di AB e BC rispettivamente e sia P' l'intersezione tra AN' e CM'.
Da P' si traccia la parallela a BC che incontra PC in N" e la parallela a CD che incontra PA in M".
Considerando i vari parallelogrammi costruiti, si ricava che ABCP è composto da due copie di AM'P', P'M'BN' ed N'P'C, mentre il rettangolo e composto da tre copie di queste figure.