I nostri amici Rocco e sprmnt2 hanno dato delle soluzioni al problema, ma, come spesso capita nei commenti, diventa un po' complicato saltare di commento in commento. Preferisco inserire un'ulteriore dimostrazione utilizzando molte figure e seguendo passo passo ogni azione. Le conoscenze necessarie sono veramente elementari, per cui chiunque può seguirle senza alcun problema...

Il procedimento assomiglia a quello di sprmnt2, ma è forse più immediata la visione geometrica. Il procedimento di Rocco sfrutta la riflessione della luce ed è sicuramente elegante.  Consideriamo in Fig. 1, a sinistra, il nostro triangolo QPR, colorato in rosa (a sinistra). Immaginiamo, adesso, di farne due copie identiche. Le due copie le ruotiamo attorno al lato PQ, in modo da portare Q in Q'. Una di queste copie la ruotiamo nuovamente attorno a PQ' in modo da portare R in R', ottenendo la figura di destra, quella su cui vogliamo lavorare.

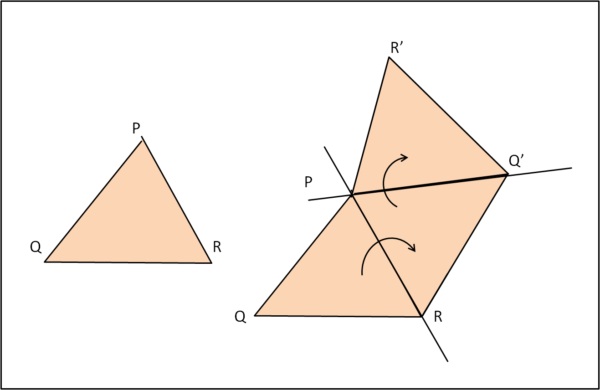
In Fig. 2, disegniamo un triangolo qualsiasi ABC i cui vertici tocchino i tre lati del triangolo QPR. Questo è il triangolo inscritto di cui vogliamo ottenere il perimetro minimo.

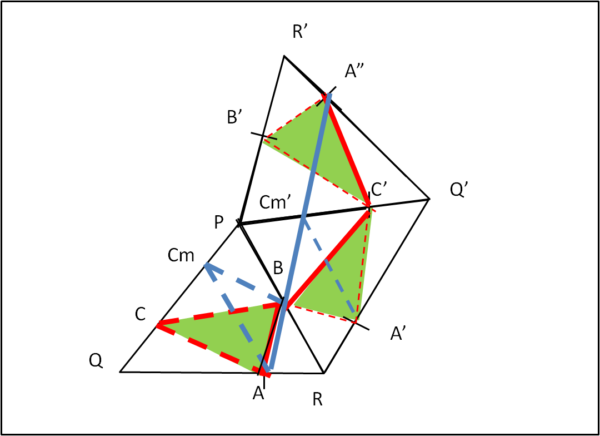
Come fatto precedentemente ruotiamo anche il triangolo ABC insieme con il triangolo PQR, ottenendo il triangolo verde ABC nei due ribaltamenti (BA'C' e C'A"B'). I tre segmenti rossi più spessi e continui rappresentano proprio i tre lati originali del triangolo ABC (AB, BC'=BC e C'A" = AC). In altre parole la linea spezzata ABC'A" determina graficamente il perimetro che vogliamo rendere minimo.

Sappiamo tutti molto bene che, nello spazio euclideo, la linea di lunghezza minore che collega due punti è la linea retta. Nel caso in esame A e A" dovrebbero perciò essere congiunti da una linea retta per potere rappresentare il perimetro minore, ossia seguire la linea azzurra AA". Ne consegue che il triangolo ABC non ha sicuramente le caratteristiche richieste. Mantenendo fisso A, la linea azzurra è quella che determinerebbe i punti B e C capaci di rendere minimo il perimetro. Basta prendere Cm al posto di C...

Non abbiamo ancora ottenuto ciò che volevamo, dato che il risultato vale solo per una certa posizione di A. Cambiandola cambia anche il perimetro dei triangoli inscritti corrispondenti. Però, però... vediamo prima la Fig. 3.

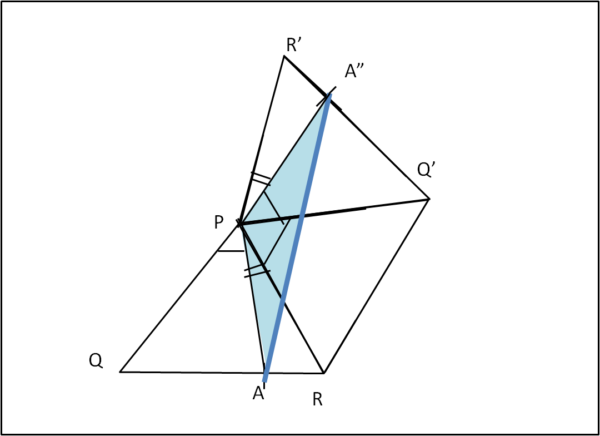
Consideriamo il triangolo PAA". Questo è un triangolo isoscele, dato che per costruzione PA è uguale a PA". L'angolo APA" vale esattamente il doppio dell'angolo QPR.

Infatti:

APA" = APR + RPQ' + Q'PA"

Ma

APR + Q'PA" = QPR

Così come

RPQ' = RPQ

Da cui

APA" = 2 RPQ

L'angolo RPQ rimane sempre lo stesso e non dipende dal punto A.

La Fig. 4 illustra il caso in cui il triangolo inscritto sia, ad esempio, AiBiCi (in verde).

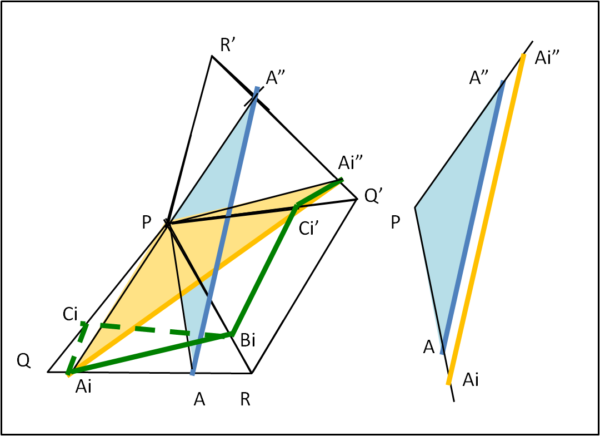
Ho indicato come indice un qualsiasi i, dato che A può essere un qualunque punto del lato QR così come Bi e Ci. E' facile costruire la linea spezzata relativa (verde continua) e la distanza minima AiAi" (in arancione). Per quanto appena dimostrato il triangolo arancione, corrispondente al minimo perimetro relativo ad AiBiCi, deve essere isoscele e avere lo stesso angolo in P del caso precedente.

Abbiamo di fronte una famiglia di triangoli isosceli con l'angolo tra i lati uguali che rimane sempre lo stesso. Tutti questi triangoli, che sono relativi ai perimetri minimi di ogni posizione di Ai, sono perciò SIMILI tra loro.  Il lato AiAi" può essere più o meno lungo, come viene mostrato nella parte destra della figura. Il triangolo inscritto di perimetro minimo è quello che ha il lato AiAi" minimo, dato che AiAi" è proprio il perimetro minimo per ogni punto Ai.

Affinché un triangolo isoscele simile a se stesso abbia il lato AiAi" minimo deve avere minimi anche i due lati uguali. Ossia, deve essere minimo il lato PAi = PAi". Ma,  quale può mai essere la distanza minima PAi ?

Facile rispondere: "Quella ottenuta tracciando la perpendicolare da P al lato QR". Questo segmento non è altro che l'altezza del triangolo che ha piede su QR.

Attenzione adesso! La scelta del vertice P nelle rotazioni iniziali non è certo vincolante. Avrei potuto scegliere gli altri due vertici, ottenendo lo stesso identico risultato. Ne segue che i punti B e C del triangolo di perimetro minimo devono anch'essi essere i piedi delle rispettive altezze.

La Fig. 5 mostra col contorno rosso il triangolo di minimo perimetro che volevamo ottenere.

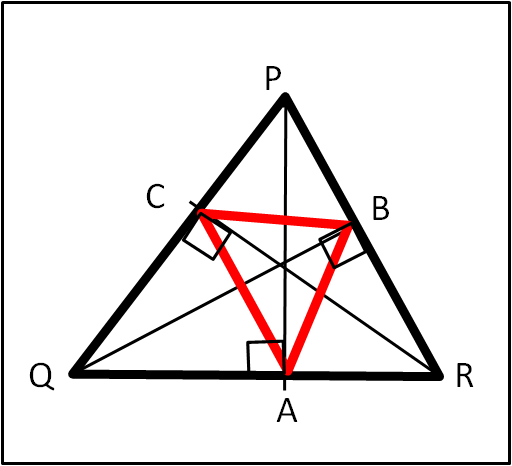
Il punto di incontro delle altezze è, ovviamente, l'ortocentro del triangolo QPR per cui non dobbiamo stupirci se il triangolo di minimo perimetro prende il nome di triangolo ortico. L'ideatore del problema, che ha avuto numerosi approcci, nei secoli seguenti  è stato Giovanni Fagnano che malgrado il significato di "fagnano" in piemontese (fannullone, pigro, indolente) ha invece svolto ottimi lavori in matematica.

Non è nemmeno difficile intuire successivi ampliamenti del problema, ma li lascio alla vostra immaginazione.

Un esempio di applicazione pratica? Scelto un punto A si potrebbe chiedere di costruire il tracciato, che colleghi i tre lati internamente, che sia quello più economico. Addirittura, si potrebbe subito costruire quello "più minimo dei minimi"...