Un mix di nozioni che vanno dalla rappresentazione geometrica di un binario ferroviario a quella “leggermente” più complicata di un Universo in espansione. In comune vi è un punto, che nel primo caso possiamo chiamare punto all’infinito, nell’altro caso Big Bang (anche se quest’ultimo si trova in una posizione temporale ben definita). Quest’articolo, un po’ strano, ci permette di capire meglio il piano ampliato e la natura di un punto singolare. Ci serve anche per vedere che eccezionale applicazione pratica viene fornita da una matematica a prima vista astratta e -forse- visionaria. Insomma, Alice è tornata tra di noi.

Sono piuttosto contento di questo articolo. Penso possa dare un aiuto sia per il viaggio nella matematica, che abbiamo appena iniziato, sia per dimostrare come essa non sia composta solo di pensieri astratti, ma di applicazioni oltremodo concrete. Di per sé la trattazione non è difficile, ma vi chiedo di leggerlo con molta attenzione, dato che i concetti base sono abbastanza sottili e parzialmente nascosti a una prima rapida lettura. Certe analogie non sono assolutamente casuali…

Consideriamolo come un’appendice delle “lezioni” di matematica. Ma anche un approccio ultra semplificato al Big Bang e alla sua ambigua natura. E’ un punto senza dimensione o qualche altra cosa? Non vi era lo spazio e nemmeno il tempo prima di lui e si fa in fretta ad andare in confusione. Anche perché il prima non poteva esistere… mamma mia! Cosa sia il Big Bang all’istante t = 0 è un concetto che mette spesso in imbarazzo (ma non solo voi!).

Purtroppo la fisica entra nel campo della MQ e si scontra con concetti che non sono solo difficili da descrivere, ma che sono spesso realmente sconosciuti. Come fare a definire in qualche modo questo punto iniziale che, comunque si chiami, può essere l’esatto opposto di se stesso? Spesso si liquida la faccenda dicendo che è un punto singolare. Ma se è un punto deve essere per definizione “singolare”, dato che non ha dimensioni (ne parleremo a lungo nelle prossime lezioni di matematica). Sì, però, è anche ovvio che non abbia dimensioni dato che lo spazio non esisteva ancora. Niente da fare… ragionando in termini fisici non ne usciamo vivi. Meno male che esiste la geometria e la matematica pronte a darci una mano.

Rotaie parallele e convergenti

Chiacchierando su rotaie, punti all’infinito, piani ampliati, siamo riusciti ad avere una certa idea di come sia facile cambiare la visione del mondo che ci circonda. Non per niente, abbiamo tranquillamente definito due rette parallele come due rette che non s’incontrano mai, ma anche l’esatto opposto, ossia due rette che hanno sempre un punto in comune, quello all’infinito. Non solo. Tutte le rette parallele tra loro hanno quel punto in comune.

Com’è stato possibile fare tutto ciò con una certa facilità, ossia considerare reale sia ciò che si può misurare con un metro (la distanza tra le rotaie) sia l’apparenza prospettica (la distanza che continua a decrescere)? E’ bastato giudicarle entrambe come realtà geometriche e matematiche, senza pensare a quale delle due fosse quella fisicamente “reale”. Insomma, abbiamo imparato ad accettare sia il mondo normale che quello del paese delle meraviglie di Alice. In fondo, già la MQ ci aveva aiutato in questa logica illogicità.

Torniamo, allora, alle nostre rotaie che ormai conosciamo molto bene. Consideriamo come realtà matematica e geometrica quella del piano ampliato, ossia assumiamo reale proprio l’asserzione che due rette parallele si incontrano sempre in un solo punto. Eseguendo questa piccola (ma ardua) operazione mentale (abbiamo attraversato il muro di Alice), possiamo tranquillamente parlare e disegnare punti all’infinito, rette parallele che si incontrano e traversine sempre uguali che continuano ad aumentare la loro lunghezza.

La Fig. 1 illustra questa configurazione in cui ci siamo coscientemente immersi e che non ci spaventa assolutamente più (almeno spero). Sappiamo che è una situazione apparente, una costruzione matematica, che, però, possiamo trattare con regole “normali”. Non dobbiamo, quindi, avere alcuna remora a disegnare un punto all’infinito. Da quel punto possiamo tracciare due rette che aumentano la loro distanza e considerarle a tutti gli effetti rette parallele. Sono o non sono rette che si incontrano in un punto all’infinito?  Non solo, però: anche altre rette più lontane sono sorelle “siamesi”. Ne potremmo disegnare a volontà, anche lontanissime tra di loro, in un certa posizione. Quale posizione? Beh… ad esempio, quella definita dalla retta T. Essa potrebbe essere quella in cui ci troviamo adesso e dove potremmo misurare facilmente la distanza “attuale” tra le rotaie. Sia essa, ad esempio, uguale a dn.

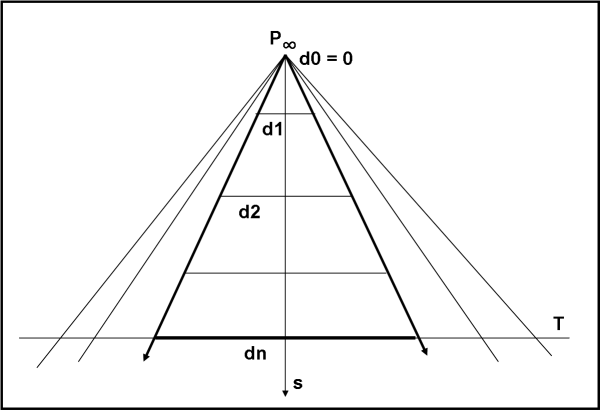
Avreste difficoltà a calcolare la distanza tra le rette parallele mentre si avvicinano al punto all’infinito P_∞? Direi proprio di no! Ovviamente, sempre e soltanto nell’ottica del nostro piano ampliato che stiamo considerando la realtà.

Come fare? Facilissimo, basta usare la Fig. 2.

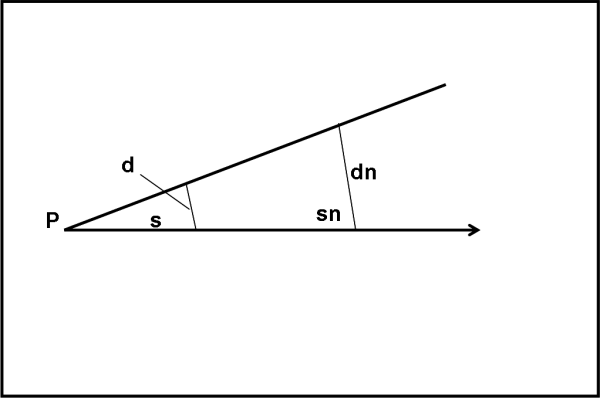
Conoscendo dn e la sua distanza sn dal punto P è immediato determinare la distanza d per ogni valore di s. Ne parleremo sicuramente nelle prossime lezioni di matematica, ma basta applicare le proprietà dei triangoli simili e fare una proporzione. Matematica e geometria veramente elementari.

dn : d = sn : s  

e quindi:

d =  (s dn)/ sn   = dn (s/sn)                          …. (1)

Fin qui, penso, che tutto sia banale (sempre che siate riusciti a entrare nel mondo di Alice e a considerare reale ciò che appare ai vostri occhi guardando la ferrovia andare verso l’orizzonte). Adesso, dobbiamo fare un passo che potrebbe sembrare un po’ più difficile. Suona strano chiamarlo così, dato che vuole dire soltanto rientrare nella stanza “normale” di Alice. Quando ci si abitua a vivere in una favola non è mai facile tornare nel mondo di tutti i giorni. Tuttavia, dobbiamo farlo e quindi seguitemi attentamente.

La (1) ci dice che è possibile moltiplicare la distanza misurata tra le traversine per un certo fattore o coefficiente o come preferite chiamarlo, per ottenere i valori di d. Questo coefficiente varia, ovviamente, al variare di s (vale, infatti, s/sn).

Torniamo alla realtà

Se possiamo fare questo, possiamo anche fare il viceversa. Ossia moltiplicare le lunghezze variabili tra le traversine per l’inverso di questo coefficiente di proporzionalità in modo da ridurle tutte alla stessa lunghezza.  In altre parole, conoscendo come varia la lunghezza delle traversine al variare di s, possiamo ricavare la lunghezza dn, che è poi quella “vera”. In pratica, usare la (1) al contrario.

Usare la (1) al contrario? Sembra una cosa da ridire, eppure ha un significato profondo. Vuol dire passare dal mondo del paese delle meraviglie a quello normale. Ottenere una lunghezza tra le traversine sempre costante, significa proprio dire che due rette parallele mantengono sempre la stessa distanza tra loro.

Non è certo difficile:

dn = (sn/s) d                      …. (2)

Data qualsiasi lunghezza misurata nel mondo apparente di Alice siamo in grado di ottenere sempre e comunque la stessa distanza dn, moltiplicando d per l’inverso del coefficiente di prima (ossia sn/s).

Vi assicuro che non ho detto cose complicate. Le ho solo volute esprimere in termini matematici. E’ un po’ come se avessi voluto portare tante cartine geografiche disegnate con scale diverse alle dimensioni reali. Pensateci un po’ sopra e vedrete che ho detto proprio una cosa banalissima che viene compiuta da tutti noi senza quasi pensarci.

In ogni modo, lavorando con un coefficiente di proporzionalità facilmente definibile siamo riusciti a ritornare nel mondo che consideriamo reale e che possiamo rappresentare nella Fig. 3. Per ogni distanza s abbiamo moltiplicato la relativa d per l’inverso del coefficiente e abbiamo sempre ottenuto la stessa dn. Le rotaie sono adesso sempre alla stessa distanza tra loro e le rette parallele non si incontrano mai…

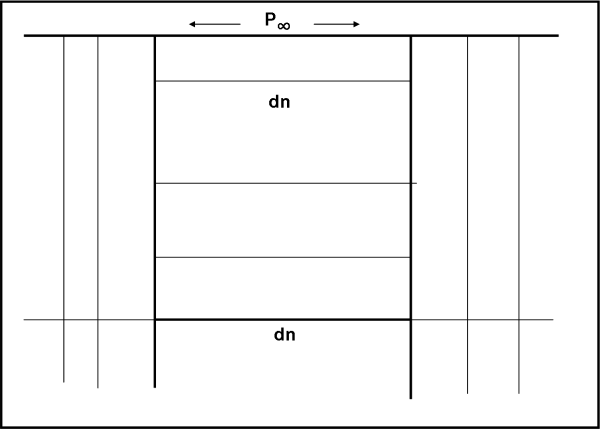
No, un momento, un momento. Anche se siamo passati in un mondo diverso non possiamo cancellare il mondo di prima. Anch’esso era reale! Le rette parallele non si incontrano mai, ma si incontrano comunque in un “punto” all’infinito. Come faccio a rendere compatibili queste due affermazioni completamente contrastanti? Basta assumere che il punto all’infinito diventi una linea di dimensioni enormi. Anzi, dato che posso disegnare infinite rette (intese come “tantissime”), anche molto distanti tra loro, che siano parallele, il punto all’infinito è diventato una linea sempre più lunga, ossia una linea di lunghezza … infinita. Posso ardire una definizione non proprio esatta, ma nemmeno troppo sbagliata: il punto all’infinito è un punto singolare. O -se preferite- molto strano, dato che può essere sia infinito che zero.

Attenzione: entrando sempre più nel mondo della matematica, ci si imbatterà in veri punti singolari, ma -in fondo- non differiscono concettualmente da questo.

Disegniamo il Big Bang

Avete visto? Abbiamo (più o meno facilmente) trasformato una realtà in un’altra. Ma -soprattutto- abbiamo trasformato un punto (all’infinito) in una retta (di lunghezza infinita per definizione di retta). Miracoli della geometria e della matematica. Poter dire le stesse cose attraverso la descrizione di un’entità fisica sarebbe stata un’impresa quasi assurda. Non per niente, la fisica usa il linguaggio della matematica!

Questo è stato, però, solo il preambolo che ci permetterà, tra poco, di capire l’ambiguità del Big Bang e considerarla come una ovvia conclusione matematica.

Riconosco di avere espresso concetti non semplicissimi. Per comprenderli appieno, ripeto ancora, bisogna riuscire a immedesimarsi in entrambe le realtà descritte: quella che ci circonda e quella apparente legata alla geometria proiettiva. Fatto questo, tutto diventa banale.

Spostiamoci quindi verso il Big Bang e verso l’espansione dello spazio. Abbiamo i mezzi per comprendere molto meglio la situazione e il modo di rappresentarla.

In tanti articoli che ho scritto (e anche nel Teatro del Cosmo), ho utilizzato la rappresentazione più “comune”, quella del palloncino che si gonfia. Ha tanti vantaggi “visivi”, ma ha anche tanti problemi costruttivi. La vediamo nella Fig. 4.

Al centro vi è il Big Bang, un punto geometrico. Da lui partono tutte le linee di Universo LU che si allontanano una dall’altra per effetto dell’espansione. E’ un po’ come se avessi disegnato al centro un punto all’infinito come quello di Fig. 1, con delle rette che più si allontanano da lui e più aumentano la distanza reciproca. Un vero e proprio gruppo infinito di rette parallele che partono dal loro punto all’infinito. Una rappresentazione molto utile perché ci fa vedere molto bene come le distanze tra le stelle (ognuna sulla propria linea di Universo) aumenti con il tempo. Tuttavia, la linea rossa curvilinea, che descrive il cono di luce passato di T (noi, ad esempio) ha una forma alquanto strana, che siamo riusciti a disegnare per punti, ma che non è certo un concetto troppo immediato. Le due linee più spesse UO permettono di definire, come al solito, i confini dell’Universo Osservabile al momento T. Anche queste non sono facili da disegnare perché bisognerebbe andare vicinissimi al punto all’infinito e tracciare le tangenti al cono di luce. Cosa non semplice, sicuramente.

Possiamo fare di meglio, per avvicinarci ancora di più alla Fig. 1 e alla rappresentazione del punto all’infinito (in questo caso il Big Bang) e di tutte le sue “rotaie” stellari? Proviamo con la Fig. 5.

Non ho fatto altro che “tagliare” le circonferenze (relative a un certo tempo t), che si allargano sempre più, e distenderle in modo che diventino delle rette.  Sì, adesso, il punto all’infinito BB assomiglia molto di più a quello della Fig.1 e anche le rotaie. Lo spazio, se non altro, non è più misurato lungo una circonferenza ma lungo una retta. Niente male.

Tuttavia, il cono di luce resta ancora una curva strana e la definizione geometrica delle rette che delimitano l’Universo Osservabile ha gli stessi problemi di prima. Questa rappresentazione (da un certo punto di vista più semplice) è quella che ho usato in Rosetta. Essa permette anche di stabilire “facilmente” il coefficiente per il quale bisogna moltiplicare la distanza tra due linee di Universo, oggi (in T), o -se preferite- tra due stelle, per calcolare la stessa distanza in tempi diversi da quello attuale. In fondo, siamo di fronte a due rette che convergono verso un solo punto, proprio come succedeva nella Fig. 1.

Anche se non è così semplice come appare, possiamo pensare nuovamente a triangoli simili che possiamo costruire andando verso il Big Bang. In altre parole, è relativamente facile calcolare le lunghezze delle “traversine spaziali”  a mano a mano che le rotaie-LU si avvicinano al Big Bang. Fidatevi, per adesso…

Vi prego di notare che quella che prima era la distanza rispetto al punto all’infinito è adesso diventata il tempo. Niente di speciale: abbiamo solo usato un’altra dimensione che ha lo stesso valore delle dimensioni spaziali (questo lo sappiamo ormai molto bene).  Assodata l’analogia quasi perfetta tra Fig. 1 e Fig. 5, siamo pronti per il passo conclusivo.

Immaginiamo di avere calcolato in qualche modo il coefficiente di proporzionalità che permette di passare dalla distanza tra le rotaie, a una certa distanza dal punto all’infinito (ossia, tra le linee di Universo delle stelle, ad un certo momento t), alle distanze tra le rotaie relative a qualsiasi altra distanza (tempo) dal punto all’infinito (Big Bang). Attraverso quel coefficiente (basta prenderne l’inverso, come fatto nella (2)) è anche possibile fare il viceversa, ossia passare a una figura equivalente alla Fig. 3, dove la distanza tra le rotaie sia rappresentata da una costante.

Come si chiama una distanza costante nel tempo che si riferisce ad una situazione in cui le rette sono tornate parallele tra loro? Un nome che già avete sentito… distanza comovente (chi vuole saperne di più può andare QUI o nel paragrafo relativo del Teatro del Cosmo). Cosa vuol dire in pratica? Poiché conosciamo la legge secondo la quale due rette parallele si avvicinano andando verso il Big Bang, possiamo cambiare il sistema descrittivo e disegnare tutte le linee di Universo parallele tra loro. Proprio come abbiamo fatto passando da Fig.1 a Fig. 3.

In questo contesto la distanza tra le stelle non dipende più dal tempo. Un grande vantaggio, anche perché per fare questo passaggio bisogna solo conoscere il famoso coefficiente di proporzionalità da utilizzare al contrario.

Un punto-retta o una retta-punto

Non vi è difficile capire che questo coefficiente dipende essenzialmente dall’espansione dell’Universo. Nel caso delle rette parallele che andavano “apparentemente” vero il punto all’infinito, la variazione di distanza era dovuta alla prospettiva, a una visione apparente che abbiamo considerato reale a tutti gli effetti; nel caso delle linee di Universo, invece, la variazione di distanza è proprio la realtà e descrive l’espansione dell’Universo. In parole povere, ciò che prima era stato un passaggio da una realtà apparente a una normale (da Fig. 1 a Fig. 3), adesso è diventato un passaggio da una realtà “normale” (espansione dell’Universo) a una apparente (distanza comovente, ossia annullamento apparente dell’espansione).

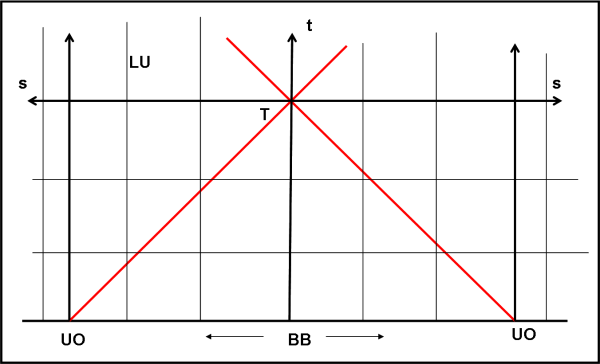
In quest’ultima rappresentazione, mostrata in Fig. 6, molte cose migliorano. Il cono di luce passato diventa proprio un triangolo (sul piano spazio-tempo del foglio). L’Universo Osservabile si misura direttamente come intersezione tra cono di luce passato e retta dello spazio al momento dell’invio della luce da parte delle stelle più lontane osservabili (lo è per definizione). Tra i due punti chiamati UO vi sono esattamente 93 miliardi di anni luce misurati lungo la retta che li congiunge. Questa retta si discosta poco dall’origine di tutto, ma non potrà mai coincidere con essa per motivi di scarsa illuminazione… (i fotoni erano ancora intrappolati nella densa zuppa primordiale). Tutte le linee di Universo sono ovviamente delle rette parallele che hanno sempre la stessa distanza tra loro (ad esempio, quella di OGGI).

L’unica cosa che cambia veramente è il punto all’infinito, ossia il Big Bang. Non è più un punto, ma è una retta, così come capitava nella Fig. 3. Vi turba molto? Direi di no. Il tempo rimane zero ed è giusto dato che non esiste un “prima”. Lo spazio è infinito e non nullo. Ma non abbiamo sempre detto che l’Universo è sempre stato infinito, fin dal primo momento, dato che non esisteva niente al di fuori di esso? E allora? Che problema c’è a disegnarlo come una retta. E poi, una retta o un punto ci fanno passare da un concetto a un altro, dallo zero a infinito, che sono legati in modo indissolubile (come ormai sappiamo bene dalle prime due lezioni di matematica). Un qualcosa che può essere un punto senza dimensioni ma anche una retta infinita rende bene l’idea della singolarità. Il Big Bang è un punto singolare, rappresentabile come vogliamo, tanto per lui dimensioni e tempo non hanno significato. Fisicamente, potremmo anche ammettere che era zeppo di energia o di pre-particelle o di quello che volete. Per queste strane cose lo “spazio” c’era e anche quanto ne volevano (tra poco lo definiremo ancora meglio).

Nota Bene 1: ho semplificato enormemente la trattazione dell’espansione dello spazio-tempo e delle coordinate comoventi. Per essere precisi bisognerebbe introdurre il tempo e la sua definizione (tempo nostro, tempo cosmologico e fenomeni relativistici collegati). Non sono cose impossibili da spiegare, ma per adesso fermiamoci qui e digeriamo concetti apparentemente ovvi ma difficili da digerire o -meglio ancora- concetti apparentemente complicati, ma di una banalità assoluta. In entrambe le visioni la mente deve, comunque, lavorare…

Nota Bene 2: per semplicità abbiamo lavorato con un punto e una retta. Ma la retta poteva essere considerata un piano (passando a due dimensioni) o addirittura uno “spazio”(passando a tre). Quel punto acquista, allora, un valore ben più realistico e inquietante. Un punto di dimensioni nulle e, contemporaneamente, un vero spazio di dimensioni infinite ma senza tempo. Come volevasi dimostrare!

Divertitevi a riflettere su quest’ultima nota… è molto divertente, anche se la testa inizierà a girare un pochino.

Un'ultima riflessione. Ho seguito una similitudine tra punto all'infinito e Big Bang. Mi è servita per far comprendere il passaggio da una rappresentazione a un'altra. Tuttavia, la similitudine non può essere completa per varie ragioni. La più importante è che mentre il punto delle rette parallele è veramente all'infinito, il Big Bang non lo è. Esso infatti si può raggiungere: basta muoversi di 13.8 miliardi di anni nel passato. Quindi, vi prego, non esasperate la similitudine, che è servita solo per semplificare un passaggio non del tutto banale.

 

Chi avrà creato il Big Bang? Parliamone...