13/02/16

Destinato ai solutori più che abili ****

Questo esercizio non è assolutamente necessario per proseguire nella dinamica relativistica. E’ un “di più” che può essere utile per mettersi alla prova sulla RR e per prepararsi in anticipo alla discussione sull’uguaglianza tra massa ed energia, caposaldo einsteiniano.

In questo “quiz” vogliamo fare qualcosa di molto simile a quanto ottenuto nell’ultimo capitolo sulla dinamica relativistica (QUI). Imponiamo qualcosa e troviamo qualcos’altro. Cambiamo solo il tipo di esperimento. Finora ci siamo limitati agli urti elastici, dove si conserva anche l’energia cinetica. Tuttavia, perché non usare anche gli urti anelastici in cui sappiamo che non si conserva? Vedremo in seguito come la RR legherà in modo strettissimo la conservazione della massa con quella dell’energia cinetica, cambiando drasticamente la visione della fisica.

L’esperimento è molto semplice e usa solo componenti orizzontali delle velocità, come dimostrato in Fig. 1

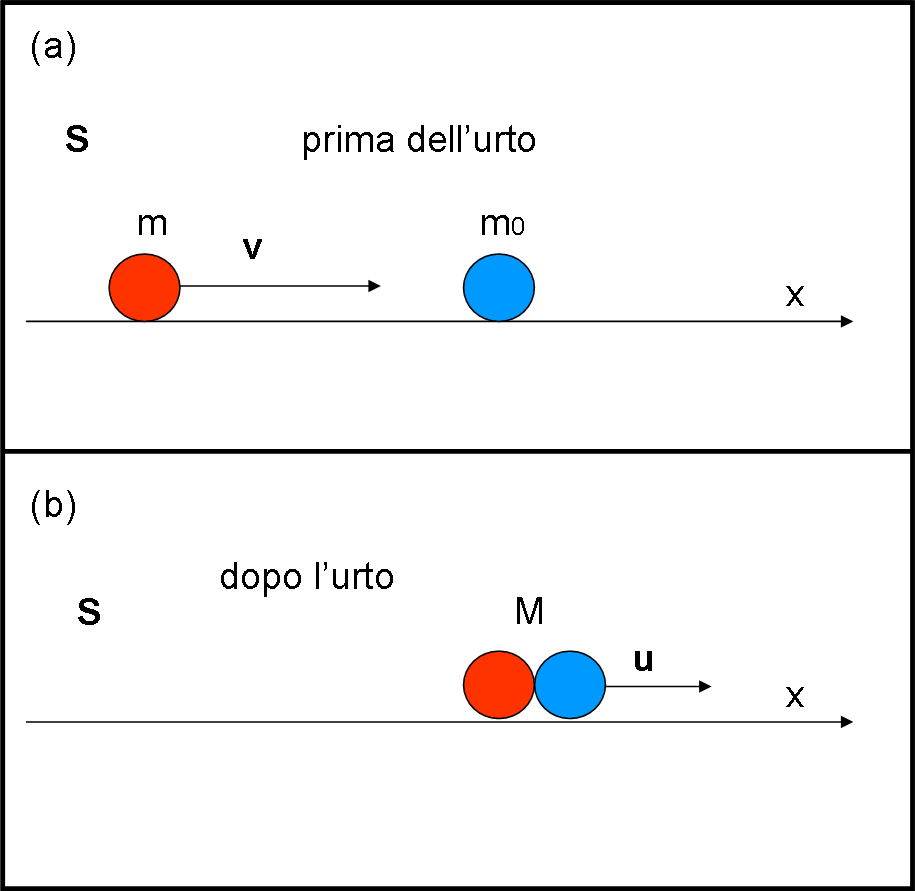
Un corpo di massa a riposo m₀ viaggia a velocità v verso un altro corpo immobile di pari massa a riposo m₀(Fig. 1a). L’urto è completamente anelastico, ossia i due corpi si uniscono e si muovono insieme a velocità u (Fig. 1b).

Il problema parte da due assunzioni:

(1) Imponiamo la conservazione della massa relativistica (non della massa a riposo, mi raccomando!)

(2) Imponiamo la conservazione della quantità di moto.

La (1) e la (2) si traducono in:

M = m + m₀ …. (1)

Attenzione non abbiamo imposto M = 2m₀, dato che una massa corrisponde a una velocità v (su questa problematica ci torneremo molto presto).

mv = Mu = (m + m₀)u …. (2)

Quello che vogliamo determinare è il rapporto tra m₀ e m e “sperare” di ottenere il risultato ormai ben noto, ossia:

m₀/m = (1 – v²/c²)^1/2

Attenzione: la velocità è quella giusta, dato che è quella legata alla massa m in movimento!

Un aiuto iniziale…

La (2) ci dice:

mv = Mu = (m + m₀)u

mv = mu + m₀u

m(v - u) = m₀u

m₀/m = (v - u)/u = v/u - 1

Determinare il rapporto m/m₀ vuole dire determinare il rapporto v/u

Come possiamo riuscirci? Basta vedere lo stesso fenomeno da un sistema di riferimento S’ che si muova con velocità v rispetto a quello S che abbiamo considerato finora e poi imporre di nuovo la conservazione della quantità di moto, tenendo conto della composizione delle velocità…

Abbiamo a che fare solo e soltanto con una equazione di secondo grado, di cui una sola soluzione è accettabile… matematica elementare, ma un po’ di ragionamento e di perfetta comprensione del principio di relatività.

Io ho in mente un certo procedimento, ma non è detto che sia l’unico… come abbiamo già visto molte volte.

Buon divertimento…

Qui potete trovare la soluzione del quiz

http://www.infinitoteatrodelcosmo.it/2016/02/19/soluzione-del-quiz-relativistico-destinato-ai-piu-abili/

16 commenti

Fabrizio

13/02/2016 at 23:11

Ci provo.
Per chiarirmi le idee ricapitolo le assunzioni del quiz.

Dei risultati visti negli articoli precedenti posso utilizzare quello della composizione della velocità, ma non quello sulla massa relativistica perchè è quello che cerchiamo.

Per evitare di confondermi con velocità e masse dei 3 oggetti quando hanno lo stesso valore, come mi è successo più volte, le indico esplicitamente. Uso il pedice r per l'oggetto rosso (R), il pedice b per l'oggetto blu (B) e il pedice i per l'insieme dei due oggetti dopo l'urto. Non aggiungo indicazioni di prima e dopo l'urto perchè sono già contenute in quelle sopra: r e b sono prima e i è dopo.

Nel sistema di riferimento S della figura, quello dove R è fermo, abbiamo:

Velocità   Masse relativistiche
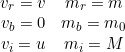$\inline \begin{matrix} v_r=v& m_r=m& \\ v_b=0& m_b=m_0& \\ v_i=u& m_i=M& \end{matrix}$      essendo fermo in questo sistema di riferimento

Non uso l'espressione della massa relativistica che abbiamo visto nel 4° articolo sulla dinamica relativistica, perchè la voglio trovare nuovamente con questo ragionamento. Quindi m e M rimangono incognite.

Applico il principio di conservazione della massa relativistica
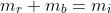$m_r+m_b=m_i$    che con le sostituzioni viste sopra diventa
$m+m_0=M$

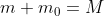
Applico il principio di conservazione della quantità di moto
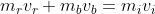$m_r v_r+m_b v_b=m_i v_i$      che con le sostituzioni viste sopra diventa
$m v=M u$

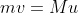
Metto insieme i due risultati e ottengo
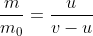$\frac{m}{m_0}=\frac{u}{v-u}$ volendo evidenziare u che considero come una incognita
$u=\frac{m v}{m_0+m}$

Fin qui bene, aveva già fatto tutto Vincenzo.

Ora provo a rifare tutto nel sistema di riferimento S' che si muove con velocità v rispetto a S.

Velocità                       Masse relativistiche

$\begin{matrix} v'_r=0& m'_r=m_0&\textup{qui\,e'\,fermo\,R}\\ v'_b=-v&m'_b=m&(*)\\ v'_i=(u-v)/(1-u v/c^2)\, (**) & m'_i=M'& \end{matrix}$

(*) ho assunto che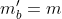 $m'_b=m$ poichè B in S' ha una velocità uguale in valore a quella di R in S, non sono sicuro che questo basti

(**) applico la legge di composizione delle velocità

Applico il principio di conservazione della massa relativistica
$m'_r+m'_b=m'_i$    che applicando le sostituzioni viste sopra diventa
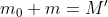$m_0+m=M'$          quindi M=M'

Applico il principio di conservazione della quantità di moto
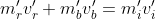$m'_r v'_r+m'_b v'_b=m'_i v'_i$    che applicando le sostituzioni viste sopra diventa
$-v m=M' (u-v)/(1-u v/c^2)$         sostituendo M'
$-v m=(m_0+m) \frac{(u-v)}{(1-\frac{u v}{c^2})}$

Ricapitolando, le due equazioni ottenute sono:

$u=\frac{m v}{m_0+m}$

$-v m=(m_0+m) \frac{(u-v)}{(1-\frac{u v}{c^2})}$

Poichè voglio trovare la relazione tra m e v, devo eliminare u.

Elaboro la seconda equazione per estrarre u.

$-m v \left( 1-\frac{u v}{{{c}^{2}}}\right) =\left( \mathit{m_0}+m\right) \left( u-v\right)$    che espando in

$\frac{m u {{v}^{2}}}{{{c}^{2}}}-m v=-m_0 v-m v+m_0 u+m u$ elimino i termini comuni a dx e sx e per facilitare la manipolazione sostituisco $\frac{{{v}^{2}}}{{{c}^{2}}}$ con ${A}^{2}$

$m u {{A}^{2}}-m_0 u-m u=-m_0 v$    ora posso isolare u

$u=-\frac{{m_0} v}{m {{A}^{2}}-{m_0}-m}$        per eliminare u la sottraggo a $u=\frac{m v}{m_0+m}$

$0=\frac{{m_0} v}{m {{A}^{2}}-{m_0}-m}+\frac{m v}{{m_0}+m}$ elimino la v ( $v\neq 0$ ) ed espando

$0=\frac{{{m}^{2}} {{A}^{2}}+{{{m_0}}^{2}}-{{m}^{2}}}{\left( m{m_0}+{{m}^{2}}\right) {{A}^{2}}-{{{m_0}}^{2}}-2 m {m_0}-{{m}^{2}}}$ per essere 0 deve essere 0 il numeratore

${{m}^{2}} {{A}^{2}}+{{{m_0}}^{2}}-{{m}^{2}}=0$

$\left( 1-{{A}^{2}}\right) {{m}^{2}}={{{m_0}}^{2}}$      che ha due soluzioni

$m=\pm \frac{{m_0}}{\sqrt{1-A^{2}}}$ assumendo che la massa rimanga positiva e ricordando cosa è A

$\mathbf{m=\frac{{m_0}}{\sqrt{1-\frac{{{v}^{2}}}{{{c}^{2}}}}}}$    che è quella che cercavamo.
Vincenzo Zappalà

14/02/2016 at 07:33

caro Fabrizio...

penso che tu l'abbia complicata fin troppo...

Il fatto di avere trovato la relazione tra la tua incognita (m0/m) e il rapporto delle velocità prima e dopo l'urto (v/u) ti permette di non considerare più le masse e lavorare solo con le velocità. Dalla conservazione della qm visto da S' ottieni subito la relazione tra la u e la u' che è però anche data dalla composizione delle velocità. Ed ecco arrivare l'equazione che non contiene alcuna massa, ma solo il rapporto v/u che è poi quello che ti basta...

Provaci (anche se non dico che tu abbia sbagliato...)...
Fabrizio

14/02/2016 at 09:54

Mi sembrava di avere lavorato troppo di "forza" rispetto al tuo suggerimento di considerare il rapporto tra velocità.

Ci provo ancora.

Intanto ti ringrazio per questa tua attività di grande divulgazione.

Avevo già tentato di studiare da autodidatta la RR ed altri temi di fisica, ma ogni tuo articolo mi fa capire che non avevo capito qualcosa.
Umberto

14/02/2016 at 10:13

$v\cdot m=(m_{0}+m)\cdot u$

$-v \cdot m=(m_{0}+m) (u-v)/(1-uv/c^{2})$

dividendo membro a membro:

$(u-v)/(1-uv/c^{2})=-u$ 1)

pongo v/u=x; u=v/x

sostituisco nella 1

$(v/x-v)/(1-v\cdot v/x c^{2})=-v/x$

e dividendo per v membro a membro:

$(1/x-1)/(1-v^{2}/c^{2}x)=-1/x$

abbiamo ora una equazione in x

dopo svariati passaggi si arriva all'equazione:

$X^{2}-2\cdot X -v^{2}/c^{2}=0$

$X_{1,2}=1 \pm \sqrt{1+ v^{2}/c^{2}}$

prendo il segno + altrimenti sarebbe negativo

quindi

$v/u=1 + \sqrt{1+ v^{2}/c^{2}}$

$v/u-1= \sqrt{1+ v^{2}/c^{2}}=m_{0}/m$
Vincenzo Zappalà

14/02/2016 at 10:24

occhio Umberto che nella massa relativistica, sotto la radice quadrata, deve esserci

1 -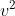 $v^{2}$ / $c^{2}$ .....

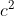un consiglio anche per te... prova a lavorare solo con le velocità...
Vincenzo Zappalà

14/02/2016 at 10:32

caro Fabrizio,

ti ringrazio... e spero di chiarirti sempre più le idee adesso che stiamo per entrare nella parte più... "calda" ed ... energetica!
Umberto

14/02/2016 at 17:45

scusa , c'è un errore di segno nell'equazione di secondo grado (e non è colpa di latex):

$X^{2}-2\cdot X +v^{2}/c^{2}=0$

che riporta a:

$X_{1,2}=1 \pm \sqrt{1- v^{2}/c^{2}}$

$v/u=1 + \sqrt{1- v^{2}/c^{2}} v/u-1= \sqrt{1- v^{2}/c^{2}}=m_{0}/m$

per il resto fin dal secondo passaggio ho eliminato la massa e lavorato

solo con le velocità
Vincenzo Zappalà

14/02/2016 at 18:08

ottimo Umberto... ma non dico ancora niente perché so che Paolino è impegnato...

Bravi ragazzi, sono fiero di voi... comunque vada....

e se poi ci provasse qualcun altro ?????
Fabrizio

14/02/2016 at 18:28

Forse ci sono.

Notando che in S' lo scenario è esattamente speculare rispetto a quello in S, la velocità dopo l'urto dell'insieme dei due corpi deve essere uguale e contraria a quella in S. Francamente ci sono arrivato con i calcoli, ma avrei dovuto accorgermene anche a vista in base alla simmetria delle due situazioni.

Quindi la velocità dopo l'urto è $v'_i=-v_i=-u$ .

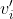Ma $v'_i$ deve anche rispettare la legge di composizione delle velocità, quindi:

$\mathit{v'_i}=\frac{u-v}{1-\frac{v u}{{{c}^{2}}}}=-u$

dalla quale portando tutto a destra si ottiene

$\frac{v {{u}^{2}}}{{{c}^{2}}}-2 u+v=0$

che è una equazione di 2° grado che ha queste soluzioni

$u=\frac{1\pm \sqrt{1-\frac{{v}^{2}}{{c}^{2}}}}{\frac{v}{{c}^{2}}}$

inserendolo in $\frac{\mathit{m_0}}{m}+1=\frac{v}{u}$ diventa

$\frac{\mathit{m_0}}{m}=\frac{\frac{{{v}^{2}}}{{{c}^{2}}}}{1\pm \sqrt{1-\frac{{{v}^{2}}}{{{c}^{2}}}}}-1$

che facendo il MCD e ricordando che ${1-\frac{{{v}^{2}}}{{{c}^{2}}}}=\left (\sqrt{1-\frac{{{v}^{2}}}{{{c}^{2}}}} \right )^{2}$

$m=\mp \frac{m_0}{\sqrt{1-\frac{{{v}^{2}}}{{{c}^{2}}}}}$

scartando la soluzione negativa perchè non fisica (a meno che non ci sia lo zampino dell'antimateria?)

$\mathbf{m=\frac{m_0}{\sqrt{1-\frac{{{v}^{2}}}{{{c}^{2}}}}}}$
Vincenzo Zappalà

14/02/2016 at 18:29
Daniela

14/02/2016 at 22:43

Domanda banale: suggerisci di osservare il fenomeno da S' che si muove a velocità v rispetto a S... Quindi la stessa velocità v a cui si muove la pallina rossa prima dell'urto?
Paolo

15/02/2016 at 03:50

Caro Enzo grazie per avermi aspettato...

Ho sbirciato le altre soluzioni e mi accorgo di aver usato un approccio leggermente diverso... e non sono così sicuro che sia corretto.

Dunque visto da S, prima dell'urto:

la pallina Blu è ferma la sua velocità è zero, q(b) = m(0) v = 0

la pallina Rossa invece si muove a velocità v, q(r) = m v

Dopo l'urto:

Entrambe le palline hanno una nuova massa M e si muovo con una nuova velocità u

q(d) = M u

dato che prima dell'urto solo la pallina rossa si muove deve valere che:

m v =M u

v/u = M/m questo rapporto tra masse e tra velocità lo chiamo K

da cui segue che u = v/K

v/u = (m(0) +m)/m = m(0)/m +1

m(0)/m = v/u - 1 = (k – 1)

Visto da S', prima dell'urto:

la pallina Blu si muove con velocità -v.......... q'(b) = m''(-v)

la pallina Rossa invece si muove alla stessa velocità del sistema S', per cui per lui è ferma: q'(r) = m'(0) 0 = 0

Dopo l'urto:

Entrambe le palline hanno una nuova massa M' e si muovo con una nuova velocità u'

q'(d) = M'u'

dato che prima dell'urto solo la pallina blu si muove deve valere che:

- m''v = M' u'

-v/u' = M'/m'' questo rapporto tra masse e tra velocità lo chiamo K'

da cui segue che u' = -v/K'

-v/u' = (m' +m'(0))/m' = m'(0)/m' +1

m'(0)/m' = -v/u' - 1 = (-k' – 1)

La velocità u', deve tener conto sia della velocità negativa della pallina blu, sia della composizione relativistica delle velocità.

Voglio trovare la relazione tra K e K':

u' = (u-v)/(1- vu/c²)

v/K'= (v/K -v)/(1- v²/Kc²) = (v-vk)/K /(Kc²- v²)/Kc²

v/K'= c² (v-vk)/(Kc²- v²)

v/K'= c²v (1-k)/(Kc²- v²)

1/K'= c² (1-k)/(Kc²- v²)

(Kc²- v²)/c²= K' (1-k)

K- v²/c²= K' (1-k)............... aggiungo 1

1 + K - v²/c² = K' (1-k). +1

1 - v²/c² = K' (-K +1) +1 – K

1 - v²/c² = K' (-K +1) (-K+1)

1 - v²/c² = (-K+1) (K' +1) cambio segno

1 - v²/c² = (K -1) (-K' -1)

ma k-1 = m(0)/m …......................cambio m con la sua massa relativistica

k-1 = m(0)/m(0)/√(1- v²/c²)

k-1 = √(1- v²/c²)

1- v²/c² = √(1- v²/c²) (-K' -1)

(1- v²/c²)/√(1- v²/c²) = (-K' -1)

√(1- v²/c²) = (-K' -1)

ma (-k – 1) = m'(0)/m'

√(1- v²/c²) = m'(0)/m'

m' = m'(0)/√(1- v²/c²)

Inoltre

1- v²/c² = (-K' -1) (k -1)

1- v²/c² = (m'(0)/m') (k -1) √(1- v²/c²) = m'(0)/m'

1- v²/c² = √(1- v²/c²) (k -1)

√(1- v²/c²) = (k -1)

ma (k -1) = m(0)/m

√(1- v²/c²) = m(0)/m

m = m(0)/√(1- v²/c²)

mah.....

Paolo
Vincenzo Zappalà

15/02/2016 at 05:49

mi sa, Paolino, che l'hai complicato un po'.... anche se alla fine tutto sembra tornare...

Una volta che hai scritto la

u' = (u-v)/(1- vu/c²)

basta dire che u' = -u ... per la conservazione della qm e l'equazione è pronta...

Risolta in u/v hai subito m/m0 ...

Comunque, sempre bravi i miei assistenti, anzi... sempre più bravi!!!
Vincenzo Zappalà

15/02/2016 at 05:50

certo Daniela,

in modo che quella che prima si muoveva adesso è ferma...
Daniela

15/02/2016 at 06:59

Perfetto! Questa condizione dovrebbe semplificare i calcoli e volevo esserne sicura prima di applicarla...
Paolo

15/02/2016 at 10:48

Mi sono reso conto che in realtà potevo farla più breve e tra l'altro senza imporre la massa relativistica, ma ricavandola.

Una volta arrivato qui:

1 - v²/c² = (K -1) (-K' -1)

(1 - v²/c²) = (m(0)/m) (m’(0)/m’)

Basta ricordare che m(0) = m’(0) (le due palline sono ferme nei rispettivi sistemi di riferimento, per cui le masse sono legate a v=0), e che m = m’, dato che la velocità è la stessa (le due masse viaggiano sia in S che in S’ alla stessa velocità, ma in senso inverso) cambia solo il segno della velocità ed ovviamente sono invertite le palline rosse e blu, ne segue che:

(1 - v²/c²) = m(0)²/m²

m(0)/m = +/- √ (1 - v²/c²)

Paolo

Lascia un commento Cancel Reply

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.

Destinato ai solutori più che abili ****

Articoli correlati

Perché si cerca il gravitone? ***

Una favola senza fine: il principe fotone e la bella addormentata Terra ***

I buchi neri non rubano... diamogli solo il tempo! ***

Deflessione della luce per... tutti **

16 commenti

Lascia un commento Cancel Reply