Avevamo lasciato i Papallini intenti a dipingere la circonferenza per mostrare i radianti...

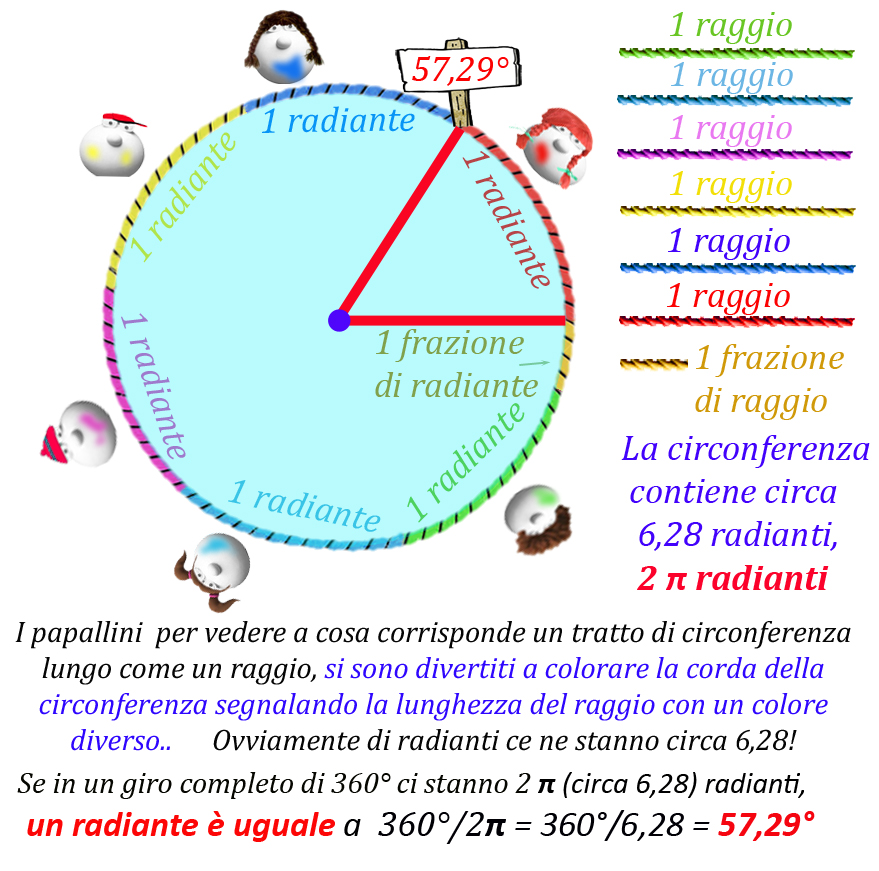
Un giro completo di giostra può essere indicato sia come una rotazione di 360°, sia come una rotazione di 2π radianti (circa 6,28 radianti)...ed è un attimo per Papalmatematico trasformare i gradi in radianti...

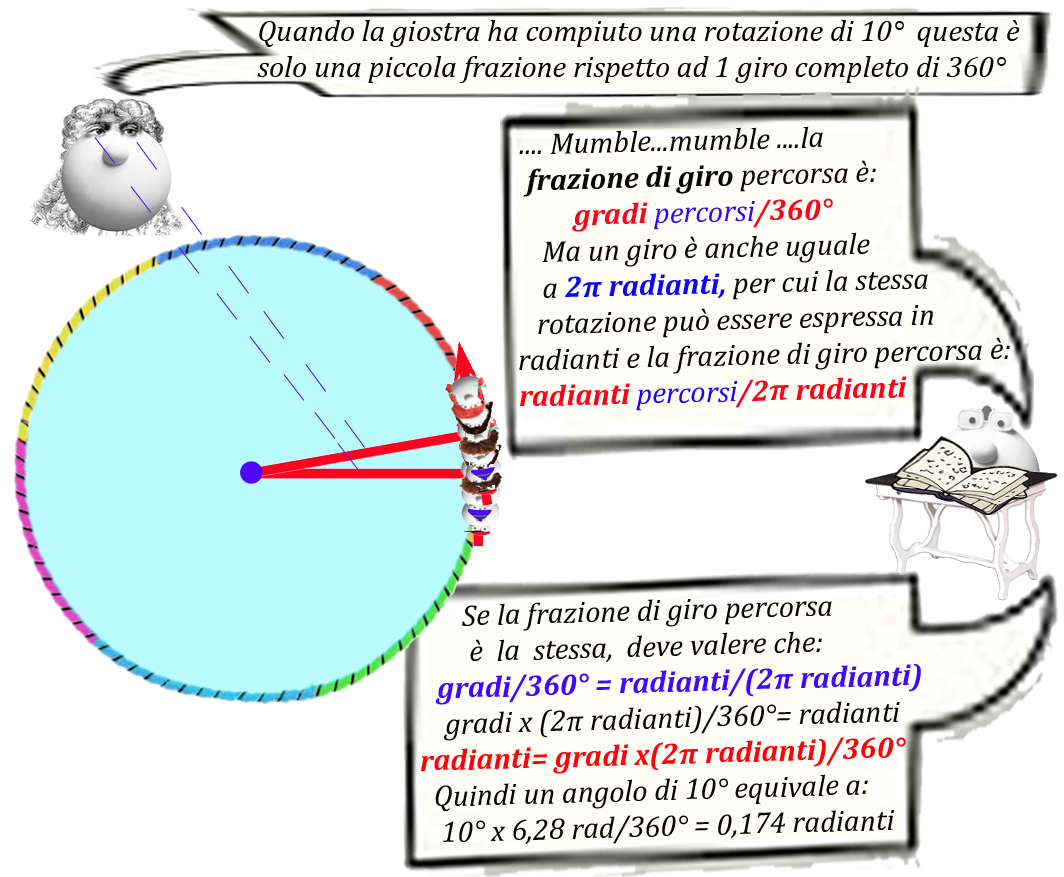
Ovviamente la giostra in un Periodo di tempo pari a 12 secondi ruota di 360° che corrispondono a 2π radianti, ossia circa 6,28 radianti ... per cui la velocità angolare ω può essere espressa, invece che in gradi, in radianti percorsi in un certo Periodo di tempo:

Velocità angolare (ω)= 2π /Periodo

Velocità angolare giostra: 6,28 radianti/12 sec= 0,523 rad/sec

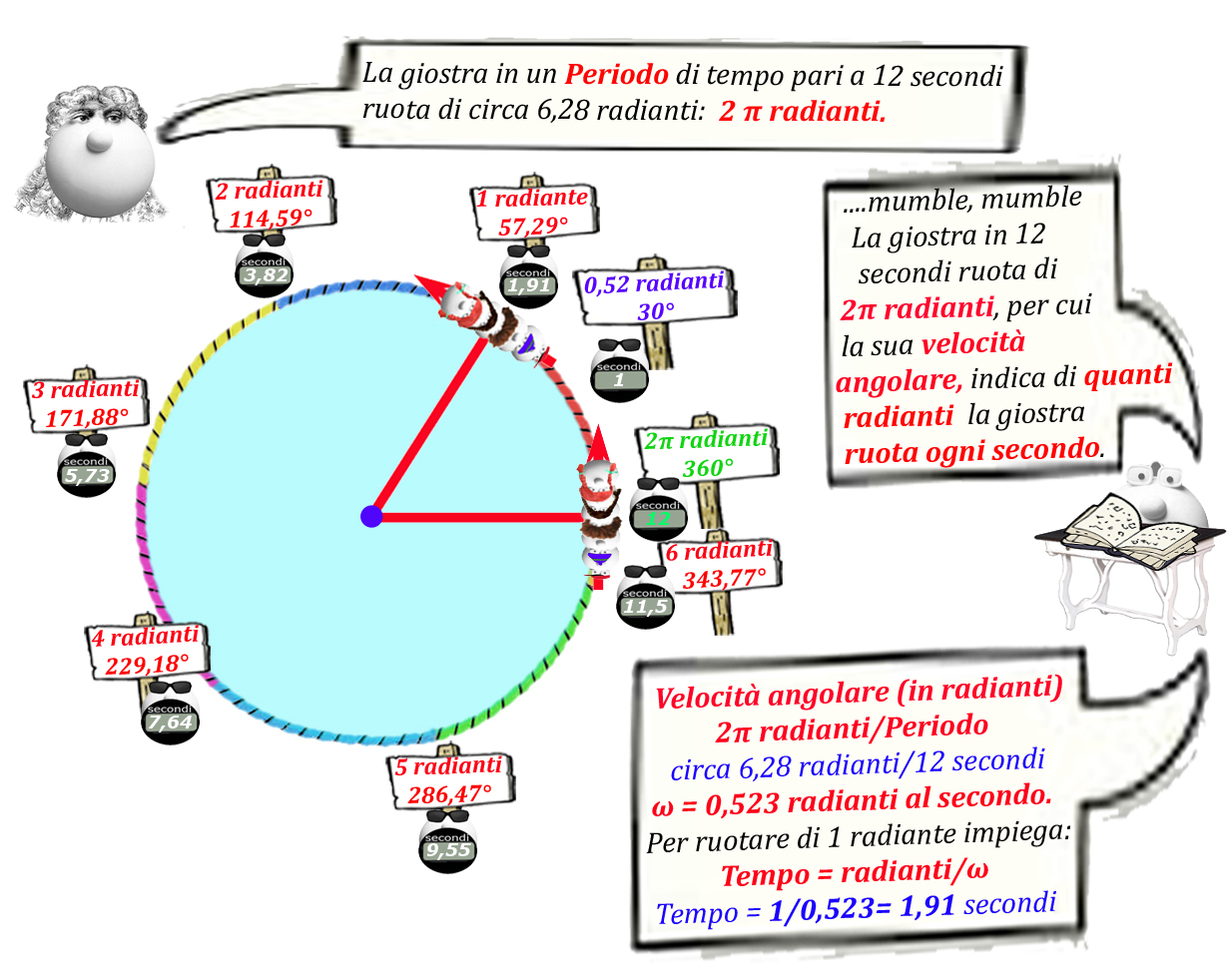
Ogni secondo la giostra compie una rotazione di 0,523 radianti (che corrispondono a 30°), quindi in 2 secondi ruota di:

“Spazio”(in radianti) = Velocità angolare (ω) x tempo

“Spazio” (rotazione giostra) = 0,523 rad/sec  2 sec= 1,046 radianti

Per ruotare di 1 radiante la giostra impiega:

Tempo = “Spazio”(in radianti)/ (ω) Velocità angolare

Tempo = 1 rad/0,523 = 1,91 secondi

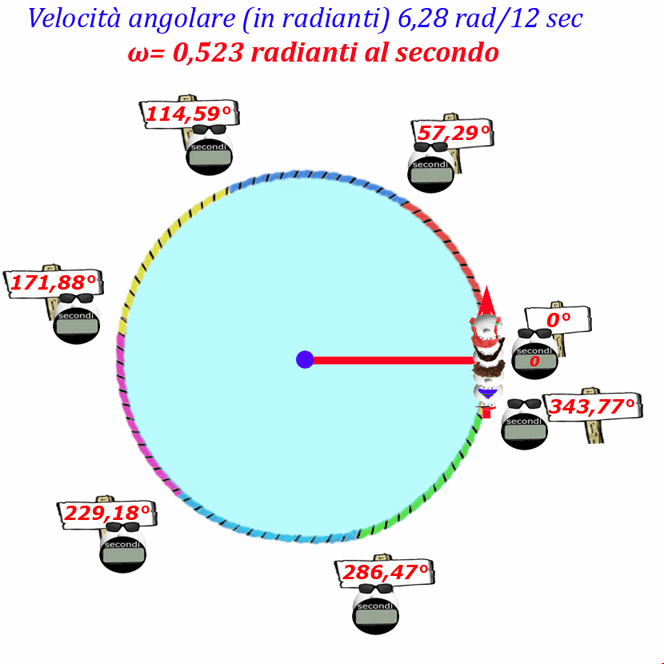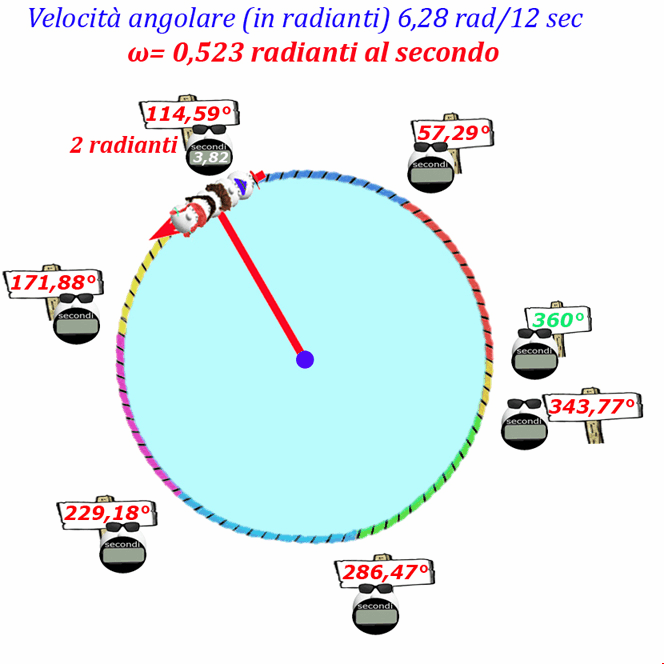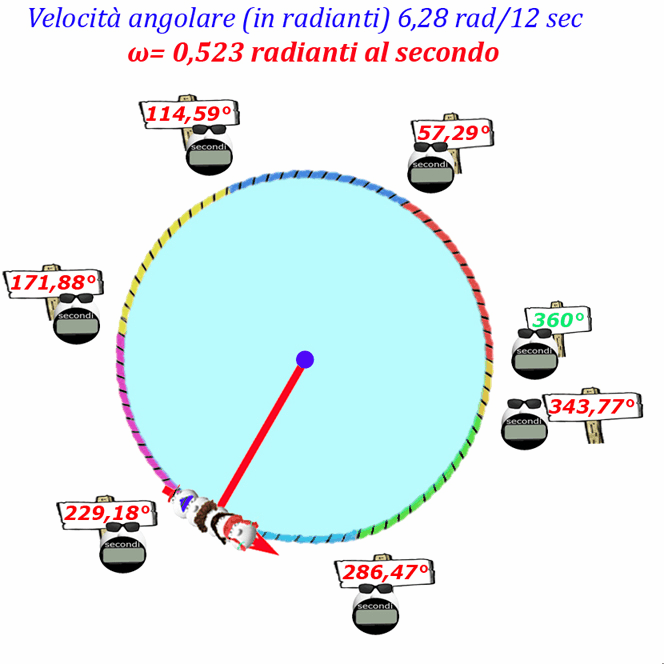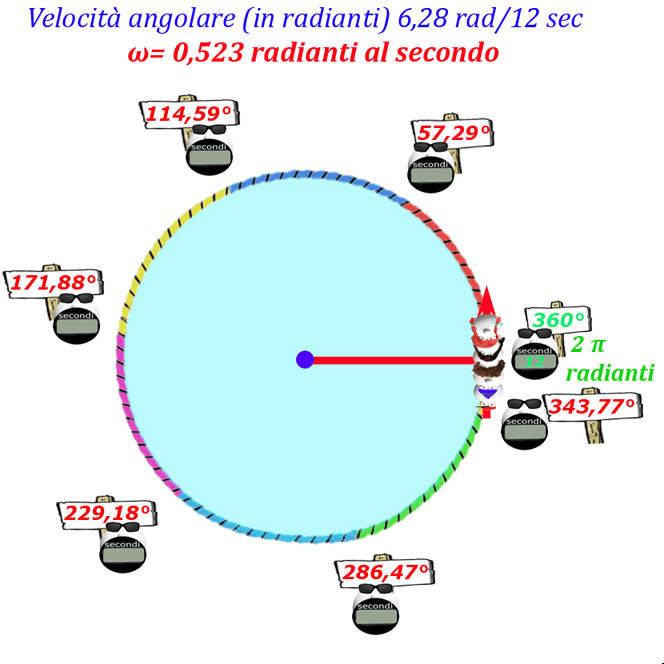
La velocità di rotazione, però, indica quanto rapidamente gira la giostra, ma non con quale velocità i papallini percorrono la circonferenza.

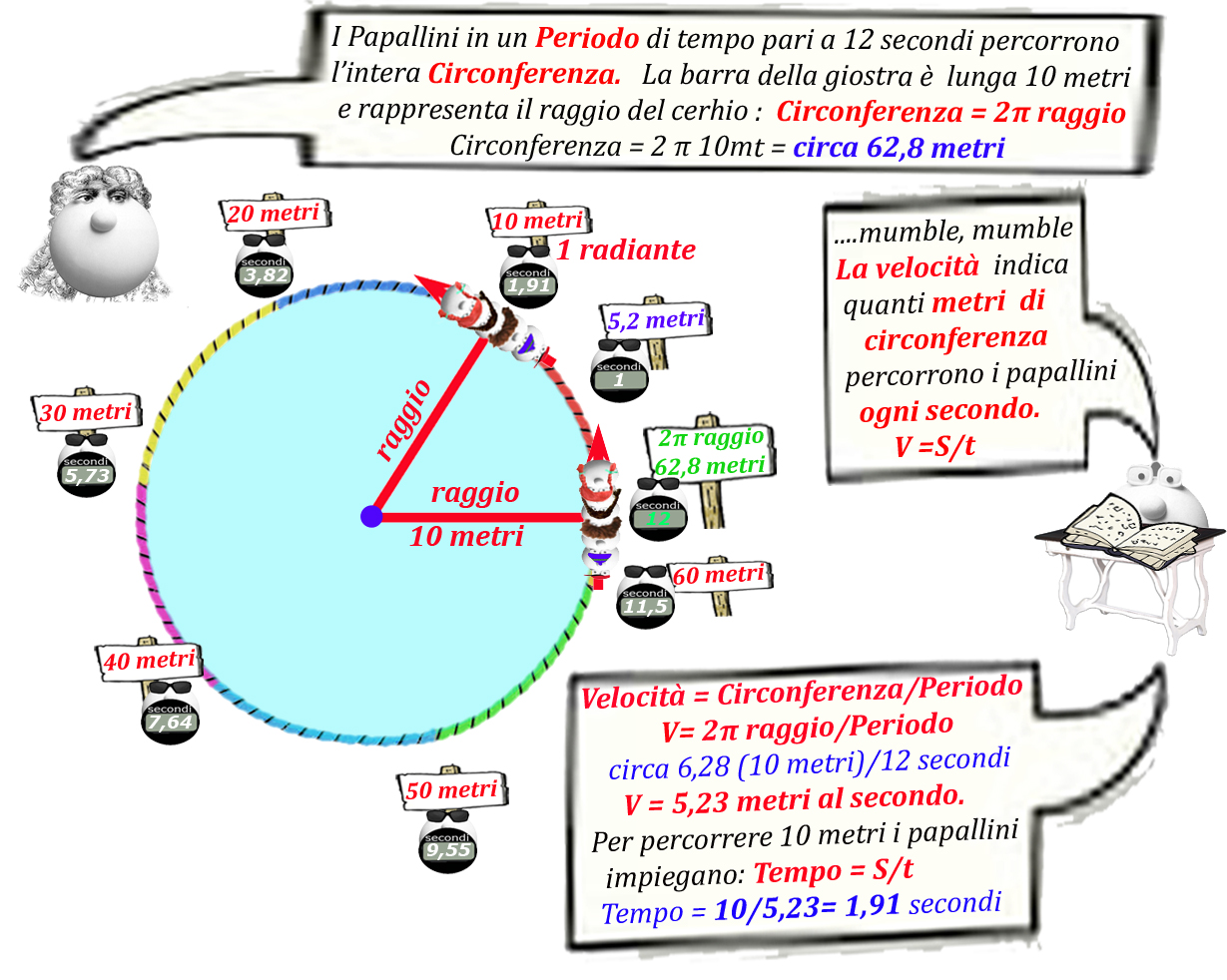
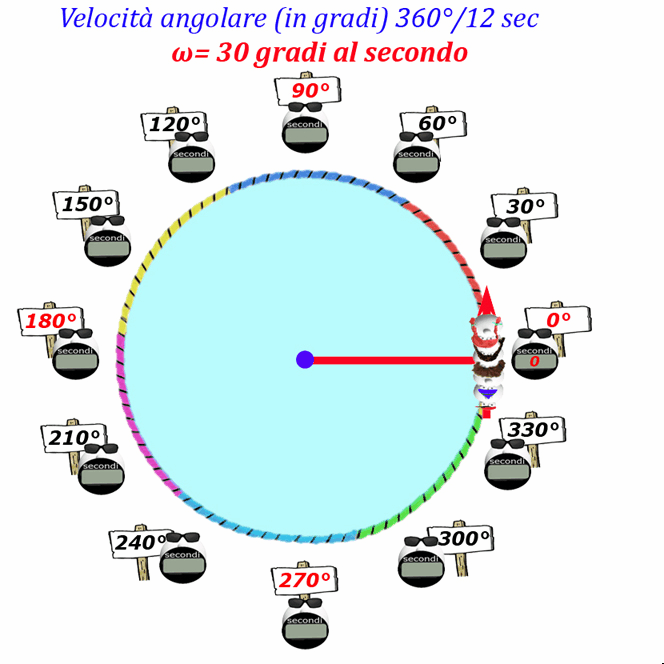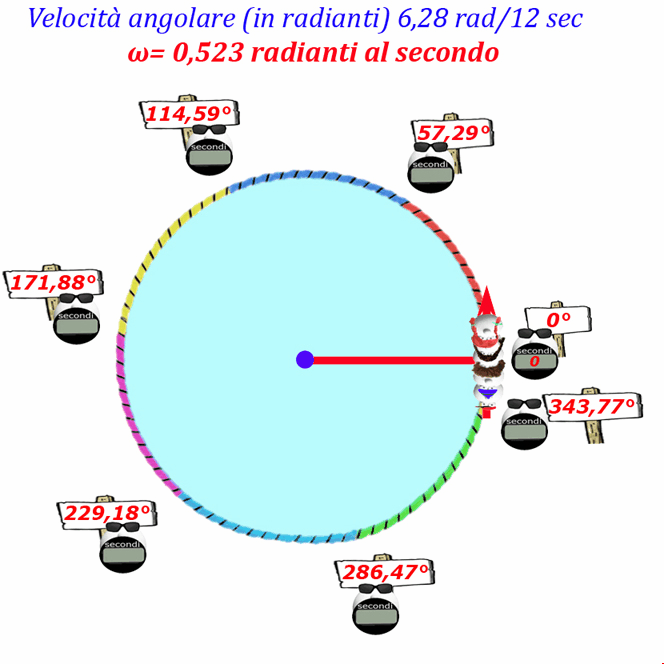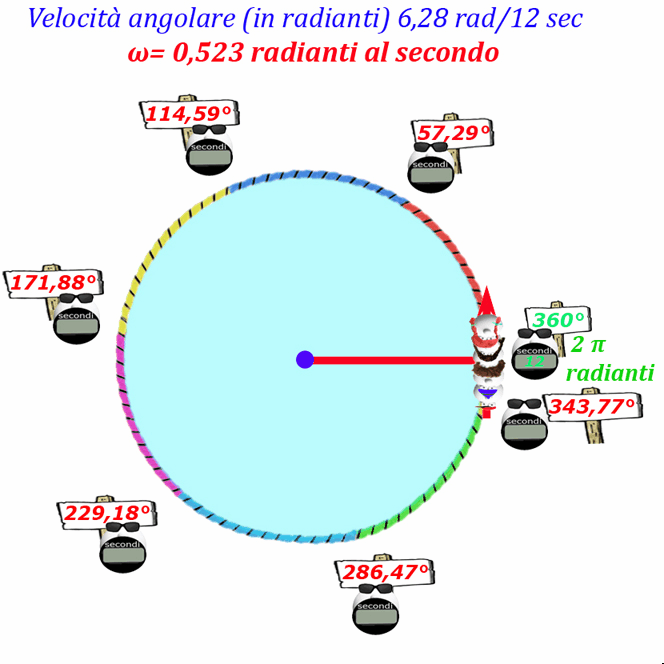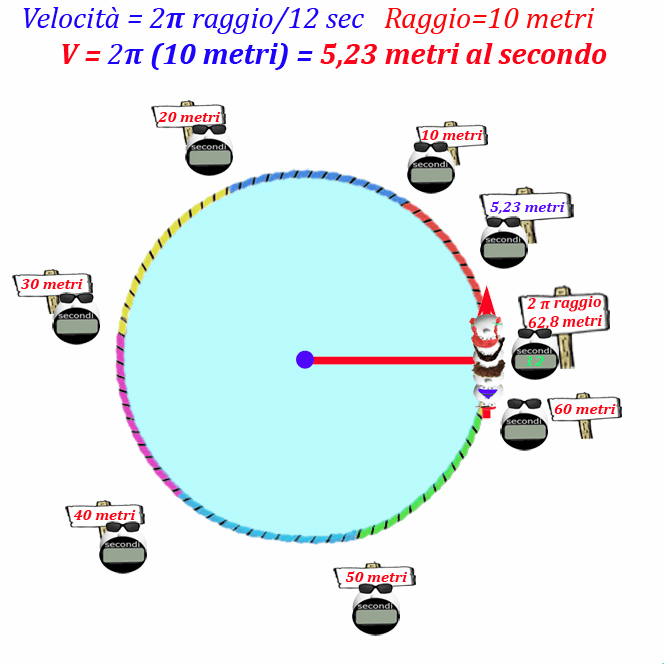
Il modulo della velocità con cui i papallini percorrono la circonferenza (v=S/t) è costante, quindi basta dividere lo spazio percorso, ossia la lunghezza della circonferenza, per il Periodo di tempo impiegato per percorrerla:

Velocità = Circonferenza/Periodo

ma la Circonferenza è uguale al doppio del raggio per pi greco:

Velocità = 2π raggio/Periodo

Se il raggio è di 10 metri

Velocità (papallini) = 2π 10mt/12 sec= circa 5,23 metri/secondo

Ogni secondo i papallini percorrono 5,23 metri, quindi in 10 secondi percorrono un tratto di circonferenza pari a:

Spazio = Velocità x tempo

Spazio (tratto di Circonferenza) = 5,23mt/sec  10 sec=  52,3 metri

… e per percorrere 10 metri i papallini impiegano:

Tempo = Spazio/Velocità

Tempo = 10/5,23 = 1,91 secondi

Nel Papalpark, però, ci sono giostre di dimensioni diverse, per cui più è grande il cerchio, più è grande il raggio e più è lunga la circonferenza da percorrere.

Se si confrontano due giostre di dimensioni diverse che impiegano lo stesso tempo per compiere 1 giro, queste hanno sicuramente la stessa velocità angolare, ma i papallini della giostra più piccola, nel medesimo tempo, percorrono una circonferenza minore di quella dei papallini della giostra più grande, per cui la velocità con cui ognuno dei due gruppi percorre la propria circonferenza non può che essere diversa.

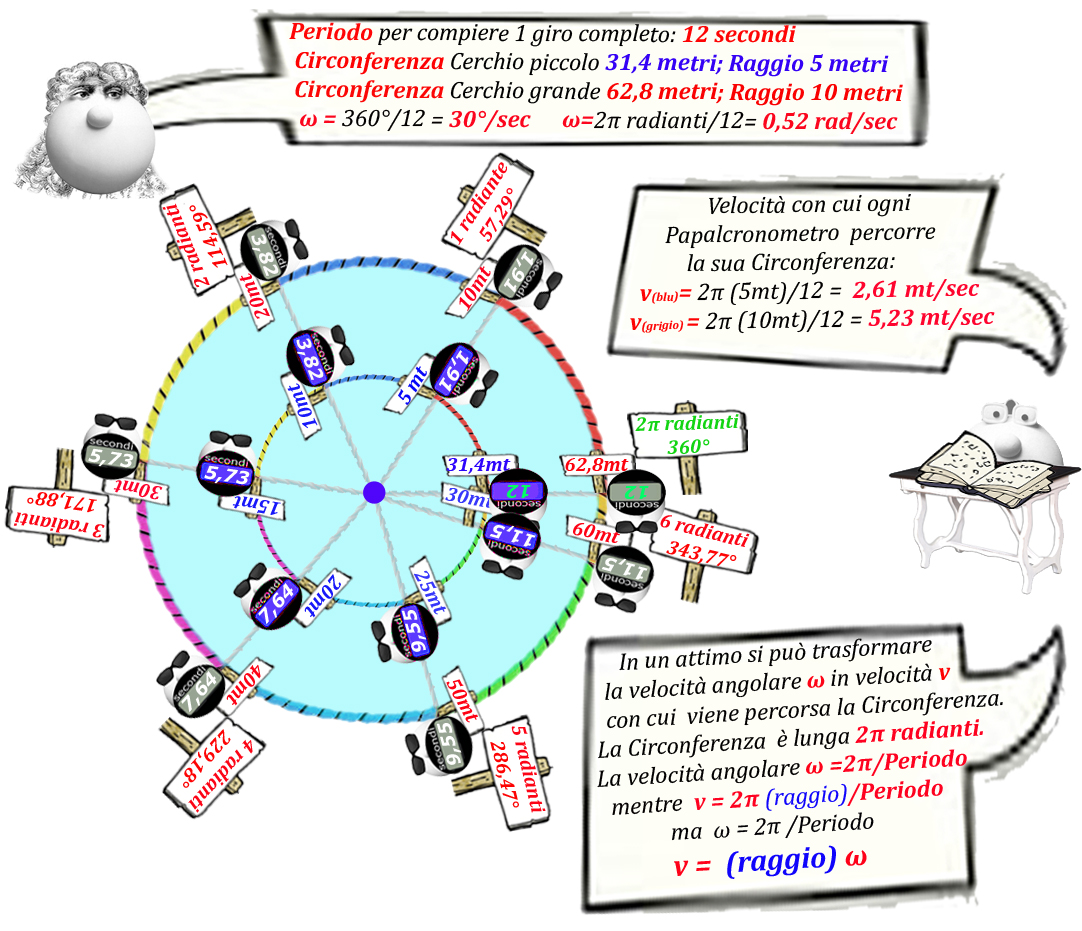
La velocità angolare espressa in radianti che sembrava superflua, al contrario si è rilevata utile, poichè consente di trasformare in un attimo una velocità angolare ω in una velocità V di percorrenza della circonferenza, passando dal periodico moto rotatorio della giostra a quello circolare ed uniforme dei papallini..... basta moltiplicare la velocità angolare per il raggio...

V= ω raggio  ed ovviamente:   ω =V/raggio

PapalNewton stava quasi per incamminarsi verso casa, quando un papallino gli chiede: cosa significa andare via dritti per la tangente?

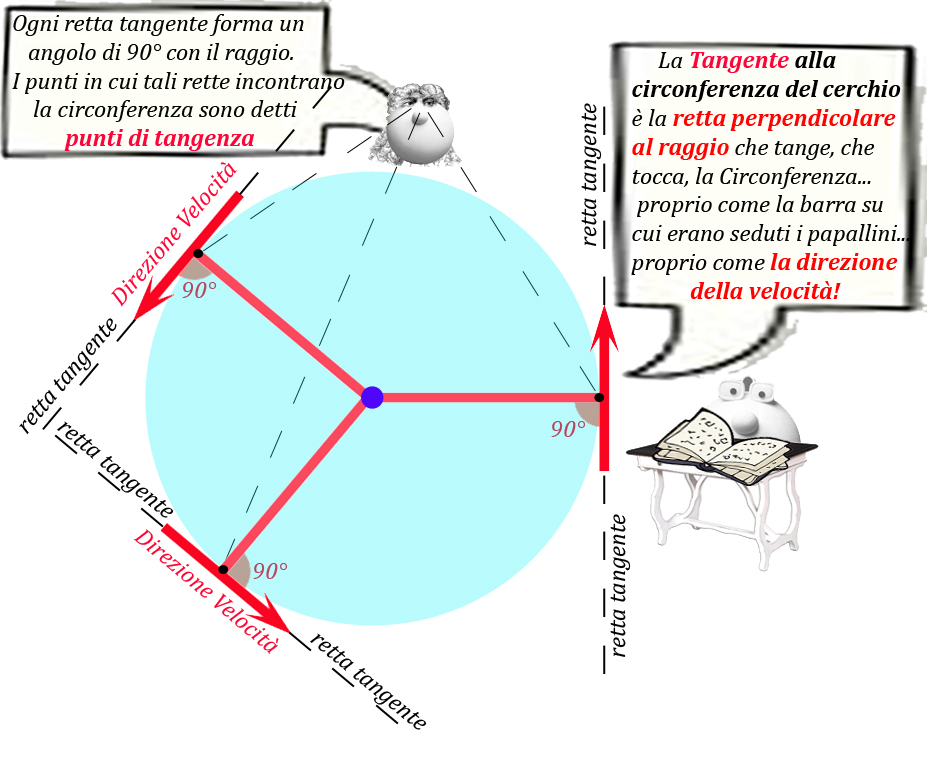
Beh non è poi così difficile da capire.... basta ricordarsi cosa succede alla direzione della velocità dei papallini.... il modulo della velocità non cambia, ma la sua direzione varia continuamente.

La Tangente ad una circonferenza è proprio quella retta perpendicolare al raggio  che tange, che tocca la sua circonferenza  ... proprio come la grande freccia della giostra su cui sono seduti i papallini....

Il punto in cui la retta perpendicolare al raggio (che forma con esso un angolo di 90°) incontra la circonferenza, Papalscherzone lo ha già soprannominato punto di tangenza...

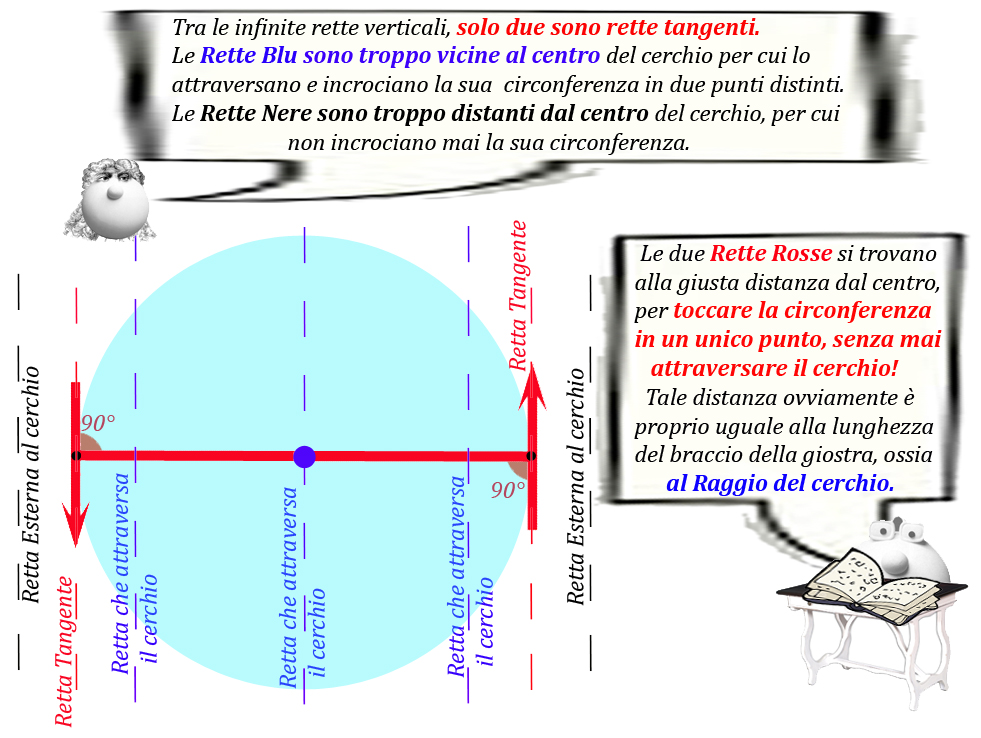
Bella scoperta, afferma PapalNewton, la retta tangente la circonferenza può solo essere perpendicolare al Raggio.... non ha alternative....

E la situazione non può certo esser diversa ruotando la giostra....

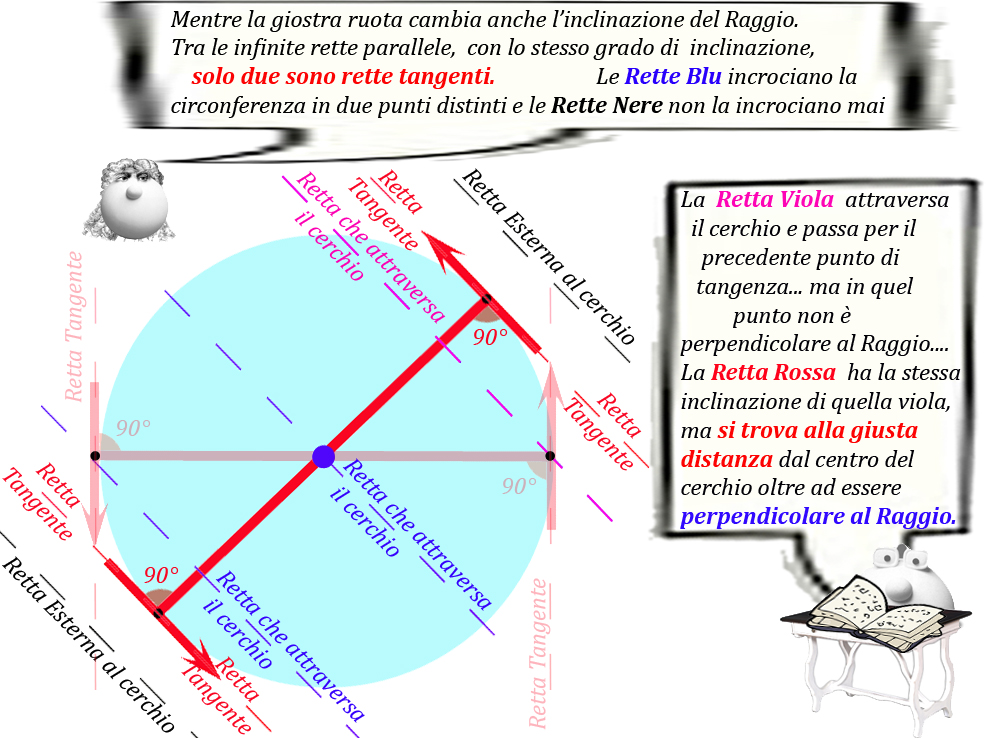
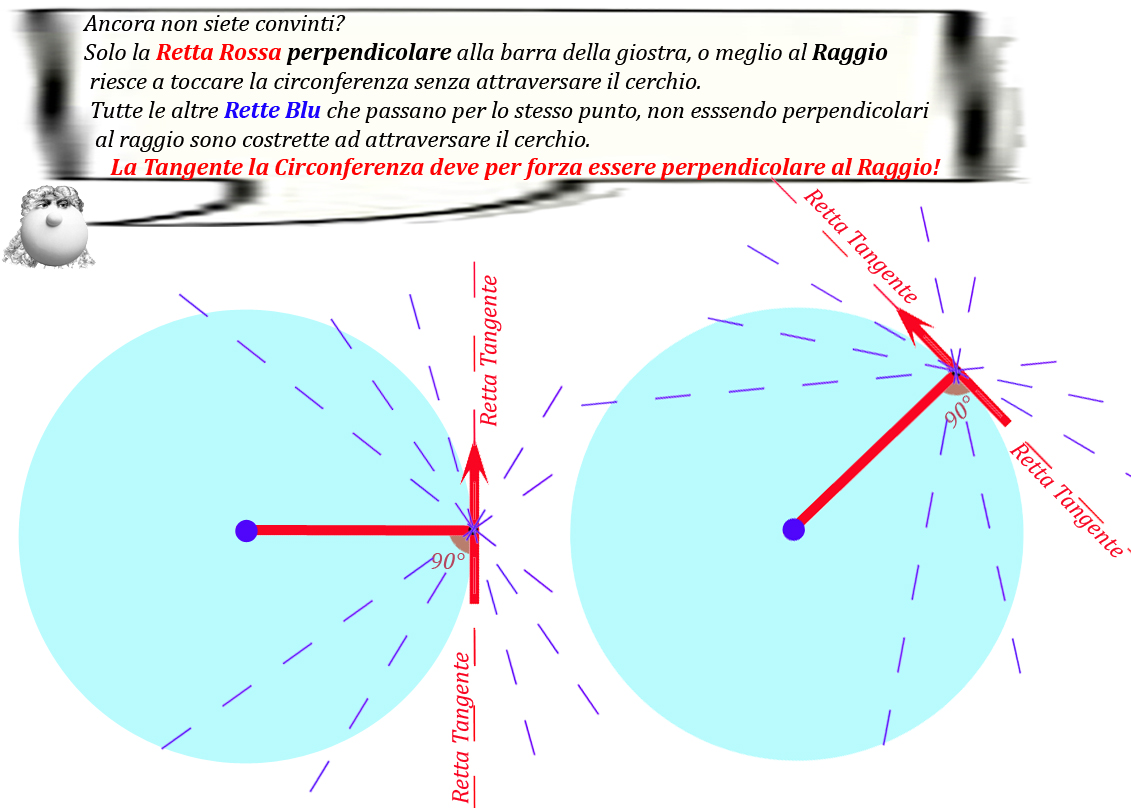
Se la grande freccia non fosse più ancorata al centro della giostra, i papallini e la barra su cui sono seduti proseguirebbero dritti seguendo la direzione della velocità, ossia seguendo la direzione tracciata dalla retta tangente la circonferenza del cerchio.... e quindi andrebbero via per la tangente.. come nel racconto sulla centrifuga  qui .

Papalscherzone ha già soprannominato questa velocità come velocità tangenziale....

Per oggi è tutto dal Pianeta Papalla