Categorie: Relatività
Tags: E=mc2 energia energia a riposo energia cinetica massa relatività ristretta
Scritto da: Vincenzo Zappalà
Commenti:16
Dinamica relativistica. 3: Massa ed energia. 1 ***
Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo
Un po’ ovunque si può trovare la definizione di energia cinetica come lavoro fatto da una forza per portare un corpo da una certa posizione iniziale, in cui è fermo (velocità zero), a una finale con velocità v. Il tutto viene effettuato a partire dal tempo zero per arrivare al tempo t. In poche parole, tempo zero, posizione zero e velocità zero individuano l’inizio del lavoro, mentre s, t e v indicano la fine. Vediamo, ancora, che riusciamo a definire un certo tipo di energia, ma come essa rimanga una grandezza indistinta, ben lontana dal rappresentare qualcosa di "concreto".
Consideriamo il caso più semplice, in cui lo spostamento del corpo avvenga sempre lungo la stessa direzione. Non dimentichiamo mai che il lavoro è una differenza di energie e viene definito come il prodotto scalare (QUI) tra la forza e lo spostamento (due vettori). Dato che stiamo lavorando in una sola direzione, possiamo tranquillamente passare ai moduli e scrivere:
L = F ∆s
Sappiamo già il risultato, ricordando che l'energia cinetica di un corpo fermo è uguale a zero, …
L = F ∆s = KF – KI = ½ mv2(t) – ½ mv2(0) = ½ mv2(t) = K
Partiamo dalla definizione di lavoro e arriviamo alla classica definizione dell’energia cinetica acquisita dopo un certo tempo t, dopo aver percorso lo spazio s e aver raggiunto la velocità v.
Non vogliamo ripetere il calcolo che si può trovare ovunque e che si riferisce alle basi della meccanica classica (basta ricordare il moto uniformemente accelerato). Noi vogliamo utilizzare il calcolo integrale (vedi le lezioni relative agli integrali nell'approfondimento sulla Matematica, dal numero 51 al 61) . D’altra parte dobbiamo proprio sommare tanti prodotti infinitesimi F ds da s = 0 a s = s.
Scriviamo, quindi, senza esitazione (ricordando che v = ds/dt):
L = ∫0s F ds = ∫0s (dq/dt) ds = ∫0s (d(mv)/dt)ds = ∫0t (d(mv)/dt)vdt = ∫0v (v d(mv)
Notate che abbiamo cambiato i limiti di integrazione a seconda della variabile considerata, sapendo bene che a t = 0 corrispondono s = 0 e v = 0 e a t = t corrispondono s = s e v = v (queste erano le ipotesi di partenza e di arrivo)
Nel caso classico, m = m0 = cost.
L = ∫0t F ds = ∫0v m0v dv = ½ m0v2 – ½ m0 0 = ½ m0v2 = K
L’energia cinetica K è proprio data da:
K = ½ m0v2
Abbiamo eseguito un integrale immediato (QUI), del tipo:
∫ x dx = x2/2 + c
Non ci resta, adesso, che introdurre la nuova definizione di quantità di moto e vedere come si trasforma l’energia cinetica di un corpo che parte da fermo e arriva alla velocità v.
∫0s F ds = ∫0s (dq/dt) ds = ∫0s (d(m0γv)/dt) ds = ∫0t (d(m0γv)/dt) v dt …. (1)
Dobbiamo perciò calcolare l’integrale nel tempo della funzione:
P(t) = F v = v d(m0γv)/dt …. (2)
Non l’abbiamo chiamata P(t) a casaccio. Essa è proprio la potenza meccanica, ossia il lavoro compiuto nell’unità di tempo. Infatti:
P = dL/dt = F ds/dt = F v
Tuttavia, è inutile entrare nei dettagli, dato che il nostro scopo è ben altro.
La (2) non ci piace tanto come funzione di cui calcolare l’integrale. C’è una bella derivata già pronta, ma c’è anche una v sola soletta. Niente paura! Andiamo a recuperare un quiz che avevamo proposto poco tempo fa (QUI) con la relativa soluzione (QUI).
Riassumendo, era stato dimostrato che:
v·d(γ·v)/dt = c2· dγ/dt
Moltiplichiamo entrambi i suoi membri per m0 (costante) e otteniamo:
m0v·d(γ·v)/dt = c2· m0·dγ/dt
Magnifico! Possiamo allora inserire questa funzione all’interno dell’integrale (1)
∫0t m0 (d(γv)/dt) v dt = ∫0t c2· m0 (dγ/dt) dt = c2· m0 ∫0t (dγ/dt) dt
Quasi per miracolo, ci troviamo di fronte all’integrale di una derivata e quindi la sua soluzione è immediata (l’integrale è quella funzione la cui derivata è proprio la funzione da integrare):
K = ∫0s F ds = c2· m0 ∫0t (dγ/dt) dt = c2· m0 (γ(t) – γ(0)) = c2· m0 (γ(t) -1)
Ricordiamo, infatti, che (per t = 0, abbiamo v = 0)
γ(0) = 1/(1 – v2/c2) = 1/(1 – 0) = 1
Ancora un passaggio e …
K = c2· m0 γ - c2· m0 = m c2 – m0 c2 …. (3)
Dove m è la massa relativistica.
Ribadiamo subito un fatto fondamentale che abbiamo già toccato precedentemente. La massa relativistica m tende ad infinito per v che tende a c. Ne consegue che l'energia cinetica di un corpo di massa diversa da zero tende a infinito.
In altre parole: per fare acquistare una velocità pari a c a un corpo di massa a riposo non nulla, sarebbe necessario fornirgli un'energia infinita (ricordiamo che per ottenere energia cinetica è necessario far compiere lavoro a una forza). Questo è il motivo FISICO per cui la velocità della luce rappresenta una velocità limite per qualunque corpo materiale.
Ci torneremo ancora sopra (e come), ma possiamo dire che l’energia cinetica relativistica non è altro che la differenza di due energie (le unità di misura tornano perfettamente). Non fatevi ingannare dal fatto che non vedete la velocità espressa apertamente: essa è compresa nella massa relativistica m.
Assumendo come energia totale E di un corpo in movimento la quantità mc2 (deve essere un’energia da come è stata trovata!) si ha:
E = m c2 = m0 c2 + K
L’energia totale di un corpo è data dalla somma di due termini. Il primo è l’energia del corpo quando è in quiete, il secondo è la sua energia cinetica. In altre parole, anche se il corpo resta fermo (K = 0), esso possiede comunque un’energia che dipende soltanto dalla sua massa a riposo (moltiplicata per una costante). Non confondiamola con l'energia potenziale gravitazionale, mi raccomando! Non abbiamo nessun campo gravitazionale...
Ripetiamo ancora un risultato fondamentale per tutta la fisica: Un corpo in quiete possiede una certa energia a riposo (E0) e questa è data proprio dalla sua massa a riposo (a meno di una costante moltiplicativa):
E0 = m0c2
La vera legge relativistica rimane, comunque:
E = mc2
In cui la massa è funzione della velocità (ricordiamolo sempre!)
Massa ed energia sono la stessa cosa! Questa conclusione è ancora più evidente se decidiamo di misurare il tempo in metri-luce (ricordate?). In questo caso, come abbiamo visto nella RR, la velocità della luce diventa un parametro senza dimensioni ed è uguale all’unità. Ossia:
E = m
Guardiamola bene e ammiriamola in silenzio: questa semplice formula è un risultato mostruosamente importante per tutta la fisica moderna. E l’abbiamo ricavata con ben poca difficoltà (esistono anche altri metodi, alcuni dei quali apparentemente più semplici, ma troppo legati alla matematica e si perde il senso fisico che abbiamo mantenuto passo dopo passo).
Se ne potrebbe discutere per ore e si scoprirebbero infinite conseguenze fondamentali per tutti i campi della Scienza (chimica, termodinamica, fisica nucleare, …), senza escludere -purtroppo- nemmeno quello militare. Qualcuno la studieremo in dettaglio, ma ormai siamo in grado di capire tutto ciò che leggeremo a riguardo. Le basi sono state fissate e quello che serve è solo passione e applicazione.
Cari amici, ci siamo finalmente arrivati. E’ sempre una bella soddisfazione non prendere la formula come una specie di etichetta misteriosa, ma vederla comparire attraverso la logica.
Notiamo subito una cosa poco scientifica, ma molto indicativa: la sua semplicità! Si può dedurre con metodi più o meno facili (almeno per il nostro cervello), ma quando appare, sembra addirittura misera e ovvia. Tutto lì? Ebbene sì. Non c’è scritto da nessuna parte che la Natura debba usare formule complicate per costruire le sue leggi. Anzi, più le formule diventano semplici e più si può essere sicuri di essere vicini alla verità.
Va poi aggiunta una considerazione spesso trascurata, che abbiamo già ”toccato”. Einstein non l’ha dedotta casualmente alla fine di tanti calcoli laboriosi. Lui ne ha subito avuto l’intuizione e tutte le formule sono praticamente servite a confermarla e a legarla alle altre leggi fisiche, senza realmente distruggerne nessuna. Uno dei punti cardini della sua teoria è conservare i risultati di Newton per velocità “normali”. Quanti scienziati odierni avrebbero agito in questo modo? Basta vedere le idee rivoluzionarie che, pur basandosi sul niente, cercano prima di tutto di far crollare i pilastri portanti… poi si vedrà.
Non so se Einstein sia stato una persona con turbe emotive e nemmeno mi interessa la sua vita privata. So soltanto che Galileo, e lo stesso Newton, gli avrebbero stretto la mano!
Questa formula è sicuramente la più famosa, anche se porterà a qualcosa di ancora più eccezionale. E’ mai possibile? Sì, dato che attraverso una semplice uguaglianza ricaveremo nientemeno che un nuovo invariante relativistico, qualcosa che non cambia cambiando il sistema inerziale (vi ricordate la “distanza” spaziotemporale s2? In caso negativo, andate a rileggere questo articolo). Quello che sembra già un capolavoro può perfino essere superato!
Torniamo con i piedi per terra e lasciamo da parte (si fa per dire) l’emozione.
Questo fantastico abbraccio tra massa ed energia fa sì che quando si tratti con particelle estremamente piccole si preferisca (e sia più conveniente) esprimere la massa in termini di energia. In particolare si usa l’elettronvolt (eV) o, più comunemente, il suo multiplo (106) megaelettronvolt (MeV). L’elettronvolt rappresenta l’energia acquistata da un elettrone che viene accelerato da una differenza di potenziale di un volt. Tanto per fare un esempio, ricordiamo che la massa a riposo dell’elettrone è uguale a 0.511 Mev.






16 commenti
cari amici,
ho tolto dall'EVIDENZA gli articoli di dinamica relativistica precedenti... Li potete trovare facilmente cercando proprio "dinamica relativistica". Buona lettura... QUESTO è l'articolo che ci regala la celebre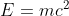 ... Non perdetelo...
... Non perdetelo...
Se trovate i miei soliti errorini ditemelo subito!!!!
ottimo percorso che ci ha condotti fin qui per mano e ottima conclusione anche se non definitiva . Grazie.
grazie Umberto... ma adesso che l'abbiamo raggiunta ci divertiremo un po' con lei
non ho dubbi..quell'invariante già mi incuriosisce..
Brian Greene, professore di fisica e matematica alla Columbia University, intervistato al Late Show di Stephen Colbert, spiega in maniera semplice e divertente il funzionamento delle onde gravitazionali. (I sottotitoli in italiano sono della community web Italiansubs).Scusate il fuori tema,oggi ho scoperto un video sul giornale La Stampa on line veramente papalliano e divertente,se qualcuno ha voglia di guardarlo...
Grazie per il consiglio, Gianni, ci puoi dare il link per favore?
P.S.
Anche se senza "foto", sono io che ho commentato...
Caro Enzo, quando ho iniziato a leggere i tuoi articoli sulla Relatività Ristretta, ne avevo solo una vaga idea, pochi concetti general generici sullo spaziotempo, sulla sua curvatura..
Ora, articolo dopo articolo ci hai portato fino ad una formula tanto conosciuta nella sua declinazione, quanto sconosciuta nella sua costruzione.
Un viaggio attraversato la fisica accompagnati dalla logica e dalla matematica, tra tempi e lunghezze non più assoluti, ma relativi, in cui l'unica cosa che rimane assoluta è la luce con la sua velocità costante uguale per qualunque sistema di riferimento.
Abbiamo dovuto irrobustire la matematica, arrivando fino agli integrali, ma la soddisfazione di essere arrivati a determinare la famosa formula penso che compensi lo sforzo, soprattutto di chi come te ha dovuto rendere tutto questo percorso comprensibile, anche a chi come me è partito con poche idee e piuttosto confuse..
Un grosso Grazie!
Paolo
caro Paolo, tu non sai quanto mi rendi felice...
è stata un esame importante anche per me e sono felice di essere riuscito a svolgerlo in collaborazione con voi. L'importante è che si capisca la meraviglia del Cosmo e che la matematica abbia rivestito il suo ruolo fondamentale di tradurre la meraviglia in una lingua comprensibile a tutti.
Pensate, cari amici, siamo riusciti attraverso quella mente semplice e universale di Einstein a descrivere i movimenti e la vita intera di quelle particelle che ancora adesso facciamo fatica a pensare, ma che regolano tutto l'Universo. La RR è una vera opera d'arte, un romanzo, una sinfonia: la puoi rileggere quanto vuoi e ti sorprenderà sempre.
Grazie a te e tutti gli altri che non hanno ceduto e ora possono gustarsi la semplicità e l'ovvietà dei risultati...
Se socchiudete gli occhi e ripensate anche alla QED, vi sembrerà di vedere agitarsi ovunque quei nostri amici così piccoli ma sempre così gioiosi ... La Natura ci apparirà diversa... e anche i valori e l'importanza dell'homo sapiens sapiens ...
Ciao Daniela,il video l'ho guardato nella pagina del quotidiano "La Stampa" di ieri è sottotitolato in italiano e dovresti trovarlo senza problemi,ci sono molti video di carattere scientifico come in tutti i giornali, anche precedenti.In alternativa lo trovi in you tube ma solo in Inglese si chiama"Gravitational Waves hit late show". Spiega con un modellino dell'interferometro LIGO funzionante come hanno registrato il fenomeno.
Grazie, Gianni, lo cercherò senz'altro!
Ciao Enzo,
innanzitutto grazie del fantastico e tanto atteso articolo! Ho seguito i passaggi nei due casi "classico" e "relativistico", dove ottieni:
per quanto riguarda il caso classico, e:
per il caso relativistico. Ho però difficoltà a conciliare le due espressioni per piccole velocità, dove mi aspetterei che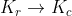 . Detto altrimenti mi aspetterei che
. Detto altrimenti mi aspetterei che 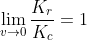 ma non mi sembra che sia così... ho provato a svolgere i calcoli, perdendomici un po' tanto che mi sono chiesto se questo calcolo avesse significato, ovvero se abbia senso fisico cercare un paragone tra
ma non mi sembra che sia così... ho provato a svolgere i calcoli, perdendomici un po' tanto che mi sono chiesto se questo calcolo avesse significato, ovvero se abbia senso fisico cercare un paragone tra 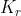 e
e 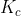 ...
...
caro Mik,
il tuo dubbio e la tua voglia di trovare la versione classica... ti fa onore! Innanzitutto, perché non hai perso di vista uno degli scopi di Einstein (mantenere Newton per velocità piccole) e poi perché -giustamente- ti trovi un po' sbilanciato... La prossima puntata è proprio dedicata al tuo problema e alla tua domanda. Una riprova che hai capito perfettamente tutto ciò che abbiamo fatto fino ad ora! Ti posso solo dire che non è banalissimo, dato che abbiamo bisogno di utilizzare una serie...
Comunque grazie Mik per avere centrato un problema VERO al momento e al posto giusto! e tanti complimenti, sinceramente...
Eh che soddisfazione fare le pulci ad Einstein!! Attendo il tuo prossimo articolo intanto mi immergo nella parte finale di questo!
Ciao di nuovo! Al terzo passaggio matematico cambi due volte la variabile di integrazione (da ds a dt e da dt a uno stranissimo "dmv"). Inoltre quel dmv proviene dalla derivata della quantità di moto che si trasforma nell'infinitesimo di integrazione. Non dubito della correttezza del calcolo ma devo dire che questi passaggi spericolati mi lasciano al palo... personalmente ho sempre trattato dy/dx reverenzialmente come un simbolo e un tutt'uno, così come l'integrale, non mi verrebbe mai da "rimescolarli" in quel modo (cosa che ho visto fare anche altrove beninteso).
Sai Mik,
non sono giochi di prestigio... Vi sono variabili tra loro interconnesse. Manovrando le espressioni contenute all'interno dell'integrale si mettono in evidenza nuovi differenziali che indicano chi deve variare, intervallino per intervallino. Ne consegue che devono anche variare conseguentemente gli intervalli di integrazione. Sono solo manovre che non cambiano il significato dell'integrale. Posso usare il tempo e /o lo spazio, tanto so come sono legati e, perché no?, anche la v che è legata al tempo...