Categorie: Relatività
Tags: costanza velocità della luce paradosso quiz relatività ristretta
Scritto da: Vincenzo Zappalà
Commenti:31
QUIZ: il paradosso della costanza della velocità della luce ***
Preambolo
Stiamo per finire la dinamica relativistica (ancora tre articoli, più o meno). Dopo, con molta calma, inizieremo, la relatività generale, sperando di spingersi più in là possibile sia con la logica che con la matematica (senza pretendere troppo, però).
Fatto questo saremo in grado di discutere molto meglio i buchi neri e le deformazioni spaziotemporali. Diamo, comunque, tempo al tempo, senza voler correre troppo.
Ho pensato, perciò, di inserire di tanto in tanto qualche paradosso e/o quiz sulla RR che possa servire come ripasso e come test per la comprensione dei punti essenziali. Già vi prometto che tenterò di farvi fare un viaggio fino ai bordi dell’Universo Osservabile in soli 25 anni e senza superare la velocità della luce. Dovremo introdurre (forse) i numeri immaginari e/o, quantomeno, le funzioni iperboliche… Niente di straordinario, ma con le idee ben chiare sul diagramma di Minkowski.
Dopo avervi fatto venire l’acquolina in bocca (spero…) torniamo a qualcosa di molto più semplice che è collegato alla costanza della velocità della luce e che può considerarsi un paradosso fondamentale.
La soluzione del paradosso è, teoricamente, semplicissima per chi ha digerito bene la RR e nasce dal postulato di Einstein che dice che la luce ha la stessa velocità in tutti i sistemi di riferimento inerziali.
Il paradosso
Consideriamo due papalli (rosso, R, e blu, B) muniti entrambi di un orologio estremamente preciso. Essi si ritrovano in un punto dello spazio e sincronizzano perfettamente i loro orologi.
Lo scopo dell’esperimento che vogliono fare è cercare di smentire quello sbruffone di PapalEinstein che ha appena “deciso” che la luce si propaga alla stessa velocità in tutti i sistemi di riferimento inerziali, ossia in tutti i sistemi che si muovono con velocità relativa costante.
I due papalli accendono una lampadina al tempo t = 0 e guardano quello che succede. La luce si propaga come un onda circolare e, all’istante t = 1, si è notevolmente allargata. Non ci sono comunque dubbi: entrambi sono rimasti al centro dell’onda. D’altra parte occupano entrambi la stessa posizione della lampadina e non si sono mossi di un metro. Possono anche disegnare facilmente la situazione nella Fig. 1, dove lo spazio è il piano del foglio. L’onda luminosa si propaga ovviamente secondo cerchi sempre più larghi rispetto alla lampadina e ai due papalli, ma senza cambiare la situazione generale.
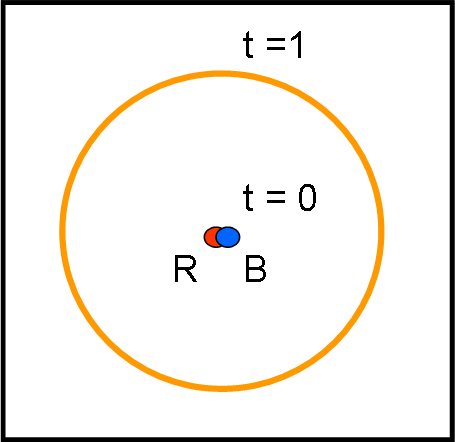
Fin qui tutto bene: PapalEinstein aveva ragione, ma il bello comincia adesso…
Lui parlava di sistemi inerziali e quindi il papallo blu, B, decide di muoversi rispetto al papallo rosso, R, con una velocità costante pari alla metà di quella della luce (i papalli possono fare questo e altro…).
Nello stesso momento in cui la lampadina si accende (t = 0), il papallo B, blu, inizia a muoversi verso destra con una velocità c/2. Se Einstein avesse ragione, la luce dovrebbe allontanarsi da lui con una velocità costante in tutte le direzioni, ossia lui dovrebbe continuare a stare al centro. Tuttavia, la stessa identica cosa dovrebbe dire anche il papallo R, rosso, che addirittura è rimasto fermo accanto alla lampadina.
Dopo che è passato lo stesso intervallo di tempo t = 1 per entrambi i papalli, essi gridano all’unisono: “Sono al centro dell’onda circolare luminosa, ma tu no! Enistein aveva torto”. PARADOSSO! In effetti, entrambi mostrano un disegno che vede loro al centro e l’amico di diverso colore nettamente fuori dal centro dell’onda.” Ciò si vede bene nelle Fig. 2a e 2b, eseguite dai due papalli.
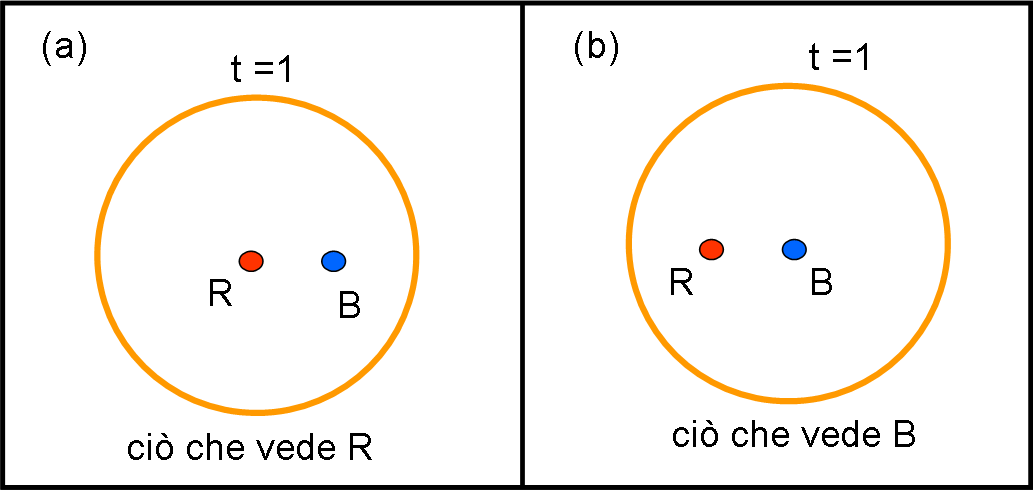
Ma lo stesso risultato è stato trovato da entrambi e, quindi, non appena hanno gridato, i due papalli si rendono conto, da ciò che urla l’amico, che Einstein aveva ragione: entrambi vedono la luce propagarsi alla stessa velocità, dato che entrambi si vedono al centro dell’onda.
Le figure 2a e 2b devono, perciò, essere sbagliate.
Come devono disegnare l’intera faccenda, all’istante t = 1, segnato dai loro orologi?
Si consiglia di fare una figura tridimensionale, per maggiore chiarezza, ma anche una bidimensionale (spazio rettilineo) può andare bene. La figura deve dimostrare chiaramente che entrambi i papalli, al tempo t = 1, sono al centro dell’onda luminosa che si propaga. Insomma, deve dimostrare che Einstein aveva ragione. Il Paradosso non esiste e noi abbiamo capito sempre meglio come funzione la RR e il diagramma di Minkowski. La soluzione è quassi solamente grafica...
Ho posto come difficoltà 3 asterischi, pensando a un lettore che abbia digerito abbastanza bene la RR. Invito veramente molti a provare, senza paura. Sbagliando si impara, non si fa mai brutta figura!
Spero di avere spiegato bene il paradosso… se ci sono problemi fatemelo sapere!
La soluzione la potete trovare QUI
31 commenti
Premesso che la mia digestione della RR è ancora in corso , mentre lo spazio di Minkowski ho appena iniziato a gustarlo.. :-) , un primo mio approccio al quiz è il seguente. A lume di logica direi che, necessariamente, dopo un tempo t i due papalli non posso stare fisicamente nello stesso posto, se B si muove verso destra con velocità pari a c/2. Quindi nelle due figure, le mutue posizioni di A e di B non sono sbagliate. Anche le due circonferenze , rappresentando l'onda di luce così come vista da ciascuno dei due papalli e sulla base del principio che c è costante in entrambi i sistemi di riferimento, non mi pare siano sbagliate. Quello che cambia dovrebbe essere la circonferenza di B così come vista da A e viceversa, circonferenze che pero' nelle due figure mancano.
Caro Enzo ho alcune domande da porre sul quiz ed in particolare su come interpretare la figura 2.
Nella figura viene indicato un generico tempo t=1, ma i due papallini si allontanano ad una velocità relativistica, quindi ogni orologio ha il suo tempo proprio, ossia t=1 è diverso da t'=1 ed anche la misura delle lunghezze cambia, ossia x=1 è diverso da x'=1.
Quindi la figura si riferisce a ciò che segnano i due orologi, oppure a ciò che segna l'orologio di uno dei due papallini?
La figura 2 rappresenta due immagini visive viste rispettivamente da ognuno dei due papalli, oppure la posizione spaziotemporale dell'altro papallo e della luce?
Provo a spiegarmi meglio: se un papallo dista 0,5 anni luce dall'altro, per vedere la sua immagine devo attendere 0,5 anni.... se invece ho un amico papallo che si muove alla mia stessa velocità (direzione e verso compresi), il cui orologio è sincronizzato con il mio, che si trova al tempo t=1 nella stessa posizione dove passa l'altro papallo, allora nella figura posso indicare secondo il mio sistema di riferimento la posizione dell'altro papallo.
In ultimo, è possibile rappresentare tutto con un diagramma spaziotemporale (alla Minkowski) , oppure bisogna realizzare una figura con assi X, Y e Z fissati a un'istante t misurato dal ogni sistema di riferimento?
Grazie per le delucidazioni
Paolo
scusate, al posto di "A" volevo dire "R".
Per maggior chiarezza, sostituirei l'ultima frase in verde con la seguente:
poiché è indifferente quale, tra R e B, sia considerato fermo e quale in movimento, entrambi i casi sono validi, con il risultato che sia R che B possono trovarsi in P=1, ovvero al centro dell'onda di luce e la vedono propagarsi alla stessa velocità
Posso dire che l'orologio di ciascuno è stato sincronizzato con l'altro alla partenza. poi... ognuno misura la sua ora (nel testo si dice: lo stesso intervallo di tempo per entrambi i papalli).
Per Arturo, le figure sono sbagliate nel senso che ognuno vede il compagno fuori centro. Solo in quel senso...
L'importante è fare una figura che spieghi la situazione reale, in cui si veda la circonferenza dell'onda di luce che deve essere unica in quanto parte da un solo punto. Ogni papallo può vedere solo un'onda circolare di luce a un dato tempo t.
In un certo senso posso anche dire che non sono sbagliate, ma da alcune cose scritte direi che sono sbagliate...
vi chiedo solo una figura a tre dimensioni (lo spazio è il piano del foglio a due dimensioni) in cui si veda la situazione di entrambi i papalli rispetto all'onda di luce partita da R=B(t = 0) che deve essere una sola per definizione. Va bene anche a due dimensioni, ma non è così difficile passare a tre...
Anche Dany dovrebbe spiegarsi un po' meglio...
Sto girando in tondo, ma è bene ripensare a queste cose...
le origini dei due sistemi di riferimento R e R' rosso e blue
sono sempre al centro del cono di luce grigio
Io sono un lettore silenzioso (molto); tuttavia in passato ho risposto qualche volta ma poi la mancanza di tempo e problemi vari mi hanno impedito di continuare a partecipare.
Questa volta voglio fare uno strappo alla regola e voglio provare a risolvere il quiz.
Premesso che non sono sicuro di aver capito bene la domanda di Vincenzo, soprattutto quando parla di figura tridimensionale (???), e che le mie basi sulla RR sono quelle che sono, proverei a disegnare un classico diagramma di Minkowski.
Per primo trovo le scale usando l’iperbole di calibrazione:
http://www.webalice.it/lottisimone/quiz%20luce%201.jpg
Poi provo a disegnare il caso specifico del quiz:
http://www.webalice.it/lottisimone/quiz%20luce%202.jpg
Si dovrebbe vedere che in entrambi i sistemi la luce si propaga sempre alla stessa velocità.
Quindi sia R che B si credono e lo sono, al centro della sfera di propagazione della luce (in questo caso è disegnato solo un asse, la x).
Ovvero per R, quando il suo orologio segna T=1, la luce è arrivata in x=1.
Per B, quando il suo orologio segna T’=1, la luce è arrivata in x’=1.
Quello che R e B non concordano è il tempo segnato dall’altro orologio, a causa della diversa simultaneità degli eventi.
Per R, a T=1, B si trova a x=0.5, ma il suo orologio non segna 1 ma T’=0.87.
Viceversa quando B segna T’=1, dal suo punto di vista, R segna T=0.87 e si trova a x’=-0.5.
Tra l’altro si nota la perfetta simmetria dei due sistemi, esattamente come dovrebbe essere, dato che non esiste un sistema privilegiato, essendo un moto a velocità costante o, meglio, rettilineo uniforme.
Spero di non aver fatto errori grossolani.
Ciao.
..Mah io ho provato a disegnare questa figura...
Paolo
mi fareste vedere più spessa la circonferenza (l'onda circolare della luce al tempo unitario ) vista da R e B? Tanto per essere sicuro...
Sono curioso di sapere come alla fine vanno modificate le figure 2a e 2b perché siano corrette. Poiché una delle basi della RR è che le leggi fisiche sono le stesse in tutti i sistemi di riferimento inerziali, se B si muove a velocità c/2 rispetto a R, è impossibile che R e B restino fisicamente nello stesso punto. E non posso avere una stessa circonferenza con il centro in due punti fisicamente diversi. La circonferenza vista da B, centrata in B ma riferita in R avrà raggio 0,87 ct. La circonferenza vista da R, centrata in R e riferita sempre in R, avrà raggio ct. Discorso speculare per B. Se sbaglio, dove sbaglio ?
occhio alle unità di misura... ogni figura ha le sue!
Vediamo se ho capito...
Usando le unità di misura ricavate nella figura precedente (Diagramma di Minkowski), ogni sistema misura tempo e distanze con il proprio sistema di riferimento.
Visto dal Papallo Rosso: quando il suo orologio segna t=1, il papallo Blu dista x=0,5, mentre la luce si è propagata in x=1 e -1; y= 1 e -1; z =1 e -1.
Visto dal Papallo Blu:: quando il suo orologio segna ti=1, il papallo Rosso dista
x'= -0,5, mentre la luce si è propagata in x'=1 e -1; y'= 1 e -1; z' =1 e -1.
... ma forse non è questo quanto richiesto dal quiz...
Paolo
Utilizzo la figura di Paolo per evidenziare le circonferenze (che nello spaziotempo bidimensionale di Minkowski diventano dei segmenti) rappresentative dell'onda di luce come vista da R e da B. La maggiore ampiezza della circonferenza vista da B è solo apparente.
Resto curioso di sapere cosa va corretto nelle figure 2a e 2b del quiz. Mi sembra pacifico che, al tempo t=1, R non possa vedere accanto a sè B e viceversa. Cioè , nel disegno eseguito da ciascun papallo, al centro dell'onda di luce non può metterci, oltre a sè stesso, anche l'altro papallo, perchP questi nel frattempo è corso via a velocità c/2 quindi fisicamente non lo vede più... . E allora, dove metterlo l'altro papallo nel disegno ? :-)
Non posso disegnare anche l'asse del tempo, però si può scandire il tempo per frazioni di 0,2 t :
Visto dal Papallo Blu con tempo scandito a intervalli di t'=0,2
Non so se son giuste, percò così le figure mi sembrano più chiare
Paolo
Nella prima immagine considero fermo R, nella seconda considero fermo B.
Provo a dire la mia in forma algebrica. Non sono riuscito a trovare per tutti i passaggi l'equivalente grafico.
Cerco di dimostrare che B vede allontanarsi da se a velocità c sia i raggi che R vede allontanarsi lungo l'asse x sia quelli che vede allontanarsi lungo l'asse y. Quindi sia R sia B, nei rispettivi riferimenti si mantengono al centro dell'onda circolare.
Nel sistema di riferimento di R, B vede come simultanei gli eventi sulle rette parallele a t=v x (utilizzando le unità di misura dove c=1).)
, sono per lui simultanei gli eventi su =v&space;(x-x_B))
nelle coordinate di R.
Quindi, quando B si trova in un punto
Nello stesso sistema di riferimento la luce viaggia sul cono che interseca il piano t-x nelle rette t=x e t=-x. Questa due rette intersecano la retta degli eventi simultanei per B in :
)
)
Nel sistema di riferimento di B questi punti corrispondono alle coordinate
Sostituendo x e t con i valori trovati sopra ottengo che:
Per la dilatazione dei tempi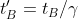
quindi 
, cioè B vede esattamente allontanarsi da se la luce alla stessa velocità vista da R, cioè 1.
Cosa accade per il raggio che si allontana sull'asse y?
In questo caso in R la luce segue le rette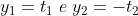
mantenedosi su x=0.)
è simultaneo l' istante =t'_B/\gamma)
su entrambe i raggi.
Ragionando come sopra trovo che per B in
Quindi la loro coordinata y per B sarà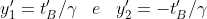
e la coordinata x sarà 
.
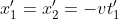Di conseguenza la loro distanza da B vista da B sarà}=t'_1&space;\sqrt{(1-v^2+v^2)}=t'_1)
e lo stesso per 
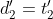, cioè la luce si allontana da B nel suo riferimento ad una velocita uguale ad 1 anche in questa direzione.
Ricapitolando sia i raggi che R vede allontanarsi lungo l'asse x sia quelli che vede allontanarsi lungo l'asse y, B li vede allontanarsi da se a velocità c mentenendosi quindi al centro tra di essi.
Per un generico raggio che segue una retta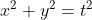
per R, credo si possa fare un ragionamento analogo solo un poco più complesso algebricamente.
I papalli (O e O')sono sempre al centro dell'onda; lo spaziotempo del blue è inclinato rispetto allo spaziotempo del rosso per mantenere la costanza della velocità della luce. I due bordi blu e rosso delle elissi (cerchi in prospettiva 3 d) rappresentano i due fronti d'onda, che sono sezioni del cono di luce e sono superfici di simultaneità; chiaramente questo disegno è dal punto di vista del papallo rosso; nell'altro caso i colori si invertono
Nel mio disegno bidimensionale, la proiezione della circonferenza rappresentativa dell'onda di luce è il segmento parallelo all'asse x, avente come punto medio P=1 ed estremi i punti d'incontro con v=c e v=-c
OK Dany. Questa è una circonferenza... e l'altra?
L'ho capito durante il tragitto in bici casa-ufficio (potere dell'aria fresca!)... è la linea di simultaneità del papallo in movimento, inclinata rispetto a quella del papallo fermo: l'estremo destro sopra, quello sinistro sotto, ma il papallo che si muove si trova sempre nel suo punto medio. Spero di essermi spiegata...
Ottimo esercizio per rinfrescare e memorizzare certi concetti!! Grazie
Ok questa dovrebbe essere la mia immagine definitiva, disegnata rispetto ad R fermo:
Questo è il mio tentativo di mettere in una immagine come ho trovato che nei rispettivi sistemi di riferimento B ed R vedono la stessa cosa, cioè la luce allontanarsi da loro a velocità c in ogni direzione.
Per semplificare le formule utilizzo le unità di misura nelle quali c=1.
Il sistema di riferimento dell'immagine è quello di R. In questo riferimento B percorre la retta)
che è l'asse t' nel sistema di riferimento B. Quindi in un certo istante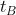 
, le coordinate di B saranno =(t_B,v&space;t_B,0).)
Nel sistema di riferimento di B, sono simultanei tutti i punti dei piani paralleli al piano definito dagli assi x' y', dove y' coincide con y e x' è la retta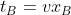
nel riferimento R. Quindi B vedrà come simultanei tutti i punti che nel sistema di riferimento di R sono sul piano=v&space;(x-x_B)=v&space;(x-t_B\,&space;v))
, piano blu in figura.
Le traiettorie dei raggi di luce partiti da=(t',x',y')=(0,0,0))
formano un cono i cui punti sono legati dalla relazione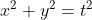 
(cono bianco in figura).
L'itersezione del piano detto sopra con il cono è quindi come B vede il propagarsi dei raggi di luce.
Nel riferimento R è una ellisse e non una circonferenza come per R, ma quello che interessa è come appare nel riferimento B.
L'asse minore (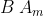
in figura) di questa ellisse è parallelo all'asse y che coincide con l'asse y'. Geometricamente è la corda di una circonferenza di raggio 
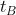a distanza 
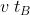dal centro. Con il teorema di Pitagora trovo che la lunghezza del semiasse è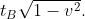 
L'asse maggiore ha come estremo (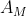
in figura) l'intersezione tra
=v&space;(x-t_B\:&space;v))
e la retta x=t sul piano y=0. Questo punto ha coordinate ,t_B&space;(1+v),0))
.
L'estremo opposto è sulla retta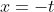
, e si trova nel punto di coordinate,-t_B&space;(1-v),0))
che è simmetrico rispetto a B.
B si trova al centro dell'ellisse nel riferimento R, ma quello che conta è il sistema di riferimento B.
A questo punto non ho trovato un modo rappresentabile direttamente sull'immagine per trovare la lungezza dell'asse maggiore nel riferimento B.
Un modo è quello di sfruttare l'invarianza della distanza quadridimensionale nel passare da un sistema di riferimento ad un altro.
La distanza tra,t_B&space;(1+v),0)\;&space;e&space;\;&space;\;&space;B=(t_B,v&space;t_B,0))
è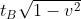 
questa distanza resta invariata nel riferimento B, dove i due punti sono simultanei. Quindi questa è la distanza spaziale tra i due punti e la lunghezza del semi-asse maggiore della nostra ellisse nel riferimento B.
Per esprimere tutto in coordinate di B, sostituisco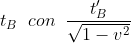
(dilatazione dei tempi) ed ottengo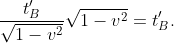 
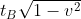da meno problemi poichè si trova sull'asse y, quindi non subisce contrazioni ed i suoi punti sono simultanei nei due riferimenti. In sostanza ha la stessa lunghezza nei due riferimenti. Anche qui sostituisco 
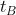con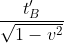 
. Quindi l'asse minore in B avrà lunghezza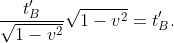 
L'asse minore di lunghezza
Quindi quella che in R sono ellissi in B sono circonferenze di raggio t'_B. In conclusione anche B vede allontanarsi la luce in ogni direzione a velocità c=1.
molto bella l'immagine Fabrizio; complimenti
facciamo il punto...
purtroppo i nomi sono sempre gli stessi... ma ... speriamo che molti altri si siano messi alla prova.
Il succo del paradosso era quello di introdurre in modo puramente grafico il diagramma di Minkowski, partendo da un apparente paradosso e da due figure che potevano sembrare sbagliate, ma che invece erano entrambe valide fatte le dovute trasformazioni grafiche. L'unica cosa di veramente sbagliato nelle figure era un unico tempo t, mentre doveva essere introdotto un t' per il papallo blu, visto dal papallo rosso.
Vorrei aspettare ancora un paio di giorni per vedere se qualcun altro si decidesse, magari, a uscire allo scoperto. Nel frattempo devo dire sia a Fabrizio (nessuna richiedeva le formule, ma comunque se serve come esercizio, fa sempre bene) che a Umberto che vi è un errore IMPORTANTE nelle loro figure, tenendo conto che si voleva la situazione allo stesso tempo per entrambi gli orologi dei due papalli...
Intanto, scaldate i motori... perché arriverà un nuovo quiz collegato a quanto abbiamo trovato, da risolvere solo graficamente e sul solito piano (x,t). Un quiz che costringerà a ricordarsi molto bene l'orologio a luce e il ... teorema di Pitagora. Nessun calcolo però... solo un collegamento logico e poi la risposta finale. La difficoltà sarà forse leggermente maggiore, ma il ragionamento è veramente banale (una volta scoperto il trucco...).
Purtroppo, il quiz sul viaggio ai confini dell'Universo non posso proporlo (bisognerebbero introdurre troppi concetti nuovi, che ci distoglierebbero troppo da problemi più fisici). Tuttavia, vi darò comunque i risultati, perché anche solo così, aiuta a capire la rivoluzione della RR fino ai suoi limiti estremi fantascientifici... Basta avere un motore e il viaggio si può fare ... facilmente.
è proprio quello che non riuscivo a capire del quiz quel t=1; io pensavo alla situazione vista da R ad un certo tempo (che poteva essere proprio t=1), cioè a un fotogramma determinato dallo spostamento fra i due sistemi (che a t=0 coincidono ma poi si allontanano) che poi risultava simmetrico visto dall'altra parte (t'=1). Qui invece bisognava considerare lo stesso tempo in sistemi diversi, sfalsando però i fotogrammi (traslando verso l'altro l'asse x' penso della figura) e riferendoci a fotogrammi diversi, propri dei due sistemi. Purtroppo non riesco ancora ad afferrare.
E' vero, ho ignorato l'indicazione sui tempi "numericamente" uguali nei due sistemi facendo il ragionamento per B simultaneo a R in R.
Perchè l'orologio di B segni un tempo uguale a quello di R, nel riferimento R devo fare avanzare B nel tempo di un fattore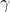
, conseguentemente il suo piano di simultaneità transla con B.
La figure diventa quella qui sotto che fa vedere meglio che B ed R vedono la stessa cosa.
Grazie Umberto per l'apprezzamento.
esatto Fabrizio...
Per Umberto: nella tua figura O e O' stanno sulla parallela all'asse x, ma questo vorrebbe dire che il tempo del rosso e quello del blu visto dal rosso sarebbero uguali... e invece sappiamo che non è vero (dilatazione dei tempi). L'unità di tempo lungo il percorso del blu (visto dal rosso) sta sulla famosa iperbole di calibrazione. Quando lo proietto sull'asse t (dove misura il rosso) il tempo di O' deve essere maggiore di quello di O.
Nel testo si dice che gli orologi in base ai quali i due papalli guardano la situazione sono i LORO orologi...
Forse non sono stato abbastanza chiaro su questo punto... t = 1 è il tempo proprio.
adesso ho capito: l'evoluzione del fronte d'onda rispetto ai rispettivi tempi propri. Io continuavo a pensare alla posizione di R' rispetto a R al tempo t=1 di R.
Non aggiorno il disegno, quello di Fabrizio mi sembra esteticamente migliore.
perfetto Umberto!
Sì, ci sono disegni ottimi e appena ho tempo (devo andare dal medico) pubblico la soluzione che sarà proprio uno di quei disegni.... e poi il nuovo quiz
A tempo scaduto cerco di completare il mio ragionamento sfruttando l'indicazione data da Enzo sull'utilizzo dell'iperbole di calibrazione in risposta ad Umberto. In effetti l'aveva già utilizzata Simone nella sua risposta.
Con l'iperbole di calibrazione posso trovare graficamente la lunghezza dell'asse maggiore dell'ellisse di propagazione della luce nel riferimento B che ero riuscito a trovare solo algebricamente con l'invarianza della distanza quadrimensionale. D'altra parte l'iperbole di calibrazione mi sembra la forma grafica di questa invarianza.
Reinserisco la vista totale ed il particolare dell'utilizzo dell'iperbole di calibrazione dell'asse x'.