La Dinamica Relativistica. 5: Quadrivettori, ancora Minkowski e un QUIZ … energetico ***/ *****

11/04/16

La Dinamica Relativistica. 5: Quadrivettori, ancora Minkowski e un QUIZ … energetico ***/ *****

Categorie: Relatività Tags: Scritto da: Vincenzo Zappalà Commenti:14

Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo

 

Anche chi non volesse cimentarsi con il QUIZ  (cinque asterischi) è comunque caldamente invitato a leggere questo articolo di impostazione e quello successivo di soluzione (tre asterischi) perché regalano ulteriori interpretazioni sulle formule che legano energia, massa e quantità di moto. Mettiamo in azione i cervelli! Forse pretendiamo troppo? Ma… chissà… In ogni modo, ci accorgeremo di quanto il diagramma di Minkowski possa diventare veramente uno strumento eccezionale.

Partiamo proprio da lontano, dalle trasformazioni di Lorentz, in cui scriviamo le coordinate di un evento visto da un sistema S’, che si muove con velocità u, rispetto al sistema considerato fisso S, lungo l’asse x. Le formule sono:

x’ = (x – ut)/(1 – u2/c2)1/2

y’ = y

z’ = z

t’ = (t – ux/c2)/(1 – u2/c2)1/2

Sappiamo che, scegliendo in modo acconcio le unità di misura, si può ottenere c = 1.

Risulta:

x’ = (x – ut)/(1 – u2)1/2

y’ = y

z’ = z

t’ = (t – ux)/(1 – u2)1/2

Noi avevamo posto T = ct (T’ = ct’), ma le cose non cambiano (nel caso, andatevi a rileggere le lezioni sulla basi della relatività speciale QUI) e continuiamo a scrivere t invece di T, pur considerando c = 1. E’ solo un problema di simboli…

Il tempo era diventato una coordinata del tutto simile a quelle spaziali ed eravamo passati dal concetto di punto al concetto di evento, definito da tre coordinate spaziali e da una temporale.

Avevamo poi dimostrato che la classica distanza tra due punti non si conservava nella relatività speciale, ma esisteva una speciale “distanza” che restava sempre la stessa in tutti i sistemi di riferimento (l’invariante spaziotemporale).

Lo avevamo chiamato s2 ed era stato definito come:

s2 = t’2 – x’2 – y’2 – z’2 = t2 – x2 – y2 – z2

Attraverso di lui Minkowski si era divertito a creare il suo Universo e molte altre cose.

Per maggiore chiarezza, noi avevamo solo considerato la componente x ( e x’) e la t ( e t’) in quanto lavoravamo solo nel piano x,t (x’,t’), ma il passaggio allo spaziotempo a quattro dimensioni è cosa più che intuitiva.

Cosa abbiamo fatto, in parole povere? Abbiamo associato a un vettore con tre componenti (in questo caso quello che definisce la posizione di un punto rispetto, ad esempio, all’origine) uno scalare che possiamo chiamare componente temporale. Questa grandezza a quattro dimensioni la chiamiamo quadrivettore. Come il vettore è rappresentabile con d(x,y,z) così il quadrivettore è rappresentabile con R(x,y,z,t).

Come per il vettore (chiamiamolo pure trivettore) la distanza d(x,y,z) definisce una distanza invariante nello spazio a tre dimensioni (cambiano le singole coordinate, ma non d2 = x2 + y2 + z2), così per il quadrivettore R(x,y,z,t) nello spaziotempo a quattro dimensioni si definisce  una “distanza” invariante s2 = t2 –x2 –y2 – z2. Quante interessanti riflessioni ci ha permesso di fare questa semplice “distanza” un po’ speciale (QUI)…

Esistono altri quadrivettori nello spaziotempo relativistico? Sicuramente sì. Uno lo abbiamo appena trovato ed è quello che ha come componenti quelle del vettore quantità di moto e come scalare l’energia.

In poche parole è un quadrivettore R(qx, qy, qz, E), così come quello spaziotemporale era R(x, y, z, t).

Scriviamo di nuovo l’invariante a lui associato:

E2 – q2c2 = costante

Imponiamo di nuovo, per analogia, che c sia proprio uguale a 1.

Allora, possiamo scrivere:

E = mc2 = m = m0/(1 – v2)1/2

E2 = m02/(1 – v2)

q = mv = m0v/(1 – v2)1/2

q2 = m02v2/(1 – v2)

Da cui:

E2 – q2 = m02/(1 – v2) - m02v2/(1 – v2) = m02(1 – v2)/(1 – v2) = m02

Ricapitoliamo:

E = m0/(1 – v2)1/2     …. (1)

q = m0v/(1 – v2)1/2     …. (2)

da cui l’invariante:

E2 – q2  = cost. = m02     …. (3)

Tra l’altro abbiamo anche una relazione poco usata ma molto interessante (anche se facile da ricavare):

q = E v        ….(4)

Non è difficile da interpretare. La quantità di moto relativistica è la massa relativistica moltiplicata per la velocità. Ma la massa relativistica non è altro che l’energia (avendo posto c = 1). Segniamocela, perché ci servirà nel quiz.

Il problema sollevato dal QUIZ è il seguente:

Semplifichiamo la situazione, come già fatto nella RR, e consideriamo un sistema S’ che si muova rispetto a S con velocità u lungo x, il che vuol dire che il sistema S si muove rispetto a S’ con velocità – u. La velocità u abbia la stessa direzione di v. Ciò vuol dire, in pratica, che possiamo considerare come quantità di moto solo la sua componente lungo questa direzione. Continuiamo a chiamarla q invece di qx, Valgono, perciò, le relazioni precedenti. Trascuriamo le componenti secondo x e y dato che non subiscono trasformazioni (e secondo qy e qz).

Vogliamo determinare le trasformazioni tra E e E’ e tra q e q’ (come fatto per t e t' e per x e x'). Ci accorgeremo che la loro scrittura diventa veramente immediata…

Ovviamente, bisogna anche verificare che:

E’2 – q’2 = E2 – q2

QUI trovate la soluzione

Articoli correlati

14 commenti

  1. Fabrizio
    11/04/2016 at 20:54

    Composizione delle velocità

    v'=\frac{-u+v}{1-u\cdot v}

    che va inserita nelle esoressioni di E' e q'

    E'=\frac{m_0}{\sqrt{1-{{v'}^{2}}}}\; \; \; \; \; \; \; q'=\frac{m_0 v'}{\sqrt{1-{{v'}^{2}}}}

    Calcolo separatamente i due fattori:

    \frac{1}{\sqrt{1-{{\mathit{v'}}^{2}}}}=\frac{1}{\sqrt{1-\frac{{{\left( v-u\right) }^{2}}}{{{\left( 1-u\cdot v\right) }^{2}}}}}=\frac{1-u\cdot v}{\sqrt{\left( 1-{{u}^{2}}\right) \cdot \left( 1-{{v}^{2}}\right) }}

    \frac{\mathit{v'}}{\sqrt{1-{{\mathit{v'}}^{2}}}}=\frac{v-u}{\left( 1-u\cdot v\right) \cdot \sqrt{1-{{\mathit{v1}}^{2}}}}={\frac{v-u}{\sqrt{\left( 1-{{u}^{2}}\right) \cdot \left( 1-{{v}^{2}}\right) }}}

    che inserite nelle espressioni di E' e q'  e sostituiendo le espressioni di E e q ricordate nell'articolo diventano

    E'=\frac{m_0}{\sqrt{1-{{v'}^{2}}}}=\frac{m_0}{\sqrt{1-{{u}^{2}}} \sqrt{1-{{v}^{2}}}}-\frac{m_0\; u\; \: v}{\sqrt{1-{{u}^{2}}} \sqrt{1-{{v}^{2}}}}=

    {\color{Red} E'=\frac{E}{\sqrt{1-{{u}^{2}}}}-\frac{u\; q}{\sqrt{1-{{u}^{2}}}}}

    q'=\frac{m_0 v'}{\sqrt{1-{{v'}^{2}}}}={\frac{m_0\: v-m_0\: u}{\sqrt{\left( 1-{{u}^{2}}\right) \cdot \left( 1-{{v}^{2}}\right) }}}

    {\color{Red} q'=\frac{q}{\sqrt{1-{{u}^{2}}}}-\frac{u\cdot E}{\sqrt{1-{{u}^{2}}}}}

    Trovata la relazione tra E' q' e E q sviluppo l'espressione che si dovrebbe conservare

    {{\mathit{E'}}^{2}}-{{\mathit{q'}}^{2}}=\frac{{{\left( E-q\cdot u\right) }^{2}}-{{\left( q-u\cdot E\right) }^{2}}}{1-{{u}^{2}}}=\frac{{{E}^{2}}+{{\left( q\cdot u\right) }^{2}}-\left( {{q}^{2}}+{{\left( u\cdot E\right) }^{2}}\right) }{1-{{u}^{2}}}

    {\color{Red} {{\mathit{E'}}^{2}}-{{\mathit{q'}}^{2}}={{E}^{2}}-{{q}^{2}}}

  2. Paolo
    12/04/2016 at 21:44

    Caro Enzo spero di aver capito poiché non mi è chiarissima la formulazione del quiz. :roll: 

    Io il problema lo inquadro così, sperando di non sbagliare: ci sono due sistemi di riferimento S ed S', il secondo visto dal primo si muove a velocità v... poi c'è un corpo in movimento di massa a riposo mo, che visto da S viaggia a velocità u e visto da S' viaggia a velocità u'.

    Per il sistema “fermo” S, ponendo c= 1, l'Energia e la quantità di moto del corpo in movimento sono uguali a:

    E = mo/√(1 – u²)

    q = mo u/√(1 – u²)...dato che mo/√(1 – u²) = E

    q= E u

    Per il sistema “in movimento” S', ponendo c= 1, l'Energia e la quantità di moto del corpo in movimento sono uguali a:

    E' = mo/√(1 – u'²)

    q' = mo u'/√(1 – u'²)

    Dato che i due sistemi di riferimento sono inerziali, ossia viaggiano a velocità costante e che il corpo si muove nella stessa direzione della velocità v di S' rispetto ad S, la composizione relativistica delle velocità riferita all'asse x è uguale a:

    u = (u’ + v)/(1 + vu’/c²)

    ma u' =-u; u= -u'; c² =1

    -u' = (-u + v)/(1 - vu)

    u' = (u - v)/(1 – vu)

    Prima di sostituire il valore di u' nelle equazioni precedenti per togliere di mezzo la radice quadrata elevo tutto al quadrato:

    E'² = mo²/(1 – u'²)

    q'² = mo²u'²/(1-u'²)

    u'² = (u - v)²/(1 – vu)² = (u ²+ v² -2vu)/(1+v²u² -2vu)

    E'² = mo²/(1 – u'²) = mo²/(1 – (u ²+ v² -2vu)/(1+v²u² -2vu)

    E'² = mo²/((1+v²u² -2vu) – (u ²+ v² -2vu))/(1+v²u² -2vu)

    E'² = mo² (1+v²u² -2vu)/(1+v²u² -2vu – u ²- v² +2vu)

    E'² = mo² (1+v²u² -2vu)/(1+ v²u² - u ²- v²)

    E'² = mo² (1+v²u² -2vu)/(1 – u ² -v² (1-u²))

    E'² = mo² (1+v²u² -2vu)/(1-u²) (1 -v²)

    ma (1+v²u² -2vu) = (1-vu)²

    E'² = mo² (1-vu)²/(1-u²) (1 -v²)

    se E = mo/√(1 – u²) ... E²= mo²/(1 – u²)

    E'² = E² (1-vu)²/(1 -v²)

    E' = E (1-vu)/√(1 -v²)

    E' = (E -Evu)/√(1 -v²)

    ma Eu = q

    E' = (E- qv)/√(1 -v²)

    L'Energia del corpo misurata dal sistema S' non è uguale a quella misurata da S.

    Ora tocca alla quantità di moto:

    q'² = mo²u'² 1/(1-u'²)

    q'² = mo²(u ²+ v² -2vu)/(1+v²u² -2vu) 1/(1- (u ²+ v² -2vu)/(1+v²u² -2vu))

    q'² = mo²(u ²+ v² -2vu)/(1+v²u² -2vu) (1+v²u² -2vu)/((1+v²u² -2vu)- (u ²+ v² -2vu))

    q'² = mo²(u ²+ v² -2vu) 1/(1+v²u² -2vu - u ²- v² +2vu)

    q'² = mo²(u ²+ v² -2vu) 1/(1+ v²u² - u ²- v²)

    q'² = mo²(u ²+ v² -2vu) 1/(1- u ²- v²(1- u²)

    q'² = mo²(u ²+ v² -2vu) 1/(1-u²) (1 -v²)

    ma (1+v²u² -2vu) = (1-vu)²

    q'² = mo² (u- v)²/(1-u²)(1 -v²)

    ma E²= mo²/(1 – u²)

    q'² = E² (u- v)²/(1 -v²)

    q' = E (u- v)/√(1 -v²)

    q' = (Eu- Ev)/√(1 -v²)

    ma Eu = q

    q' = (q - Ev)/√(1 -v²)

    Anche la quantità di moto del corpo vista da S' non è uguale a quella vista da S.

    Non resta che controllare se l'invariante è soddisfatta: E² – q² = E'² - q'²

    E' = (E- qv)/√(1 -v²).. quindi E'² = (E- qv)²/(1 -v²)

    q' = (q - Ev)/√(1 -v²),,, quindi q'² = (q - Ev)²/(1 -v²)

    E'² - q'²= (E- qv)²/(1 -v²) - (q - Ev)²/(1 -v²)

    E'² - q'²= (E- qv)²- (q - Ev)²/(1 -v²)

    E'² - q'²= (E² +q²v² -2Eqv - (q ² + E²v² -2Eqv)/(1 -v²)

    E'² - q'²= (E² +q²v² -2Eqv - q ² - E²v² +2Eqv)/(1 -v²)

    E'² - q'²= (E² (1-v²) - q² (1-v²))/(1 -v²)

    E'² - q'²= ((1-v²) (E² - q²)/(1 -v²)

    E'² - q'²= E² – q²

    Sembra che tutto funzioni... sempre che non abbia sbagliato l'impostazione. :roll: 

    Paolo

  3. Paolo
    13/04/2016 at 01:28

    Ho provato a trasformare e sintetizzare tutto in un grafico :roll: 

    Paolo

  4. Vincenzo Zappalà
    13/04/2016 at 05:51

    caro Paolo,

    non dico niente sul quiz, ma la figura potrebbe essere benissimo eseguita con le nuove coordinate, direttamente E e q... però non buttiamoci troppo avanti se no la gente scappa per davvero... :wink:

  5. Umberto
    13/04/2016 at 07:12

    Volevo provare vedendo come si trasforma in generale un vettore passando da un sistema di riferimento all'altro.

    chiamo L, I i due vettori unitari che si trovano sugli assi del primo sistema e L',I'. Uso le trasformazioni di Lorentz:

    t'=\gamma (t-ux)

    x'=\gamma (x-ut)

    ove \gamma =\gamma (u)=\frac{1}{\sqrt{1-u^{2}}}

    il vettore L' ha coordinate (0,1); basta sostituire e fare i calcoli per trovare le sue coordinate rispetto al primo sistema

    L'=\gamma uI + \gamma L

    infatti: x-ut=0; x=ut

    \gamma (x-u^{2}x)/u=1

    x(1-u^{2})/u=1

    x=u\gamma, t=\gamma

    allo stesso modo si ricava per I':

    I'=\gamma I + u\gamma L

    e invertendo:

    L=\gamma uI' - \gamma L'

    I=\gamma I' - u\gamma L'

    Passiamo al nostra problema; il vettore energia  può essere espresso nelle due basi:

    (applico lo stesso principio; in fin dei conti q=mV si trova anch'essa sull'asse spaziale in entrambi i riferimenti)

    E'L' + q I'=EL + qI

    Sostituendo le due espressioni nel secondo membro:

    EL + qI=E\gamma (L'-uI') + q\gamma (I'-uL')

    E'L + qI'=E\gamma L'-E\gamma uI'+q\gamma I'-\gamma quL

    eguagliamo le componenti dei due vettori:

    E'=E\gamma -\gamma qu

    q'=q\gamma -E\gamma u

    Il fatto che il modulo di questo vettore sia lo stesso nei due sistemi è dovuto proprio al fatto che è il modulo di uno stesso vettore

  6. Vincenzo Zappalà
    13/04/2016 at 09:51

    caro Umberto,

    devo dire che mi sono un po' perso... e non mi sembra molto legato al quiz.  Ma sarò io che non ho capito il procedimento (potresti spiegarlo con maggiore chiarezza? anche per gli altri lettori...).

    All'inizio parli di due vettori, ma in realtà esiste un solo vettore che è lo spazio (ridotto a x). Il tempo non è un vettore...

    E'L' + q I'=EL + qI

    da dove derivi questa uguaglianza... che è proprio quello che si deve dimostrare? Se vale questa è ovvio che valgono le relazioni finali di trasformazione...

  7. Umberto
    13/04/2016 at 11:23

    All'inizio parli di due vettori, ma in realtà esiste un solo vettore che è lo spazio (ridotto a x). Il tempo non è un vettore...

    Mi riferivo ai due vettori base dello spazio di Minkowski di cui hai parlato anche tu all' inizio dell'articolo; se un punto qualsiasi può essere espresso come un vettore dello spazio tempo, lo possono anche i punti (1,0) e (0,1) che sono dei vettori unitari. Ma noi possiamo esprimere con questi due vettori qualsiasi punto, tramite le componenti (coordinate). Poi con la trasformazione di Lorentz  ho espresso la relazione che lega i vettori di base dei due sistemi, sempre in Minkowski, vedendo come si trasformano i punti (1,0) e (0,1):

     

    L=\gamma uI' - \gamma L'

    I=\gamma I' - u\gamma L'

    per quanto riguarda il secondo punto,intanto c'è un errore di stampa; manca l'apice sul primo q:

    E'L' + q' I'=EL + qI intendo dire che il vettore nei due sistemi di  riferimento ha componenti diverse rispetto alle due basi (L',I') e (L,I), però il vettore è sempre lo stesso; sfruttando poi il legame fra le due basi (scusa se parlo di basi, ma non so se c'è un altro termine)

     

    L=\gamma uI' - \gamma L'

    I=\gamma I' - u\gamma L'

     

    EL + qI=E\gamma (L'-uI') + q\gamma (I'-uL')

    (anche qui c'era un errore mancava un apice su L)

    E'L + q'I'=E\gamma L'-E\gamma uI'+q\gamma I'-\gamma quL'

    eguagliamo le componenti dei due vettori (I,'L')

    E'=E\gamma -\gamma qu

    q'=q\gamma -E\gamma u

    comunque troppi errori, non si poteva capire in ogni caso, anche ammesso che sia giusto. In fin dei conti il quiz richiedeva come esprimere la trasformazione coordinate di E,q passando da un sistema all'altro, è per quello che ho seguito questa via, tanto come cercare come variano le coordinate x,t con la trasformazione di Lorentz

  8. Vincenzo Zappalà
    13/04/2016 at 11:38

    Caro Umberto,

    io non ha mai parlato di due vettori base nello spazio di Minkowski.

    L'unico vettore è lo spazio, definito da tre componenti (x,y,z) di cui noi ne prendiamo una sola (x) ed è quella che definisce il vettore. Per passare al quadrivettore bisogna aggiungere una quarta componente (nello spaziotempo a 4 dimensioni) che è però uno scalare (tempo).

    La distanza euclidea è data dal teorema di Pitagora applicato alle tre coordinate spaziali (relative al vettore spazio). Nelle 4 dimensioni dobbiamo costruire un invariante che deriva dal quadrivettore e che quindi lega indissolubilmente spazio e tempo.

    Comunque credo di aver capito cosa intendevi... (e penso sia anche abbastanza giusto), ma dovrebbe essere spiegato un po' meglio... :wink:

     

  9. Vincenzo Zappalà
    13/04/2016 at 15:16

    caro Umberto,

    la figura che hai fatto non mi torna...

    L'asse delle E è l'asse dello scalare che per c= 1 non è altro che la massa a riposo. Per cui si può descrivere, come fatto per il tempo, la curva di calibrazione, luogo dei punti per cui l'energia a riposo si conserva. Su ogni retta di velocità diversa puoi così trovare l'invariante che in questo caso è la massa a riposo del sistema considerato fermo. In questo contesto non capisco quella m0 vettoriale... Variando la velocità del sistema, la massa a riposo si dilata come il tempo se vista da E,q fermo. Idem per la q che segue ciò che faceva lo spazio x...

    Sempre che abbia capito bene la tua figura, ovviamente :-|

  10. Umberto
    13/04/2016 at 16:00

    no,per m0 intendevo il modulo, non una m0 vettoriale. La figura hai ragione può ingannare.

  11. Fabrizio
    13/04/2016 at 16:29

    Vorrei chiedere un chiarimento sul procedimento seguito da Umberto, in parte anticipato da Paolo.

    Mi sembra che si assuma in qualche modo che E e q siano le coordinate di un vettore quadridimensionale, in particolare che E sia analoga a t e q sia analoga a x, cosa che alla fine è probabilmente corretta.

    Da questa assunzione consegue direttamente che la trasformazione di E e q in E' e q' segue la stessa regola delle trasformazioni di t e x in t' e x'.

    Il mio dubbio è se si possa fare questa assunzione senza passare per una dimostrazione, che però credo porti al percorso inverso (magari partendo dal riferimento nel quale l'oggetto è in quiete): la coppia (E,q), si trasforma in modo analogo a (t,x) e quindi .......

     

     

     

  12. Paolo
    13/04/2016 at 22:21

    Sperando di non far scappare nessuno e soprattutto di non dire sciocchezze, ho provato a tracciare un grafico usando Energia e quantità di moto.

    Per tracciare gli assi e le relative unità di misura ho usato lo stesso metodo descritto qui

    Dunque sulle ordinate metto l'Energia E misurata dal sistema fermo e sulle ascisse la quantità di moto q misurata dal sistema fermo.

    Parto dalle relazioni trovate prima (sperando siano corrette):

    q' = (q - Ev)/√(1 -v²).... e...  E' = (E- qv)/√(1 -v²)

    la velocità v posso anche sostituirla con β, tanto c= 1

    q' = (q - βE)/√(1 -β ²)...  e... E' = (E- βq)/√(1 -β²)

    Per tracciare la retta che rappresenta l'asse E', pongo q'=0 (questo è il luogo dei punti che descrive l'asse E'):

    q' = (q - βE)/√(1 -β ²)

    0 = (q - βE)/√(1 -β ²)

    0 = (q - βE)

    q= βE

    1/β= E/q

    il coefficiente angolare della retta è il rapporto tra ordinate e ascisse (m=y/x), ossia m= E/q = 1/β

    Per tracciare la retta che rappresenta l'asse q', pongo E'=0

    E' = (E- βq)/√(1 -β²)

    0 = (E- βq)/√(1 -β²)

    0 = (E- βq)

    E = βq

    m= E/q = β

    A questo punto voglio vedere cosa misura l'asse E, quando E'=1.

    Si tratta di tracciare una retta parallela all'asse q', farla passare per E'=1 e vedere dove interseca l'asse E.

    Tale retta avrà quindi un'equazione tipo: y = mx + n.

    E' = (E- βq)/√(1 -β²)...... ma 1/√(1 -β²) = γ

    E' = (E- βq) γ = Eγ – βqγ

    E' + βqγ = Eγ

    E'/γ + βqγ/γ = E

    E = βq + E'/γ

    Questa è l'equazione della retta parallela all'asse q' rappresentata nel sistema fermo, y= mx + n, dove y= E; m=β (lo stesso coefficiente angolare dell'asse q'); x=q; e n= E'/γ.

    Quando E'=1 la retta passa per l'unità di misura dell'asse E': E = βq + 1/γ

    La retta interseca l'asse E, quando q=0 (luogo dei punti che descrive l'asse E)

    E = 0 + 1/γ

    Quando E'=1 l'Energia misurata dal sistema fermo è uguale a E= 1/γ

    Applicando lo stesso procedimento per trovare cosa misura l'asse q, quando q'=1, si ottiene:

    q' = (q - βE)/√(1 -β ²) = (q - βE)γ = q γ - βEγ

    βEγ = q γ - q'

    E = qγ/βγ -q'/βγ

    E = q/β - q'/βγ

    Questa è l'equazione della retta parallela all'asse E', dove y=E, m=1/β (lo stesso coefficiente angolare dell'asse E'); x= q; n=q'/βγ.

    Con q'= 1 e E=0 (luoghi dei punti che descrivono l'asse q')

    0 = q/β -1/βγ

    1/βγ = q/β

    1/γ= qβ/β

    q= 1/γ

    Quando q'=1 la quantità di moto misurata dal sistema fermo è uguale a q= 1/γ

    Se il ragionamento è corretto questo dovrebbe essere il grafico conseguente

    Ovviamente non so se questo ragionamento è corretto, oppure no... :roll: 

    Paolo

  13. Vincenzo Zappalà
    14/04/2016 at 05:56

    in realtà, non facciamo altro che sostituire x e t con q ed E, con tutte le conseguenze del caso sull'energia riposo e sulle relazioni tra E e q nelle varie zone...

    Direi, però, di non proseguire oltre, dato che si entrerebbe in un campo che si complicherebbe sempre di più...

    Temo che questi articoli vengano veramente letti solo da un manipolo (stanno su una mano) di lettori. Dobbiamo pensare anche agli altri e, direi, che la dinamica quantistica l'abbiamo sviscerata abbastanza.  Domani pubblico la soluzione e poi ancora un articoletto e completiamo la DR. OK?

  14. Fabrizio
    14/04/2016 at 09:47

    Aggiungo solo i miei due grafici che non ero riuscito a finire ieri sera.

    Parto dal riferimento (rosso) dove l'oggetto è in quiete ed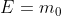  E=m_0

    Il riferimento blu  è quello dove è in moto a velocità v e -v. Qui E' e q' sono quelle della loro definizione ricordata nell'articolo riportate in forma grafica sugli assi t' e x' per la stessa v.

    Poichè in questi grafici v è arbitraria, si può dedurre che (E,q) si trasformano come (x,t).

    Si può anche vedere come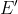  E' rimanga positiva indipendentemente dalla direzione di v, mentre q' cambia segno.

     

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.