Viaggiare verso Alpha Centauri si può (grazie alla quantità di moto)! **

15/04/16

Viaggiare verso Alpha Centauri si può (grazie alla quantità di moto)! **

Categorie: Fisica classica Relatività Stelle Strumenti e missioni Tags: Scritto da: Vincenzo Zappalà Commenti:11

Se ne sta parlando dappertutto e potrebbe sembrare la solita notizia mediatica da prendere con le molle. In realtà, in parte lo è e il nome di Hawking viene fatto per dare una valenza scientifica che è già ben conosciuta. Tuttavia, anche se ancora prematura come realizzazione, l’idea delle piccole vele solari è qualcosa di scientificamente valido. Vale la pena analizzarla un po’ più seriamente, dato che ultimamente  abbiamo parlato spesso di quantità di moto e di velocità della luce.

Diciamo subito che l’idea non è affatto nuova e le vele solari non sono soltanto  già state prese in considerazione da molti anni , ma anche applicate a una sonda giapponese. Si parlava sempre, però, di vele manovrabili da Terra ed enormi, per aumentare la superficie di raccolta dei fotoni. Riducendo la massa dell’astronave, però, l’applicazione può arrivare a limiti straordinari. Il propulsore sarebbe, ovviamente, la luce o se preferiamo il fotone, quella onda-particella costretta a muoversi continuamente per esistere e anche alla massima velocità possibile: trecentomila  chilometri al secondo.

Le piccole vele, con a bordo un microchip (che in pochi anni potrà anche ridurre la sua massa in modo significativo) verranno spinte dalla pressione di radiazione, un concetto già espresso e dimostrato da Maxwell, quando ancora la luce era vista solo come onda. Oggi, possiamo permetterci di parlare di fotoni, ossia di particelle che trasportano la luce (anzi sono loro la stessa luce).

Sappiamo che non hanno massa riposo, ma hanno massa relativistica e questo fatto comporta che abbiano anche una quantità di moto e una certa energia. Anzi, la quantità di moto q è proprio uguale all’energia E, ponendo c = 1. Sono cose che abbiamo già discusso varie volte, ma basta ricordare che l’energia relativistica è data da (vedi, ad esempio QUI):

E2 = c2q2 + m02c4

Nel caso del fotone la massa a riposo è uguale a zero e quindi:

E2 = c2q2

Ossia:

q = E/c

Se la formula vi sembra strana, ricordiamo che E = mc2, dove m è la massa relativistica. Da cui:

m2c4 = c2q2

q2 = m2c2

q = mc

proprio una massa moltiplicata per una velocità…

Fatti i doverosi richiami, occupiamoci della nostra astronave che possiamo considerare come una piccolissima vela quadrata V con una massa più piccola possibile. Immaginiamo di spararle contro un fotone (meglio molti fotoni) che trasportano ognuno la loro quantità di moto. Quella della vela è invece uguale a zero, dato che la consideriamo ferma.

Consideriamo il caso più favorevole, in cui ammettiamo che il fotone raggiunga la vela esattamente lungo la direzione perpendicolare. Non solo, però. Abbiamo anche costruito una vela con una superficie perfettamente riflettente, ossia il fotone che la colpisce torna esattamente indietro, ovviamente con velocità uguale e contraria. Cosa questa non certo facile da ottenere: la vela deve essere veramente speciale.

vela

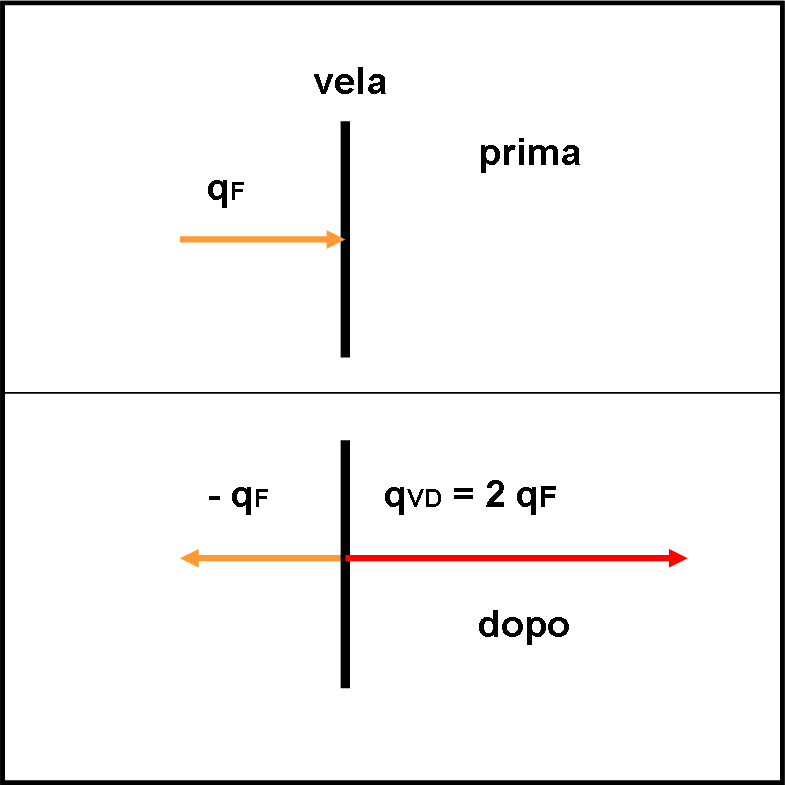
Prima dell’urto, la quantità di moto del sistema fotone + vela, qprima, è dato da:

qprima = qF + qVP = qF         (la vela è ferma)

con qF e qVP le quantità di moto del fotone e della vela prima dell’urto.

Dopo l’urto la quantità di moto deve essere:

qdopo  = - qF + qVD      (la quantità di moto del fotone cambia solo di segno, dato che il fotone torna indietro)

Per la conservazione della quantità di moto si ha:

qprima = qdopo

qF = - qF+ qVD

qVD = 2qF

qVD = mVvV  =  2qF            (con mV e vV la massa e la velocità della vela)

vV = 2qF/mV

La quantità di moto del fotone dipende dalla lunghezza d’onda e quindi dalla frequenza f secondo la celebre formula quantistica:

qF = hf/c

Dove h è la costante di Planck. Si ha, infine:

vV = 2hf/(c mV)

Facendo i conti, puramente teorici, ma sicuramente plausibili tra non molti anni, si pensa di poter raggiungere velocità dell’ordine di 1/5 di quella della luce. Così, almeno, dicono… e quindi arrivare sulla stella a noi più vicina in circa 20 anni.

Ovviamente, bisognerebbe essere molto precisi nell’invio del raggio laser contro le vele e tenere in conto che per uscire dal Sistema Solare si deve vincere la sua gravità (dove mettere le vele?). Ma, questi sono problemi che, al momento, interessano poco. In modo molto elementare, anche se semplificato, abbiamo capito che il merito è sempre della mia carissima amica, la quantità di moto.

Il tutto va trattato attraverso la dinamica relativistica, dato che le velocità sono piuttosto… alte!

Chi ha voglia i complicarsi un po' la vita (ma è esercizio facile) può considerare il caso più plausibile in cui il fotone arrivi sulla vela con un angolo non uguale a 90°. Come si trasformano le formule di prima (sempre ammettendo una riflessione perfetta)?

 

Per approfondire la conoscenza della quantità di moto (e non solo)

http://www.infinitoteatrodelcosmo.it/2015/07/29/il-nostro-amico-momento-angolare/

 

Articoli correlati

11 commenti

  1. luciano
    16/04/2016 at 16:22

    Mah... Una sola concentrazione di fotoni sparati dalla Terra contro tutti gli altri vaganti nell'Universo, ed in ultimo quelli antagonisti della stessa Alpha Centauri. Non sarà sufficiente sapere andare di poppa ma anche di bolina. Chi mettiamo al timone?

    E poi, anche ammesso che si riesca a produrre l'enorme energia necessaria a spingere la Vela e per un tempo così lungo, saranno tutti d'accordo gli abitanti della Terra a subire la relativa reazione? Bisognerà prima sopprimere i Verdi. :wink: .

  2. Paolo
    16/04/2016 at 17:36

    Nel caso di un'inclinazione tra fotoni e vela diversa da 90°, ho solo scomposto il vettore qF nelle sue due componenti (seno e coseno) rispetto all'angolo α e considerato solo la sua proiezione lungo il moto perpendicolare alla vela.

    Ovviamente se l'angolo α è di 90° il seno vale 1, mentre se l'angolo è di 0° la vela non “respinge” fotoni e la sua velocità non cambia.

    Paolo

  3. Paolo
    16/04/2016 at 17:50

    Gulp, scusate, forse così è più realistica....

     

  4. Fabrizio
    17/04/2016 at 10:28

    Ho provato ad interpretare l'ultima frase dell'articolo che ci ricorda che per le velocità della sonda occorre tenere conto della dinamica relativistica.

    Indico con v la velocità della sonda rispetto alla sorgente del laser e f la frequenza del laser.

    L'energia del fotone alla sorgente sarebbe EF=h f e la quantità di moto qF =EF  , in generale q=u E, ma per il fotone u=c=1.

    Quindi con le trasformazioni viste nel 5° articolo sulla dinamica relativistica la quantità di moto del fotone in arrivo nel riferimento della sonda sarebbe:

    qF '=(qF -v E)/(1 – v2)1/2=qF (1-v)/(1 – v2)1/2

    qF'=h f  (1-v)/(1 – v2)1/2

    Quindi la quantità di moto della sonda dopo l'urto sarebbe (prima è 0):

    q'SD=2 h f  (1-v)/(1 – v2)1/2

    ma q'SD=mS w/(1 – w2)1/2

    qui i passaggi si complicano dovendo ricavare w da questa equazione ed applicare la composizione delle velocità con v per ottenere la variazioni di velocità rispetto a terra.

    Ma forse si può considerare w<<1, in questo caso la variazione di velocità rispetto a terra sarebbe w=2 h f  (1-v)/(mS (1 – v2)1/2)

    Nel caso v=0.2 ipotizzato per la sonda, se non ho fatto errori, la variazione di velocità dopo l'urto con un fotone sarebbe:

    w≈0.82 2 h f/mS  (un poco meglio dell'0,8 non relativistico).

    Ma è corretto applicare queste trasformazioni a questo caso dove i due riferimenti sono in moto accelerato?

     

     

  5. Fabrizio
    17/04/2016 at 10:46

    Scusate, nell'invio è scomparsa la formattazione degli apici e dei pedici.

    Dove c'è (1 – v2)1/2 e (1 – w2)1/2 va letto (1-v^2)^{1/2} e (1-w^2)^{1/2}

  6. Vincenzo Zappalà
    17/04/2016 at 15:10

    caro Luciano,

    perché dici di sparare per un tempo lungo? La qm si conserva nello spazio. Basta sparare una volta e via... Ammetto, comunque che la faccenda è solo una teoria per adesso molto teorica...

    Caro Fabriio,

    per maggiore chiarezza dovresti fare una figura e spiegare bene cosa sono v , w e F'..

  7. Marco
    19/04/2016 at 13:44

    Ho guardato il video di Media Inaf (https://www.youtube.com/watch?v=ycTw2FTaCt8&list=UL), dove, al minuto 1:10-1:15 si dice che "In meno di 2 minuti le sonde percorrono qualcosa come 600.000 chilometri". Qualcosa non mi quadra.

    Se si parla del tratto iniziale, supponendo costante l'accelerazione e una velocità iniziale nulla, essendo s=1/2*a*t^2, e quindi a=2*s/t^2, ponendo s=600.000.000 m e t=120 s si ottiene a=2*600.000.000/120^2=83.333 m/s^2, che diviso g=9,8 m/s^2 diventa a=8.503 g: ottomilacinquecento volte l'accelerazione di gravità! Non è un po' troppo?

    Se, invece, si parla del tratto finale, in cui non c'è più accelerazione, e quindi il moto è uniforme, si ottiene v=600.000 km/120 s=5.000 km/s. Troppo poco, visto che si dice (nel video, e altrove) che queste sonde dovrebbero raggiungere 1/5 della velocità della luce nel vuoto, e quindi circa 60.000 km/s!

    Ma allora, come sono venuti fuori questi 600.000 km in meno di 2 minuti?

  8. Vincenzo Zappalà
    20/04/2016 at 15:12

    caro Marco,

    per come l'ho intesa io (e per come l'ho voluta presentare in modo puramente didattico), si tratta solo di un trasferimento di quantità di moto, per cui non vi è accelerazione. La vela si muove con velocità costante di 1/5 di quella della luce fin da subito dopo l'impatto con il fotone. Non so, però, se nei calcoli riportati dall'INAF si tenga conto dell'attrazione del Sole e di altri problemi di frenamento iniziale. E nemmeno si dice da dove fare partire la vela... Quindi sui numeri sareei molto dubbioso...

  9. Fabrizio
    20/04/2016 at 18:35

    Ascoltando le parti della conferenza di Yuri Milner e altri responsabili del progetto disponibili in rete non ho trovato neanche io alcun riferimento ai 600.000 km in 2s citati nel video INAF.

    Però, per quanto riguarda le accelerazioni, credo che quella prevista nel progetto possa essere dell'ordine di grandezza di quella che ha trovato Marco o anche più alta, se non ho fatto qualche confusione con gli ordini di grandezza.

    Parlano di raggiungere la "velocità di crociera" di 60.000km/s in pochi minuti.

    Se fossero 10 minuti, 600s, l'accelerazione sarebbe 100.000 m/s^2, se i minuti fossero 2 sarebbe 500.000 m/s^2.

    Con questi valori si avrebbero potenze nette trasferite alla sonda dell'ordine di grandezza del GigaW, dovendo raggiungere una energia cinetica di circa 400GJ in quei pochi minuti. Ho calcolato grossolanamete l'energia con la formula classica dell'energia cinetica per i 220mg, che ipotizzano per la sonda, E=0,5 m v^2=0,5 0,22 10^-3 (60 10^6)^2 J=396 10^9 J.

    Il valore di potenza detto sopra sembra coerente con il fascio laser di un centinaio di GW che hanno come obiettivo, considerando che il rendimento dovrebbe essere piuttosto basso.

    Caro Enzo,
    sto ancora cercando di preparare l'approfondimento che mi hai suggerito.
    Ho trovato qualche difficoltà che spero di avere superato. La principale ha proprio a che fare con il rendimento.

  10. Fabrizio
    05/05/2016 at 02:11

    Vorrei condividere un approfondimento che ho tentato di fare sul progetto descritto nell'articolo, sperando di non violare l'etichetta del blog proponendolo come commento.

    Seguendo il consiglio  di chiarire meglio quanto avevo detto piuttosto confusamente nel mio penultimo messaggio, ho esteso il mio obiettivo cercando di trovare quale dovrebbe essere la potenza del fascio laser, almeno nelle condizioni ideali di urto elastico e fascio perfettamente collimato ed in linea con la velocità della vela. E' stato più complicato di quello che pensavo, vediamo se ci sono riuscito.

    Anticipo il risultato.

    Dalla conservazione dell'energia e della quantità di moto prima e dopo l'urto ricavo la variazione di velocità della vela causata dall'urto di un fotone:

    \Delta v \simeq \frac{2 h f}{m_v} \left ( 1-v \right ) \sqrt{1-v^2}

    Dovrei sommare il contributo dei singoli urti che dipende dalla velocità della vela e questo complica l'operazione. Alla fine ho pensato di trattarlo come un integrale visto che i singoli contributi sono molto piccoli. così ho ottenuto l'energia totale necessaria per portare la vela alla sua velocità finale

    dv \simeq \frac{2\, dE_{laser}}{m_v} \left ( 1-v \right ) \sqrt{1-v^2} \newline \int_{0}^{E_{totale}} dE_{laser}=\int_{0}^{v_f}\frac{m_v} {2(1-v)\sqrt{1-v^2}} dv \newline E_{totale}=\frac{m_v}{2}\left [ \sqrt{\frac{1+v}{1-v}} \right ]_{0}^{v_f} =\frac{m_v}{2} \left [ \sqrt{\frac{1+v_f}{1-v_f}}-1 \right ]\newline

    Questo in unità relativistiche, per ritornare alle unità usuali  moltiplico per c^2.

    E_{totale}\approx \frac{220\: 10^{-6} {(3\: 10^{8})}^2}{2} \left [ \sqrt{\frac{1+0,2}{1-0,2}}-1 \right ]J\approx 2,22\, 10^{12} J

    La potenza del laser per accelerare la vela in 5 minuti sarà quindi:

    P_{laser}=\frac{E_{totale}}{T}\approx \frac{2,22\, 10^{12}}{300}J\approx 7,4\, GW

    Ovviamente nelle condizioni ideali dette sopra e se non ho fatto qualche errore.

    Nel mio ragionamento ho utilizzato due riferimenti, entrambe con gli assi x orientati nel verso del moto della vela:

    • il riferimento terrestre S, rispetto al quale sono riferite la velocità della vela e l'energia del fascio laser.
    • il riferimento S' che al momento dell'urto con il fotone ha temporaneamente la velocità della vela.

    Nelle prossime 2 immagini ho riportato le grandezze in gioco prima e dopo l'urto cercando di evidenziare le incognite ed alcune relazioni tra queste grandezze che ho utilizzato nel ragionamento.

    La decodifica dei pedici è f:fotone, v:vela, p:prima, d:dopo. La grandezze rosse senza apice sono riferite a S, il riferimento terrestre, quelle blu con apice al riferimento S',il riferimento temporaneamente solidale con la vela.

     

    e

    Nel cercare la soluzione più semplice ho tentato diverse vie, alcune scartate per la complessità dei calcoli, altre le ho portate fino in fondo. In tutte ho dovuto fare delle approssimazioni per arrivare ad un risultato.

    Il punto di partenza sono state la conservazione dell'energia e della quantità di moto prima e dopo l'urto. http://www.infinitoteatrodelcosmo.it/2016/02/07/dinamica-relativistica-1-cambiamo-la-quantita-di-moto-4/

    Avendo 3 incognite (quantità di moto del fotone dopo l'urto, energia e quantità di moto della vela dopo l'urto) ho dovuto anche aggiungere la relazione tra energia e quantità di moto relativistiche vista nel 4° articolo della dinamica relativistica http://www.infinitoteatrodelcosmo.it/2016/03/29/la-dinamica-relativistica-4-un-nuovo-invariante-relativistico-1/.

    Quando le espressione trovate sono diventate troppo complesse, le ho approssimate applicando lo sviluppo in serie di McLaurin http://www.infinitoteatrodelcosmo.it/2015/10/30/37-costruzione-rigorosa-della-formula-di-taylor-prima-parte/.

    Nello schema seguente c'è la traccia dei ragionamenti per arrivare alla variazione di velocita della vela a seguito dell'urto di un fotone.

     

     

     

     

     

  11. Vincenzo Zappalà
    05/05/2016 at 05:22

    caro Fabry,

    così a occhio mi sembra un ottimo lavoro, anche se forse va un po' oltre le pretese del blog. In questo periodo ho un po' il tempo contato... ma sono sicuro che altri del circolo avranno voglia di controllare il tutto... Una bella discussione tra i più attivi e stimolati del circolo. Io sto lavorando duro nel passaggio a Keplero e con problemini extra circolo e non vorrei distrarmi troppo... Dai che ti lascio in buona compagnia...

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.