Per una trattazione accurata degli urti elastici potete andare QUI (effetto Compton), ma ritroveremo le stesse formule partendo dagli urti anelastici in genere.

Ciò che caratterizza i vari tipi di urto è la legge di conservazione dell’energia cinetica. Essa  rimane valida solo nel caso di un urto completamente elastico. Non vi è conservazione in tutti gli altri casi di urto, in quanto una certa quantità di energia cinetica viene trasformata nell’urto in altre forme di energia (rumore, calore, deformazione, …). La dinamica relativistica, appena terminata, ci ha mostrato come si comporti l’energia totale e come si conservi sempre.

Il valore massimo di energia assorbita si ha quando l’urto è completamente anelastico. In questo caso si ha anche come risultato l’unione delle due particelle in gioco che possono proseguire insieme con una certa velocità. Se le due particelle si separano dopo l’urto (muovendosi ognuna con una certa velocità) abbiamo i vari casi di urto anelastico.

Dato che la differenza tra i vari tipi di urto si ottiene attraverso l’energia cinetica, si definisce un coefficiente di restituzione e, tale che:

E_CD = e²E_CP

Dove e può variare tra 0 e 1. Nel caso valga 0, siamo nel caso dell’urto completamente anelastico, mentre, se vale 1, siamo nel campo degli urti elastici.

In TUTTI i casi, comunque, deve valere la conservazione della quantità di moto. Ossia quella prima dell’urto deve essere uguale a quella dopo l’urto.

Un commento importante prima di iniziare. Niente ci vieta di considerare una delle due particelle ferma prima dell’urto. Tuttavia, non è assolutamente possibile considerare la particella IMMOBILE, dopo l’urto. Facendo questo, introdurremmo una forza esterna (un vincolo) che obbligherebbe la particella a non subire spostamenti. Ne seguirebbe che la conservazione della quantità di moto non sarebbe più verificata!

Normalmente, per descrivere un urto si utilizza un sistema di riferimento inerziale qualsiasi. Ciò, però, comporta una conservazione della quantità di moto del tipo:

m₁v_1P + m₂v_2P = m₁v_1D + m₂v_2D

dove i pedici P e D si riferiscono a prima e dopo l’urto.

La faccenda non dà grossi problemi, trattando urti completamente elastici e anelastici (come abbiamo visto quando li abbiamo descritti), ma può complicare le cose quando si descrivono urti anelastici in genere, dove compare il coefficiente e.

Conviene, allora, cambiare sistema di riferimento e trattare l’urto anelastico generico in un sistema di riferimento solidale con il baricentro (o centro di massa) del sistema delle due particelle. Per far ciò dobbiamo riferire le velocità delle due particelle in gioco al loro centro di massa. Ovviamente, il centro di massa si muove con una certa velocità, dato che cambia da istante a istante la configurazione del sistema.

Il grande vantaggio di questa scelta è quella di avere la quantità di moto totale prima e dopo l’urto sempre uguale a ZERO (come dimostreremo tra poco).

Per riferire le velocità al centro di massa, basta eseguire le seguenti operazioni vettoriali:

v’_1P = v_1P - v_B

v’_2P = v_2P - v_B

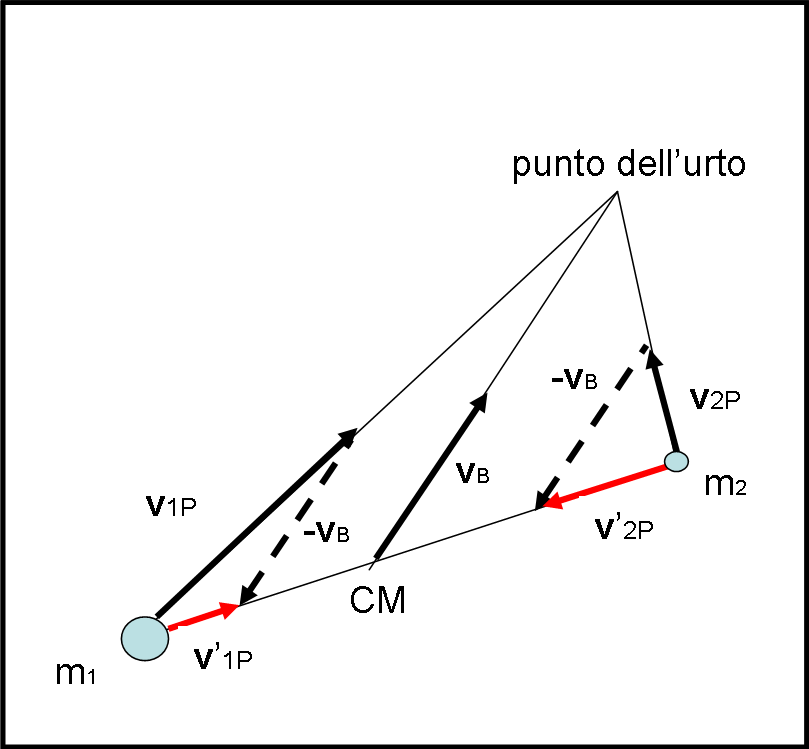
v’_1P e v’_2P sono le velocità delle due particelle prima dell’urto, riferite al sistema del centro di massa, mentre v_1P e v_2P sono quelle del sistema inerziale esterno. La Fig. 1 mostra graficamente la situazione in un urto bidimensionale qualsiasi.

Dimostriamo che la quantità di moto totale prima dell’urto risulta uguale a ZERO.

q’_P= m₁v’_1P + m₂v’_2P = m₁v_1P - m₁v_B + m₂v_2P - m₂v_B = m₁v_1P + m₂v_2P - (m₁ + m₂)v_B

Tuttavia, la velocità del centro di massa può scriversi (ricordando la definizione di centro di massa e derivando):

v_B = (m₁v_1P + m₂v_2P)/(m₁ + m₂)

Sostituendo nella relazione precedente si ottiene:

q’_P = m₁v_1P + m₂v_2P - (m₁ + m₂)v_B = m₁v_1P + m₂v_2P - (m₁ + m₂)(m₁v_1P + m₂v_2P)/(m₁ + m₂)

Semplificando (m₁ + m₂), si ha:

q’_P = m₁v’_1P + m₂v’_2P = m₁v_1P + m₂v_2P - m₁v_1P - m₂v_2P = 0

Analogamente, deve anche essere

q’_D = m₁v’_1D + m₂v’_2D = 0

O, anche:

m₁v’_1P = - m₂v’_2P        …. (1)

m₁v’_1D = - m₂v’_2D       …. (2)

In poche parole, un osservatore piazzato sul centro di massa vede le due masse muoversi verso di lui con quantità di moto uguali e contrarie. La stessa cosa capita dopo l’urto, ma con versi opposti.

Utilizzando queste nuove coordinate si possono ricavare abbastanza facilmente le velocità dopo un urto anelastico. Vedremo che, con e = 1, si ricade nel caso dell’urto elastico che, in un sistema inerziale esterno, avevamo già trattato QUI (effetto Compton) e, con e = 0, nel caso di un urto perfettamente anelastico (vedi dinamica relativistica).

Infine, studieremo il caso in cui la massa di una particella tende a essere infinita e la sua velocità iniziale può essere considerata ZERO.

Urto anelastico

In questo caso non si conserva l’energia cinetica. Le relazioni da considerare sono:

m₁v’_1P = - m₂v’_2P      …. (3)       quantità di moto prima dell’urto

m₁v’_1D = - m₂v’_2D     …. (4)       quantità di moto dopo l’urto

e²(½ m₁v’²_1P + ½ m₂v’²_2P) = ½ m₁v’²_1D + ½ m₂v’²_D2     …. (5)    energia cinetica

Possiamo tranquillamente riferirci a un caso unidimensionale e usare solo i moduli dei vettori.

Le incognite sono, ovviamente, le velocità delle due masse dopo l’urto, v_1D’ e v_2D’.

Dalla (5) si ricava:

m₁(e²v’²_1P - v’²_1D) = m₂(v’²_2D - e²v’²_P2)

ricordando i prodotti notevoli (QUI) si ha:

(a² – b²) = (a – b)(a + b)

E quindi:

m₁(ev’_1P - v’_1D)(ev’_1P + v’_1D) = m₂(v’_2D - ev’_2P)(v’_2D + ev’_2P)    …. (6)

Moltiplichiamo ambo i membri della (3) per e

m₁ev’_1P = - m₂ev’_2P

e le sottraiamo, membro a membro, la (4)

m₁ev’_1P -  m₁v’_1D = - m₂ev’_2P+ m₂v’_2D

m₁(ev’_1P - v’_1D) = m₂(v’_2D -  ev’_2P)      …. (7)

Dividiamo adesso, membro a membro, la (6) e la (7). Possiamo farlo dato che sono due uguaglianze…

ev’_1P + v’_1D = v’_2D + ev’_2P    …. (8)

Le (3) e (4) ci dicono anche che:

m₁v’_1P = - m₂v’_2P

v’_2P = - (m₁/m₂) v’_1P    …. (9)

m₁v’_1D = - m₂v’_2D

v’_2D = - (m₁/m₂) v’_1D   …. (10)

Andiamo a sostituire la (9) e la (10) nella (8)

ev’_1P + v’_1D = - (m₁/m₂) v’_1D - e(m₁/m₂) v’_1P

Siamo riusciti ad avere una relazione con una sola incognita (v’_1D).

Ricaviamola:

v’_1D + (m₁/m₂) v_1D’ = - ev_1P’- e(m₁/m₂) v’_1P

v’_1D (1 + m₁/m₂) = - ev’_1P (1 + m₁/m₂)

v’_1D = - ev’_1P     …. (11)

Attenzione: potremmo anche fermarci qui, pensando al nostro quiz. Tuttavia, siamo ancora nel sistema del centro di massa, mentre noi vogliamo riferirci a Papalla.

Riprendiamo la (8)

 ev’_1P + v’_1D = v’_2D + ev’_2P

e usiamo la (11):

ev’_1P - ev’_1P = v’_2D + ev’_2P

 0 = v’_2D + ev’_2P

E, quindi:

v’_2D = - ev’_2P    …. (12)

Le (11) e (12) risolvono il problema e ci dicono che nel sistema di riferimento del centro di massa le quantità di moto delle due particelle dopo l’urto sono le stesse di quelle prima dell’urto, moltiplicate per e e cambiate di verso:

m₁v’_1D = - m₁ev’_1P      …. (13)

m₂v’_2D = - m₂ev’_2P      …. (14)

le (11) e (12) possono essere riportate al sistema inerziale esterno, ad esempio Papalla, ricordando le relazioni che legano le velocità delle particelle e del centro di massa:

Potete provare a farlo voi e alla fine troverete le due relazioni generali (la soluzione viene data in fondo all’articolo):

v_1D = ((m₁ - em₂)v_1P + (1+ e) m₂v_2P)/(m₁ + m₂)         …. (15)

v_2D = ((1 + e)m₁v_1P + (m₂ - em₁)v_2P)/(m₁ + m₂)         …. (16)

Nel caso in cui e = 1, si ottiene:

v_1D = ((m₁ - m₂)v_1P + 2m₂v_2P)/(m₁ + m₂)

v_2D = ((2m₁v_1P + (m₂ - m₁)v_2P)/(m₁ + m₂)

Proprio le relazioni che avevamo ricavato QUI (formule (5) e (6))

Nel caso in cui e = 0, dobbiamo tener conto che la velocità finale v_D è unica (le due masse si uniscono) ed essa si ricava sia dalla (15) che dalla (16)

v_D = (m₁v_1P + m₂v_2P)/(m₁ + m₂)

In altre parole, la velocità finale è uguale alla velocità del centro di massa prima dell’urto.

Torniamo alla (15) e consideriamo la velocità iniziale della seconda particella (v_2P) uguale a ZERO

v_1D = (m₁ - em₂)v_1P /(m₁ + m₂)

Dividendo numeratore e denominatore per m₂, abbiamo:

v_1D = ((m₁/m₂) - e)v_1P /((m₁/m₂) + 1)         …. (17)

Se la massa m₂ tende a infinito, la (17) si risolve passando al limite:

v_1D = lim _{m2 →∞} ((m₁/m₂) - e)v_1P /((m₁/m₂) + 1) = - ev_1P

Il caso proposto dal nostro quiz può quindi assumere con sufficiente accuratezza che il papallo rimbalzi con una velocità che è praticamente uguale a quella precedente moltiplicata per e (e cambiata di segno).

La faccenda sarebbe leggermente più complicata, dato che la velocità v_2D non può essere ZERO poiché questo fatto comporterebbe la non conservazione della quantità di moto. Essa tende a zero per m₂ che tende a infinito, ma non può essere veramente zero. In realtà, si ha quindi, un leggero allontanamento del riferimento Papalla finale, rispetto al sistema Papalla iniziale. Tuttavia, vale anche la legge di gravità e Papalla viene attirata verso il papallo che ricade, riassumendo la posizione precedente, usata come riferimento fermo, e così via… Insomma, l’approssimazione è più che valida e la possiamo usare tranquillamente.

Soluzione del passaggio da sistema del baricentro a sistema esterno

Abbiamo:

v_1D = v’_1D + v_B

Ma anche:

v’_1D = - ev’_1P

E quindi:

v_1D = - ev’_1P + v_B            …. (18)

Tuttavia, abbiamo anche che:

v_1P = v’_1P + v_B

Ossia:

v’_1P = - (v_B - v_1P)

Sostituendo questo valore nella (18) si ottiene:

v_1D = - ev’_1P + v_B =  - ev_1P + ev_B + v_B = - ev_1P + (1 + e)v_B

Ricordando l’espressione della velocità del centro di massa, si ha:

v_1D = - ev_1P + (1 + e)(m₁v_1P + m₂v_2P)/(m₁ + m₂)

v_1D = (- em₁v_1P - em₂v_1P+ m₁v_1P + em₁v_1P + m₂v_2P + em₂v_2P)/(m₁ + m₂)

v_1D = (- em₂v_1P + m₁v_1P + m₂v_2P + em₂v_2P)/(m₁ + m₂)

v_1D = ((m₁ - em₂)v_1P + (1 + e)m₂v_2P)/(m₁ + m₂)

che è esattamente la (15).

In modo del tutto analogo si ricava la (16) (se proprio non ne avete abbastanza, potete facilmente ricavarla…).

QUI trovate il testo del quiz

QUI trovate la seconda parte della soluzione