Categorie: Meccanica Celeste Sistema Solare
Tags: accelerazione orbitale coordinate polari leggi di Keplero leggi di Newton orbita
Scritto da: Vincenzo Zappalà
Commenti:16
Da Newton a Keplero. 3 ***
Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento
Possiamo continuare nel nostro esercizio riferendo tutto a un piano dato che abbiamo dimostrato che il moto avviene su un piano passante per il Sole. Consideriamo, perciò, la Fig. 1, dove nell’origine vi è il baricentro del Sole S e P rappresenta il baricentro del pianeta che descrive una certa traiettoria da determinare. Siano x e y le coordinate cartesiane di questo punto P.
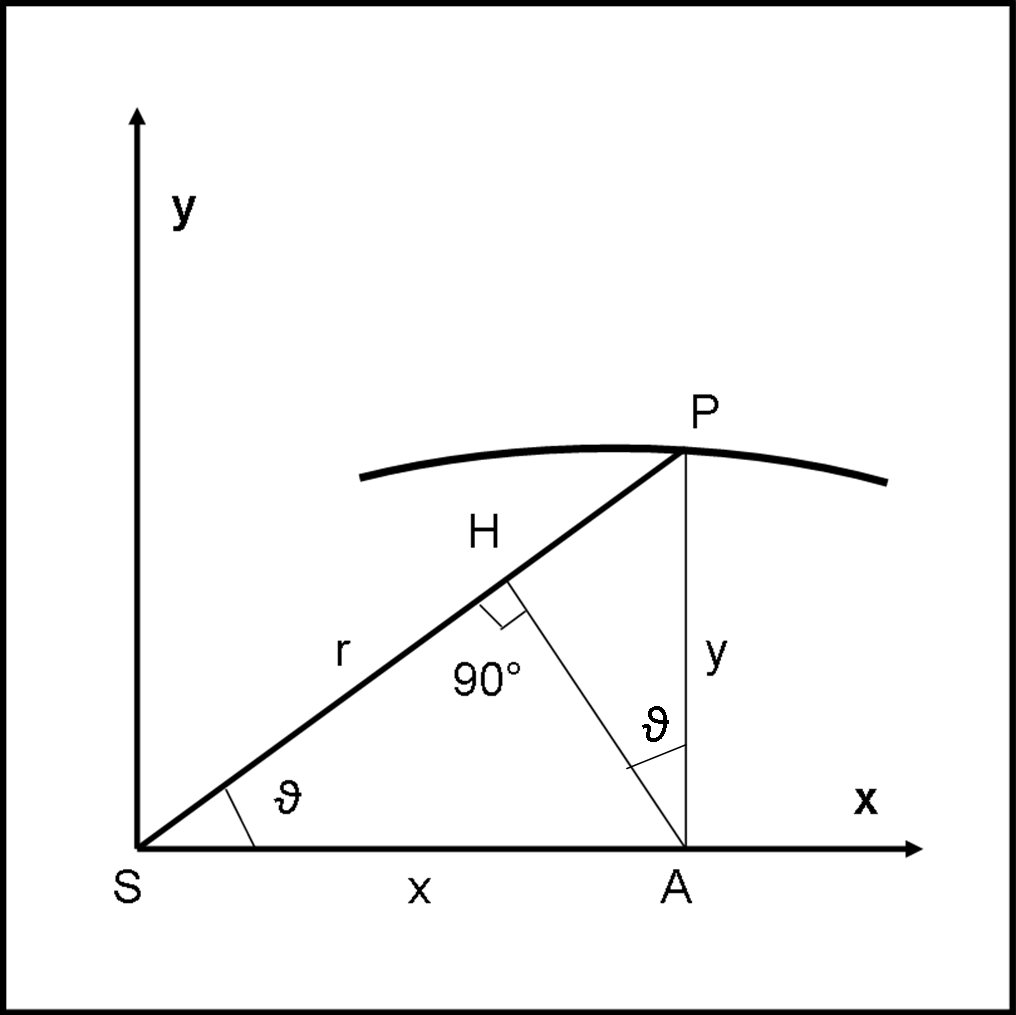
Possiamo immediatamente utilizzare le coordinate polari, dove SP = r:
r cos(ϑ) = x
r sin(ϑ) = y
E, una volta tracciata AH perpendicolare a SP, dai triangoli rettangoli simili SHA e PHA (secondo teorema di Euclide) si ha che l'angolo HAP è uguale a ϑ, da cui:
r = SH + HP = x cos(ϑ) + y sin(ϑ) …. (18)
Le equazioni del moto sono esattamente quelle definite nell’articolo precedente e date dalle (10), in cui consideriamo solo i due assi x e y.
d2x/dt2 + μx/r3 = 0
d2y/dt2 + μy/r3 = 0 …. (19)
Chiamiamo α e β le accelerazioni di P lungo la congiungente SP e lungo la sua perpendicolare.
α è composto dalla somma di due termini che sono le due componenti dell’accelerazione d2x/dt2 e d2y/dt2 lungo la congiungente SP. Deve, allora, essere:
α = d2x/dt2 cos(ϑ) + d2y/dt2 sin(ϑ) …. (20)
Ripetiamo, per non confonderci, non abbiamo fatto altro che calcolare le componenti delle accelerazioni secondo x e y lungo la congiungente SP.
Ricordando le (19) e sostituendo i valori di d2x/dt2 e d2y/dt2, abbiamo anche:
α = d2x/dt2 cos(ϑ) + d2y/dt2 sin(ϑ) = - μx cos(ϑ)/r3 - μy sin(ϑ)/r3 = - μ/r3(x cos(ϑ) + y sin(ϑ))
la parentesi, però, non è altro che la (18) e, quindi:
α = - μr/r3 = - μ/r2
Possiamo scrivere:
α = d2x/dt2 cos(ϑ) + d2y/dt2 sin(ϑ) = - μ/r2 …. (21)
Calcoliamo, adesso β, somma delle componenti delle due derivate secondo la normale a SP.
Se l’angolo tra x e SP è uguale a ϑ, l’angolo tra x e la normale a SP deve essere (90 + ϑ) e quindi le componenti dell’accelerazione secondo la normale saranno date da (vedi QUI):
d2x/dt2 cos(90 + ϑ) = - d2x/dt2 sin(ϑ)
d2y/dt2 sin(90 + ϑ) = d2y/dt2 cos(ϑ)
Per cui β vale:
β = - d2x/dt2 sin(ϑ) + d2y/dt2 cos(ϑ) = μx/r3 sin(ϑ) - μy/r3 cos(ϑ) = (μ/r3)(x sin(ϑ) – y cos(ϑ))
Tuttavia, guardando la Fig. 1 si ha subito che
x sin (ϑ) = AH = y cos(ϑ))
Ossia:
x sin(ϑ) – y cos(ϑ) = 0
E, di conseguenza:
β = - d2x/dt2 sin(ϑ) + d2y/dt2 cos(ϑ) = 0 …. (22)
Non dobbiamo certo stupirci di questo risultato, dato che l’accelerazione è solo radiale…
Non ci resta, adesso, che calcolare i valori di α e β, in coordinate polari, partendo dai valori di x e y. Finora abbiamo preso “per buone” le derivate seconde rispetto al tempo e abbiamo solo visto quanto valgono le componenti lungo SP e lungo la normale a SP.
Partiamo, direttamente, dalle:
x = r cos(ϑ)
y = r sin(ϑ) …. (23)
Dobbiamo stare molto attenti a derivare, dato che sia r che θ sono funzioni del tempo.
Cominciamo con la prima delle (23), derivandola due volte rispetto al tempo:
dx/dt = cos(ϑ) dr/dt - r sin(ϑ) dϑ/dt
d2x/dt2 = - sinϑ (dϑ/dt) (dr/dt) + cosϑ d2r/dt2 - (dr/dt) sinϑ dϑ/dt - r cosϑ(dϑ/dt)2 - r sinϑ dϑ2/dt2
d2x/dt2 = (d2r/dt2) cosϑ - 2 (dr/dt)(dϑ/dt) sinϑ– r (dϑ/dt)2 cosϑ - r (d2ϑ/dt2) sin ϑ …. (24)
Continuiamo con la seconda delle (23):
dy/dt = sinϑ dr/dt + r cosϑdϑ/dt
d2y/dt2 = cosϑ (dϑ/dt) (dr/dt) + sinϑ d2r/dt2 + (dr/dt) cosϑ dθ/dt – r sinϑ (dϑ/dt)2 + r cosϑ dϑ2/dt2
d2y/dt2 = (d2r/dt2) sinϑ+ 2 (dr/dt)(dϑ/dt) cosϑ – r (dϑ/dt)2 sinϑ+ r (dϑ2/dt2) cos ϑ …. (25)
Dopo questa piccola fatica, andiamo a riprendere la (21):
α = d2x/dt2 cos(ϑ) + d2y/dt2 sin(ϑ) = - μ/r2
e inseriamo la (24) e (25)
α = (d2r/dt2) cos2ϑ - 2 (dr/dt)(dϑ/dt) sinϑ cosϑ- r (dϑ/dt)2 cos2ϑ - r (dϑ 2/dt2) sinϑ cos(ϑ) + (d2r/dt2) sin2ϑ + 2 (dr/dt)(dϑ/dt) sinϑ cosϑ - r (dϑ/dt)2 sin2ϑ + r (dθ2/dt2) sinϑ cosϑ
Semplificando:
α = (d2r/dt2) cos2ϑ- r (dθ/dt)2 cos2ϑ + (d2r/dt2) sin2ϑ - r (dϑ/dt)2 sin2ϑ
Raccogliendo:
α = (d2r/dt2)(cos2ϑ + sin2ϑ ) - r (dθ/dt)2 (cos2ϑ + sin2ϑ)
Ricordando che:
(cos2ϑ + sin2ϑ) = 1
Abbiamo, infine:
α = (d2r/dt2) - r (dϑ/dt)2 = - μ/r2 …. (26)
Analogamente, possiamo prendere la (22) e inserire al suo interno le (24) e (25)
β = - d2x/dt2 sin(ϑ) + d2y/dt2 cos(ϑ) = 0
β = - (d2r/dt2) sinϑ cosϑ + 2 (dr/dt)(dϑ/dt)sin2ϑ + r (dϑ/dt)2 sinϑ cosϑ+ r (dϑ2/dt2)sin2ϑ
+ (d2r/dt2)sinϑ cosϑ + 2 (dr/dt)(dϑ/dt) cos2ϑ – r (dϑ/dt)2 sinϑ cosϑ + r (dϑ2/dt2) cos2ϑ
E, infine:
β = + 2(dr/dt)(dϑ/dt) + r (dϑ2/dt2) = 0 …. (27)
Moltiplichiamo e dividiamo quest’ultima equazione per r:
(1/r) (2r(dr/dt)(dϑ/dt) + r2(dϑ2/dt2)) = 0 …. (28)
Ciò che moltiplica 1/r non è altro che la derivata rispetto al tempo di r2(dϑ/dt). Proviamolo…
d(r2(dϑ/dt))/dt = 2r (dr/dt) (dϑ/dt) + r2(dϑ2/dt2)
Ma, allora, la (28) può essere scritta:
(1/r) d(r2(dϑ/dt))/dt = 0
Per r diverso da infinito (altrimenti l’equazione darebbe zero qualsiasi sia il valore della derivata), si ha:
r2(dϑ/dt) = costante = h …. (29)
Provate ad analizzarla da soli e a vedere cosa significa sia analiticamente che fisicamente…






16 commenti
scusate la Figura in evidenza tagliata, ma non si riesce a risolvere il problema... Ancora un po' di pazienza. nell'articolo è completa!
è la lunghezza dell'arco infinitesimo di una circonferenza di raggio r sotteso dall'angolo
per cui il prodotto ne è il doppio dell'area del settore compreso sotto detto arco
trattandosi di un punto mobile su un arco la grandezza è un area coperta in un certo intervallo di tempo che in questo caso è costante come enunciato con la seconda legge di Kepler
e che cosa vuol dire anche? pensa alla quantità di moto...
vediamo
è la velocità istantanea, che a meno della massa, è la quantità di moto del corpo
la direzione è tangenziale all'arco di traiettoria infinitesimo considerato
il prodotto per il raggio è quindi il momento della quantità di moto per una massa unitaria che è costante
come deve essere, se ho capito, dato che l'accelerazione è esclusivamente radiale (22)
è la velocità istantanea
...
non vedo le formule inserite con il tasto fx
Caro Gianni,
tutti i problemi sul nuovo blog sarebbe bene metterli nei commenti relativi a "cambiamo vestito"
caro Gianni,
perfetto! E, quindi, se il momento angolare è costante (che è la seconda legge di Keplero, in fondo), vuol dire che il vettore è sempre lo stesso e di conseguenza e l'orbita deve essere complanare! Con un prodotto vettoriale immediato (con forza radiale) si dimostrava subito che l'orbita sta su un piano. Noi ci siamo divertiti con un po' di geometria analitica... anche perché ci servirà dopo
Caro Enzo, come vedi ho finalmente ripreso la lettura degli articoli su Keplero.
In particolare per capire questo articolo sono andato a ripassare gli articoli sul Momento angolare.
Inoltre, per provare a capire meglio alcuni problemi geometrici ho realizzato delle figure, che spero non contengano errori..
La prima mi è servita per capire perché i due angoli in A e in S sono uguali.
La seconda semplicemente per evidenziare il segmento r (SP) e per ragionare sull'accelerazione
α (radiale) e sulle due componenti x e y.
L'ultima per ragionare sull'accelerazione β... ricordano le funzioni oscillanti...
Infine, quello che mi sembra di notare nella formula: r²(dϑ/dt) = costante = h….
è che se considero che dϑ/dt è una velocità angolare e che se considero che l'inerzia di un corpo in rotazione è uguale a I= m r², ciò che sembra suggerire la formula è che il momento angolare non cambia, è costante: L = I ω = m r²(dϑ/dt)
D'altronde la Forza in gioco è di natura centripeta, ossia lungo r, per cui il suo Momento è nullo e il Momento angolare rimane costante (se aumenta r dovrà ridursi ω e viceversa... ).
Paolo
grande Paolo... come sempre. Non c'è più gusto a chiedere le cose... c'è un gruppetto di spietati esperti (prima o poi andrò in crisi io...)
Figure molto chiare, come sempre, Paolo. Con riferimento alla prima, guardandola mi è venuto in testa un modo alternativo, forse più immediato, per dimostrare che alfa è uguale a teta. Considerando il triangolo rettangolo HSA, si ha subito che l'angolo HAS è uguale a 90-teta (somma angoli interni di un triangolo = 180). Se ora considero l'angolo retto PAS, deve essere (90-teta)+alfa=90. Da cui alfa=teta.
Direi che il metodo alternativo che hai indicato non fa una grinza
Paolo
sempre agguerriti i miei collaboratori Comunque, due angoli formati da rette perpendicolari sono uguali...
Comunque, due angoli formati da rette perpendicolari sono uguali...
BA è perp. a SA e AH è perp. a SP...
PA non BA... dov'é la B nella figura?

eh no! Io parlo della prima figura di Paolo, dove compare alpha... questa volta ho ragione io

Ebbene sì... per questa volta sì! Io avevo guardato l'ultima
Pfuiiii.... per questa volta è andata....