Questo lungo articolo riunisce tutti quelli relativi alla geometria sferica. Esso è stato anche inserito tra gli approfondimenti.


Questo lungo articolo riunisce tutti quelli relativi alla geometria sferica. Esso è stato anche inserito tra gli approfondimenti.
Questa puntata è estremamente corta e anche molto facile. Anche la terza formula fondamentale si ottiene partendo dalla prima e giocando un po’ con la matematica (roba da poco).
La seconda formula fondamentale è sicuramente la più “difficile” da ottenere. Non spaventatevi, però… sono solo passaggi matematici alla portata di tutti. Inoltre, si può notare come piccoli “trucchi” possano rendere la matematica estremamente intrigante e utilissima per mettere alla prova la nostra capacità di seguire ragionamenti logici di importanza ben più generale.
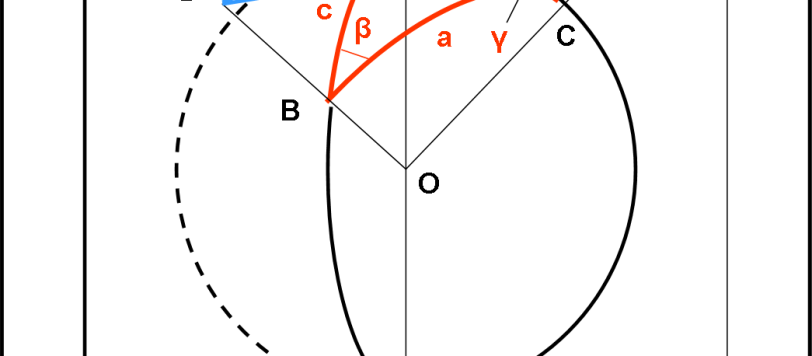
Definito il triangolo sferico, sia intrinsecamente che estrinsecamente, non ci resta che determinare alcune formule fondamentali che leghino tra loro i lati e gli angoli. Esse vengono proprio chiamate le tre formule fondamentali della trigonometria sferica.
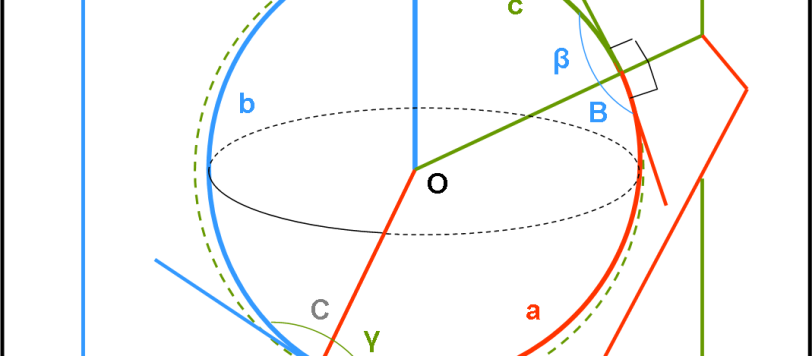
Vorremmo continuare con la descrizione della trigonometria sferica, per potere poi maneggiare senza problemi la sfera celeste e le posizioni dei corpi che sono proiettati su di lei. Tuttavia, è prima necessario introdurre dei teoremi di trigonometria piana che avevamo tralasciato descrivendone le basi. Prima ancora, però, diamo le soluzioni ai due quiz proposti la volta scorsa.
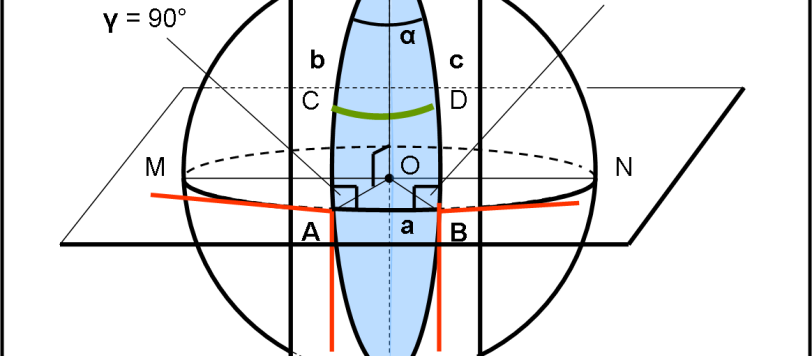
Definiti i lati di un triangolo sferico, non ci resta che definire quali siano i suoi angoli. Nel fare questo, risolviamo il vecchio quiz e stabiliamo anche un’altra proprietà molto interessante dei triangoli sferici. Concludiamo con due nuovi quiz, che saranno risolti la volta successiva.

Tutto diventa più semplice utilizzando una visione estrinseca. Tuttavia, aver lavorato solo su uno spazio a due dimensioni non euclideo (a parte le figure) ci ha sicuramente fatto entrare meglio nella problematica. Trovate molte ripetizioni, ma non picchiatemi... Certi concetti vanno digeriti molto bene!
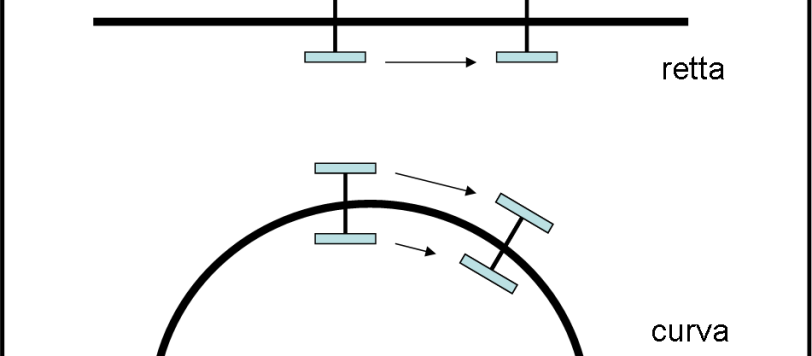
Iniziamo la nostra vita su una superficie sferica, obbligandoci a ragionare e a definire la geometria su di essa senza sfruttare la nostra capacità di osservare nelle tre dimensioni. Un impegno non sempre immediato, ma che deve essere affrontato per capire perfettamente una geometria non euclidea, la geometria che governa la sfera celeste (e anche la superficie terrestre), ma non solo. Ripeteremo, poi, gli stessi concetti usando una visione estrinseca, decisamente più comoda, ma i due metodi usati per giungere alla stessa meta daranno un quadro veramente completo della situazione

Questo articolo vuole essere l’introduzione alla geometria sferica, che ci permetterà di descrivere il cielo stellato e le coordinate celesti. Tuttavia, è anche il primo passo verso uno spazio e addirittura uno spaziotempo curvo, base fondamentale per affrontare la Relatività Generale. Non perdetevi, perciò, le varie puntate…

La storia scritta nei libri è, spesso, come un telefono senza fili. L’inizio è sicuramente giusto, ma poi, di passaggio in passaggio, prende un risvolto molto diverso e ben lontano dall’originale. Prendiamo, per esempio, la scoperta dell'America... un passo fondamentale per l'uomo di cui Cristoforo Colombo è considerato l'epico eroe. Ma sarà davvero così?
Se mando un segnale su Venere, posizionato dalla parte opposta del Sole rispetto alla Terra, e aspetto che torni indietro, mi accorgerò che il tempo impiegato è maggiore di quello calcolato teoricamente. Come mai? Basta tener presente che la luce è dovuta transitare due volte nei pressi del Sole... Ciò vuol forse dire che la velocità della luce è diminuita? Chiedetelo a Shapiro.

Ci uniamo alle celebrazioni del settecentenario della morte di Dante Alighieri, riproponendo un progetto di cui andiamo molto fieri, nel quale letteratura, storia e scienza si intrecciano lungo un intervallo di tempo che va dal medioevo più cupo alla cosmologia più moderna: un entusiasmante viaggio al termine del quale dimostreremo, tramite l'analisi dei suoi stessi versi, la capacità del Sommo Poeta di immaginare una struttura teologica e scientifica ben al di là dei suoi tempi, anticipando di fatto la visione matematica di Riemann e quella fisica di Einstein.

Ci uniamo alle celebrazioni del settecentenario della morte di Dante Alighieri, riproponendo un progetto di cui andiamo molto fieri, nel quale letteratura, storia e scienza si intrecciano lungo un intervallo di tempo che va dal medioevo più cupo alla cosmologia più moderna: un entusiasmante viaggio al termine del quale dimostreremo, tramite l'analisi dei suoi stessi versi, la capacità del Sommo Poeta di immaginare una struttura teologica e scientifica ben al di là dei suoi tempi, anticipando di fatto la visione matematica di Riemann e quella fisica di Einstein.

In questo articolo descrivo la realizzazione di un modello di geometria solida con il quale ho voluto verificare il funzionamento di una montatura equatoriale, ossia un particolare sostegno di un telescopio molto utilizzato in ambito amatoriale e non solo. La montatura equatoriale consente con un unico movimento, manuale o motorizzato, di "inseguire" il moto apparente di un astro nel cielo, in realtà ruotando in sincrono col moto di rotazione terrestre.

Ci uniamo alle celebrazioni del settecentenario della morte di Dante Alighieri, riproponendo un progetto di cui andiamo molto fieri, nel quale letteratura, storia e scienza si intrecciano lungo un intervallo di tempo che va dal medioevo più cupo alla cosmologia più moderna: un entusiasmante viaggio al termine del quale dimostreremo, tramite l'analisi dei suoi stessi versi, la capacità del Sommo Poeta di immaginare una struttura teologica e scientifica ben al di là dei suoi tempi, anticipando di fatto la visione matematica di Riemann e quella fisica di Einstein.