Si è cercato da newton a keplero | L'Infinito Teatro del Cosmo

01/07/16

Il problema dei due corpi: da Newton a Keplero ***

Categorie: Matematica, Meccanica Celeste, Senza categoria Tags: legge di gravitazione universale, orbite planetarie, tre leggi di Keplero. Leggi della dinamica Scritto da: Vincenzo Zappalà Commenti:3

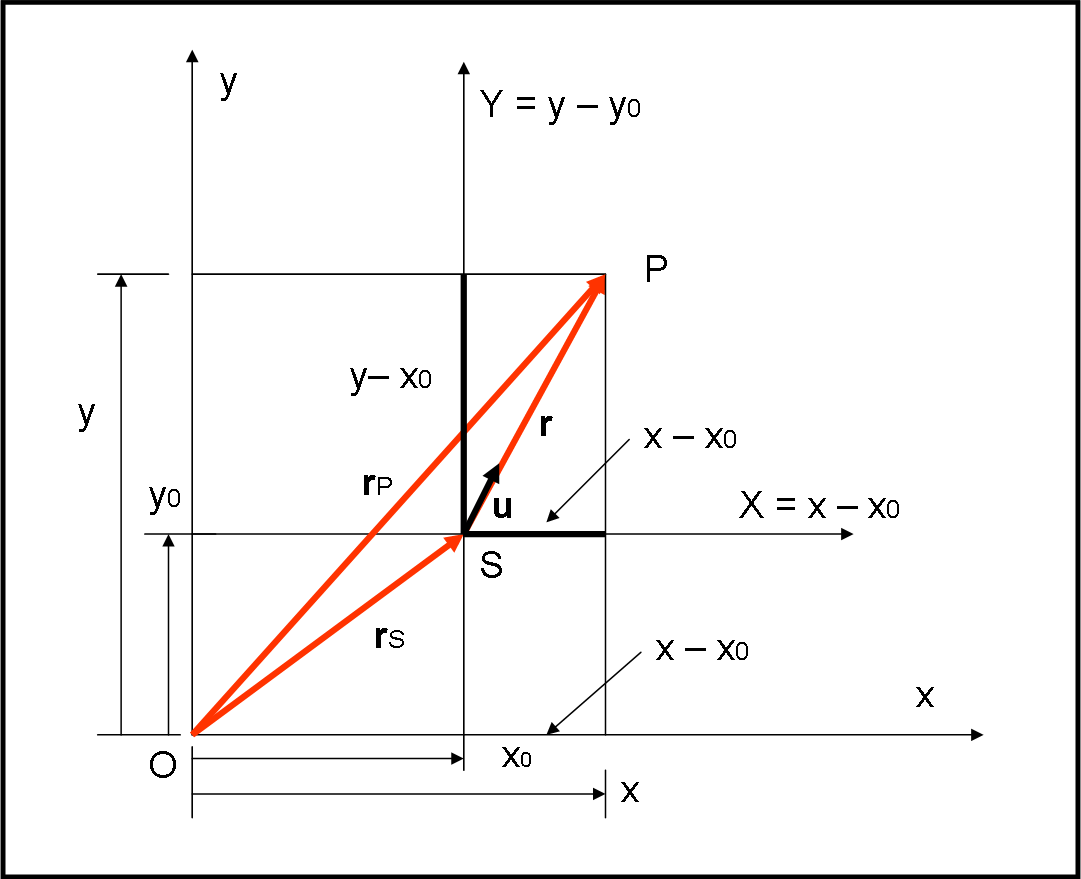
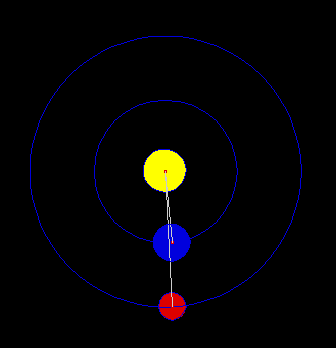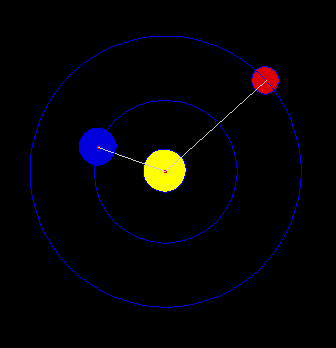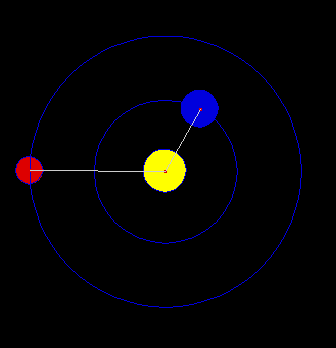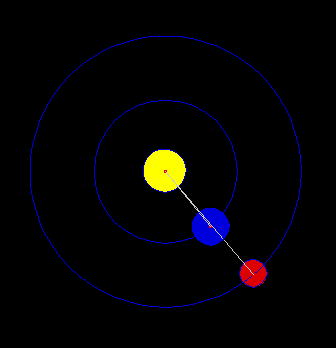
Attraverso tanti calcoli analitici (di media difficoltà, anche se un po' noiosi) si possono ricavare le tre leggi di Keplero partendo dalla legge di gravitazione universale di Newton. Vi è un solo punto critico relativo alla derivazione della traiettoria del corpo orbitante: un'equazione differenziale che comporta il calcolo di un integrale non banale (per noi almeno). Solo in questo caso accettiamo di prendere un risultato per buono... Per dirla in altre parole, risolviamo un problema fondamentale di Meccanica Celeste: il problema dei due corpi.

09/06/16

Da Newton a Keplero. 6 ***

Categorie: Meccanica Celeste Tags: forza centrifuga, forza di gravità, Newton, periodo, semiasse, terza legge Keplero, velocità areolare Scritto da: Vincenzo Zappalà Commenti:0

Non ci resta che dedurre la terza legge di Keplero, quella forse più importante e usata. La deduciamo per un’orbita qualsiasi, ma è già ben noto (e immediato) il procedimento da usare nel caso di un’orbita circolare, che richiamiamo per semplicità.

30/05/16

Da Newton a Keplero. 5 ***

Categorie: Meccanica Celeste Tags: equazione differenziale, forza centrale, Keplero, Newton, orbita ellittica Scritto da: Vincenzo Zappalà Commenti:1

Bando alle ciance e andiamo dritti fino alla prima legge di Keplero, la parte più difficile, che ci obbliga a prendere per buona la soluzione di un’equazione differenziale. Per noi è, al momento, troppo impegnativa, ma chi vuole saperne di più trova un link adeguato.

23/05/16

Da Newton a Keplero. 4 ***

Categorie: Meccanica Celeste Tags: forza centrale, momento angolare, seconda legge di Keplero Scritto da: Vincenzo Zappalà Commenti:2

Quasi senza accorgercene abbiamo ricavato la seconda legge di Keplero. Soffermiamoci un poco su di lei e sul suo significato fisico. Poi proseguiremo verso la prima legge.

15/05/16

Da Newton a Keplero. 3 ***

Categorie: Meccanica Celeste, Sistema Solare Tags: accelerazione orbitale, coordinate polari, leggi di Keplero, leggi di Newton, orbita Scritto da: Vincenzo Zappalà Commenti:16

Affrontiamo in modo analitico la prima legge di Keplero. Ci accorgeremo che per arrivarci dobbiamo passare attraverso la seconda che acquista non solo un significato fisico ben preciso, ma che ci dimostra che il fatto che l’orbita giace su un piano poteva ricavarsi in modo immediato. C'è tanta matematica, quindi forza e coraggio... ma ne vale la pena!

06/05/16

Da Newton a Keplero. 2 ***

Categorie: Fisica classica, Meccanica Celeste Tags: ellisse, ellissi, legge di gravitazione universale, leggi di Keplero, leggi di Newton, orbite planetarie, piano orbitale, versori, vettori Scritto da: Vincenzo Zappalà Commenti:6

Dedichiamoci al problema più “difficile”, ossia a quello di ricavare il moto ellittico partendo dalla leggi di Newton. Ci accorgeremo che prima di arrivare alla fine, incontreremo già la seconda legge di Keplero, oltre che fare amicizia con un piano. In questa prima parte ci fermeremo proprio su questo piano. Procediamo con molta lentezza e chiarezza. Alla fine il moto orbitale avrà ben pochi segreti...

01/05/16

Da Newton a Keplero. 1 **

Categorie: Fisica classica, Meccanica Celeste Tags: coordinate polari, ellisse, ellissi, equazioni differenziali, integrali definiti, legge di gravitazione universale, leggi di Keplero, Newton Scritto da: Vincenzo Zappalà Commenti:7

Iniziamo un discorso estremamente importante: partendo dalla legge di Newton vogliamo arrivare alle leggi di Keplero. Può sembrare strano, ma è un argomento trattato raramente, anche se è veramente fondamentale, riferendosi al moto di due corpi. In questo primo articolo ricordiamo le coordinate polari, descriviamo un’ellisse e introduciamo un nuovo tipo di equazione, in modo estremamente semplificato.

18/10/19

Keplero e Newton rivisitati da Feynman. 5 : la curva è proprio un'ellisse! **

Categorie: Meccanica Celeste Tags: costruzione ellisse, diagramma velocità, Feynman, percorso della luce, riflessione, traiettoria dei pianeti Scritto da: Vincenzo Zappalà Commenti:0

Nella puntata precedente eravamo riusciti a costruire il diagramma delle velocità basandoci sui primi due principi della dinamica e sulle prime due leggi di Keplero. Non ci resta che utilizzare questo geniale diagramma per dimostrare che la curva della traiettoria è proprio un'ellisse. Chi ha seguito i vari articoli si sarà già accorto che il diagramma delle velocità assomiglia in tutto e per tutto al cerchio iniziale della prima puntata. Basterebbe applicare a lui il procedimento usato allora e salterebbe fuori l'ellisse.

10/10/19

Keplero e Newton rivisitati da Feynman. 4 : Il diagramma delle velocità **

Categorie: Meccanica Celeste Tags: diagramma velocità, Feynman, forza di gravità, le orbite dei pianeti, tre leggi di Keplero Scritto da: Vincenzo Zappalà Commenti:1

Abbiamo costruito il diagramma delle velocità corrispondente a una traiettoria che segua la seconda legge di Keplero e in cui la forza di attrazione vada con l'inverso della distanza al quadrato. Tuttavia, non sappiamo ancora che traiettoria sia e, soprattutto, non abbiamo ancora dimostrato che il diagramma delle velocità sia proprio un poligono regolare. Iniziamo con quest'ultimo problema.

04/10/19

Keplero e Newton rivisitati da Feynman. 3 : La forza di gravità **

Categorie: Meccanica Celeste Tags: diagramma orbitale, diagramma velocità, Feynman, Keplero, moto pianeti attorno al Sole, Newton Scritto da: Vincenzo Zappalà Commenti:0

La volta scorsa eravamo rimasti "in panne" dato che, pur avendo ricavato la seconda legge di Keplero, ben poco si poteva dire sulla traiettoria di un pianeta attorno al Sole. Per fare questo passo in avanti è necessario conoscere come agisce la forza esercitata dal Sole, in funzione della distanza del pianeta. Ho aggiunto un asterisco solo perché bisogna capire molto bene la costruzione elementare di un nuovo diagramma...

30/09/19

Keplero e Newton rivisitati da Feynman. 2 : La seconda legge di Keplero *

Categorie: Meccanica Celeste Tags: area spazzata, Feynman, Keplero, momento angolare, moto dei pianeti, Newton, primo principio dinamica, secondo principio dinamica Scritto da: Vincenzo Zappalà Commenti:0

Non stupitevi dell'unico asterisco inserito nel titolo. L'articolo, in realtà, non va oltre e ciò che è necessario sapere per poterlo seguire senza problemi sono i primi due principi della dinamica di Newton e il calcolo dell'area di un triangolo qualsiasi. I concetti sono quelli usati da Feynman anche se ho cercato di renderli ancora più ... elementari, attraverso molte figure ed esempi.

25/09/19

Keplero e Newton rivisitati da Feynman. 1 : La costruzione dell’ellisse *

Categorie: Meccanica Celeste Tags: ellisse, ellissi, Feynman, Keplero, lezione, moto dei pianeti, Newton Scritto da: Vincenzo Zappalà Commenti:2

Il quiz sulla costruzione dell’ellisse era solo un antipasto per una ghiotta e geniale lezione di Richard Feynman. Da Newton a Keplero senza equazioni differenziali e con una matematica e geometria alla portata di tutti coloro che vogliono usare la propria intelligenza e divertirsi, ammirando uno dei più grandi geni al lavoro.

04/06/21

La storia dell'Unità Astronomica (3): Keplero e le sue leggi

Categorie: Sistema Solare, Storia della Scienza Tags: astrometria, Horrocks, Huygens, Keplero, transito di Venere, Unità Astronomica Scritto da: Vincenzo e Daniela Commenti:0

Dopo secoli di disinteresse per il calcolo della distanza Terra-Sole (e quindi delle reali dimensioni del Sistema Solare), Keplero mostra quanto questa misura sia una chiave straordinaria per aprire la porta dell’Universo, quello vero. Le sue tre leggi dicono molte cose: in particolare, offrono la possibilità di calcolare le orbite dei pianeti. Ma manca ancora il fattore scala…

01/06/20

Rivalutiamo Keplero *

Categorie: Astronomia Elementare, Cosmologia, Meccanica Celeste, Storia della Scienza Tags: dodecaedro, Keplero, Pitagora, poliedri regolari, solidi platonici, teoria eliocentrica, Tetraktis, tre leggi di Keplero Scritto da: Vincenzo Zappalà Commenti:0

A volte si pensa: "Ma come ha fatto Keplero a enunciare tre leggi praticamente perfette pensando e tracciando poliedri e sfere che li racchiudevano?". In realtà il modello kepleriano del Sistema Solare sembra più un gioco di incastri, cosparso di un forte sapore esoterico. Non per niente, la base di tutto è la visione filosofica di Platone e quella mistica e geometrica di Pitagora. Ma proprio questa simbologia, apparentemente risibile per occhi moderni, ha fatto scattare varie molle di puro intuito scientifico, provocando una rivoluzione epocale, quasi paragonabile a quella einsteniana.

19/09/19

Costruiamo un'ellisse e imiteremo Newton ***

Categorie: Matematica, Meccanica Celeste Tags: cerchio, costruzione, ellisse, ellissi, quiz Scritto da: Vincenzo Zappalà Commenti:10

Ci sono molti modi per costruire graficamente un'ellisse, ma tra i tanti proviamo a trovarne uno che ci permetterà di imitare Newton senza alcuna equazione differenziale. Un quiz che è solo l'ingresso in un mondo straordinario. Chi conosce la storia è pregato di tacere e fare pensare tutti gli altri... grazie!

07/12/16

Gli elementi orbitali e le "anomalie" di Keplero ***

Categorie: Meccanica Celeste Tags: anomalia eccentrica, anomalia media, anomalia vera, elementi orbitali, equazione del centro, equazione di Keplero Scritto da: Vincenzo Zappalà Commenti:0

In questo articolo, torniamo alle leggi di Keplero per definire ancora meglio le loro enormi potenzialità, specialmente se legate alla legge di Newton. Vi assicuro che sono argomenti tutt’altro che noiosi e -forse- non troppo conosciuti.

155 Search Results for "da newton a keplero"