In questo articolo della serie dedicata alle superfici di rotazione ricaviamo la rappresentazione analitica di iperboloidi di rotazione a una falda e a due falde. Possibilità di visualizzare i relativi modelli geometrici, anche in 3D.
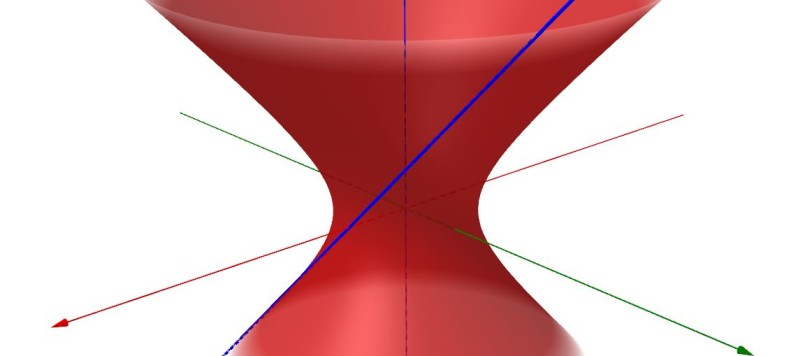

In questo articolo della serie dedicata alle superfici di rotazione ricaviamo la rappresentazione analitica di iperboloidi di rotazione a una falda e a due falde. Possibilità di visualizzare i relativi modelli geometrici, anche in 3D.
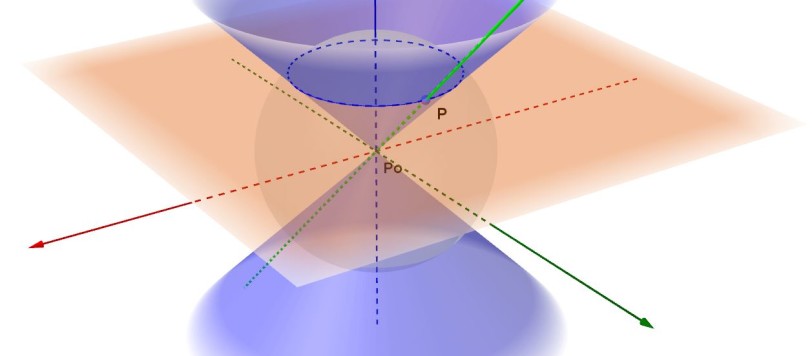
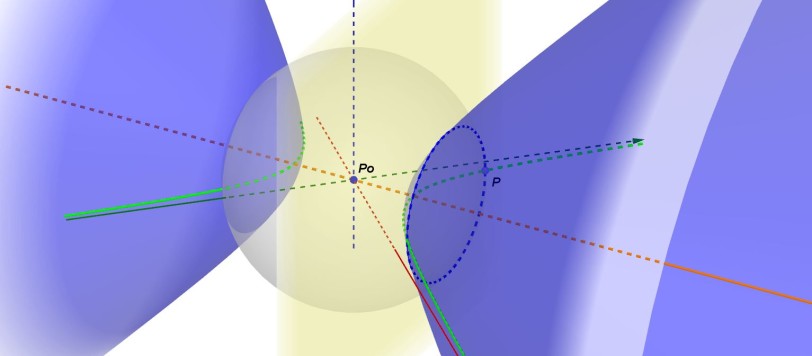
Nel mio precedente articolo ho cercato di spiegare cosa siano in geometria dello spazio le superfici di rotazione e un metodo per determinarne la rappresentazione analitica. In questo articolo fornirò una prima serie di esempi, più semplici, utilizzando ancora la possibilità di visualizzazione tridimensionale anche attraverso l'uso di occhiali anaglifici. Rammento per comodità che una […]
In questo articolo faremo la conoscenza di una particolare entità geometrica spaziale che ritroviamo in molti esempi della realtà che ci circonda: la superficie di rotazione. Vedremo, inoltre, come ricavarne la rappresentazione analitica. Come si intuisce dal suo stesso nome, tale entità geometrica è generata dalla rotazione di una curva attorno ad una retta, detta […]
In questa pagina sono raccolti gli articoli sulla geometria dello spazio scritti da Arturo Lorenzo Introduzione alla geometria dello spazio - 1° parte Introduzione alla geometria dello spazio - appendice Introduzione alla geometria dello spazio - 2° parte Geometria dello spazio - 3° parte Geometria dello spazio - 4° parte Geometria dello spazio - 5° […]
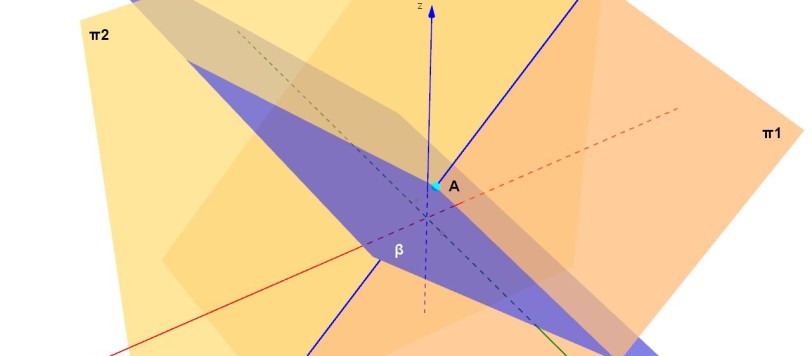
Nel precedente articolo, che potete rileggere QUI, ho introdotto il concetto di parametri direttori di una retta nel piano. In questo estendiamo il concetto alla retta nello spazio e al piano. Passiamo, quindi, nel riferimento cartesiano dello spazio.
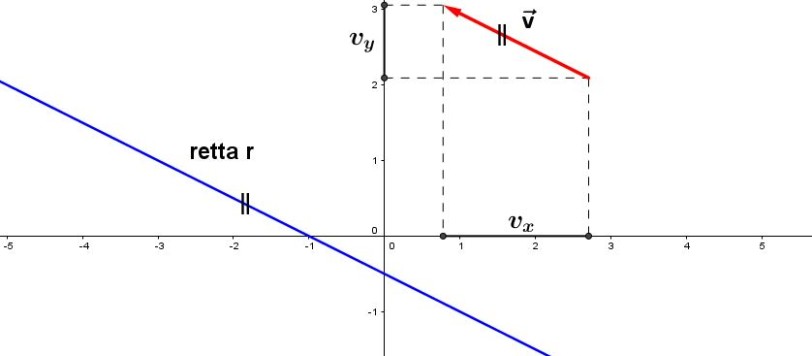
In questo articolo e in quello successivo intendo illustrare un elemento sinora da me mai citato ma che , come vedremo, si rivela molto utile nella trattazione di problemi di geometria, in particolare quella dello spazio. Tale elemento caratterizza una retta, indicandone la direzione, oppure un piano, consentendoci di individuarne subito tutte le infinite rette ad esso perpendicolari. Scopriremo che sia la retta sia il piano si "portano dietro" questo elemento come una targa identificativa, che a noi basta quasi leggere per conoscere subito, in termini analitici, la direzione della retta o la giacitura del piano.
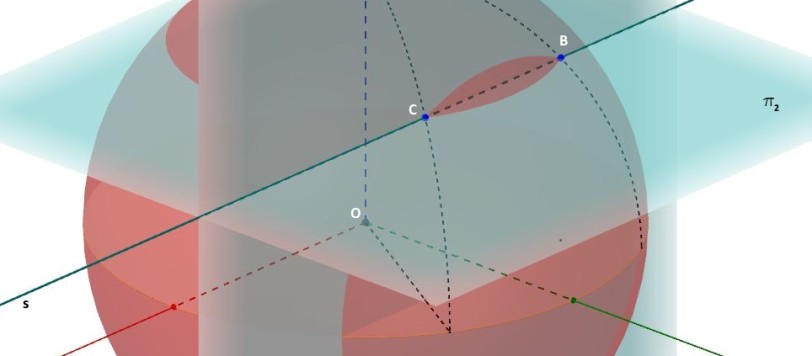
Dopo il primo articolo sulla geometria solida, pubblicato in due parti QUI e QUI nelle scorse settimane, eccoci ora giunti a questa appendice. In essa, mettendo in pratica i concetti di geometria solida sinora esposti, con particolare riferimento al piano, al fascio proprio di piani e alla sfera, dimostreremo che, dati due punti su una […]

Proseguiamo il nostro percorso nella geometria dello spazio con la seconda parte dell'articolo. La numerazione delle figure e delle formule segue quella della prima parte dell'articolo, che trovate QUI. Fasci di rette nel piano e fasci di piani nello spazio Nel piano le rette posso essere tra loro incidenti, quando hanno un punto in […]
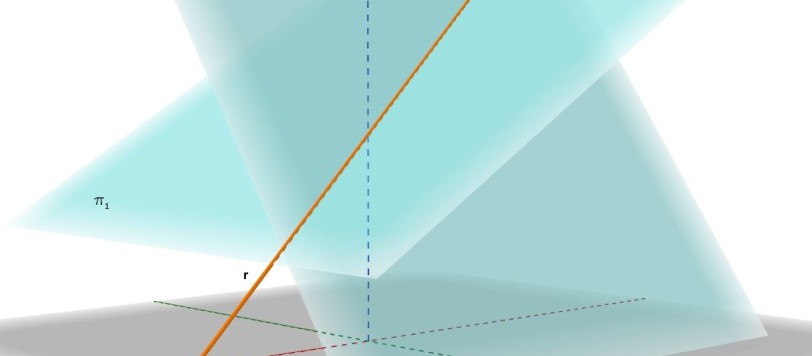
Obiettivo di questo articolo, di cui viene pubblicata ora la prima parte, è quello di entrare nell'affascinante mondo della geometria dello spazio e, dopo la seconda parte, dimostrare che la curva congiungente due punti situati su una superficie sferica e che misuri la minore distanza tra essi è un arco di circonferenza massima, ossia avente centro coincidente con quello della sfera.

Riporto le soluzioni in un articolo a parte vista la lunghezza non indifferente... L'approccio cinematico è molto simile a quello di Fabrizio. Inoltre, trovate anche la soluzione analitica (riassunta nel commento di Fabrizio) che rappresenta di per sé un approccio più laborioso, ma altrettanto istruttivo.

Questo articolo mi ha fatto faticare non poco. Spero che, anche se in parte molto personale, possa aiutare a comprendere e a riflettere. Ho messo tre asterischi, anche se avrei desiderato ardentemente di metterne uno solo. Spero di cuore, però, che la vostra reazione lo faccia calare di grado... se non proprio un asterisco, magari due...

In questo articolo descrivo la realizzazione di un modello di geometria solida con il quale ho voluto verificare il funzionamento di una montatura equatoriale, ossia un particolare sostegno di un telescopio molto utilizzato in ambito amatoriale e non solo. La montatura equatoriale consente con un unico movimento, manuale o motorizzato, di "inseguire" il moto apparente di un astro nel cielo, in realtà ruotando in sincrono col moto di rotazione terrestre.

Ebbene sì, voglio provarci, semplificando il tutto e attribuendogli solo un asterisco. I più esperti non mi guardino male, dato che bisogna pure incominciare...

E' bello scoprire anche aspetti artistici e geometrici in ciò che avviene nell'Universo. Nei giorni scorsi, desideroso di avere un mio modello geometrico da cui ricavare in qualsiasi momento la distanza tra Venere e la Terra, ho implementato nel solito software Geogebra le orbite dei due pianeti. Ecco a voi il risultato!

La tradizione vuole che si debba arrivare a comprendere il presente ripercorrendo la storia passata. Ma la discontinuità tra il modello Newtoniano, estremamente intuitivo e tangibile, e quello Einsteiniano, più generale e più lontano dalle esperienze quotidiane, è tanto più insormontabile, quanto più prolungata è la familiarità con il pensiero tradizionale.
Invece di trasmettere "certezze" superate da oltre un secolo, è necessario creare una mentalità orientata già da subito ad accogliere la corretta e più ampia visione della realtà, negli anni in cui le menti sono più ricettive ed elastiche, immuni da polarizzazioni e tabù. Forse avremo anche una società più attenta e smaliziata.
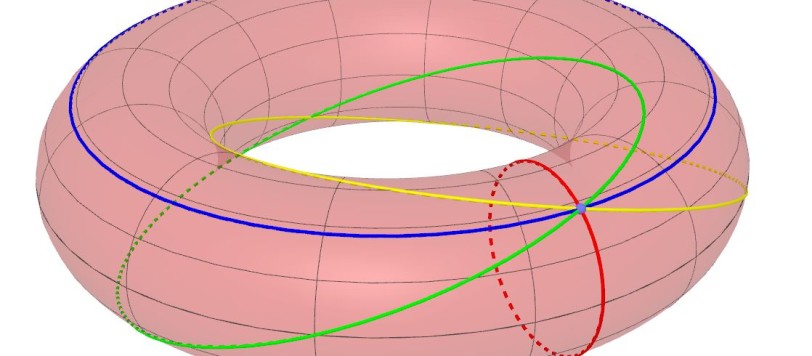
In questa appendice all'articolo sul toro analizzeremo le curve risultanti dalla sezione del toro con determinati piani secanti. Scopriremo le bellissime circonferenze di Villarceau, l'ippopede di Proclo , gli ovali di Cassini, le lemniscate di Booth e di Bernoulli. Vedremo come la geometria solida sa regalarci momenti di autentica meraviglia. L'appendice è divisa in due parti. La prima è dedicata alle sole circonferenze di Villarceu.