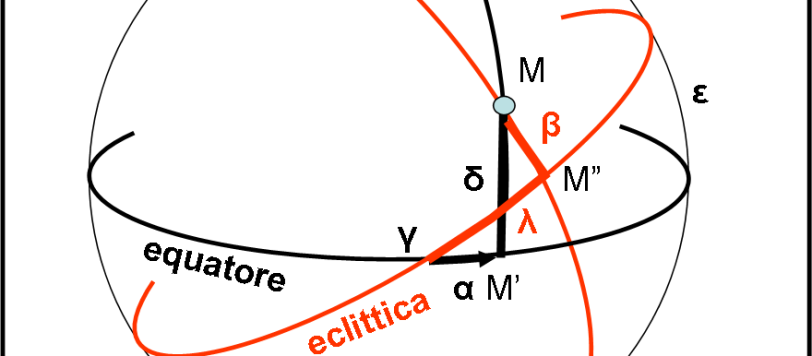
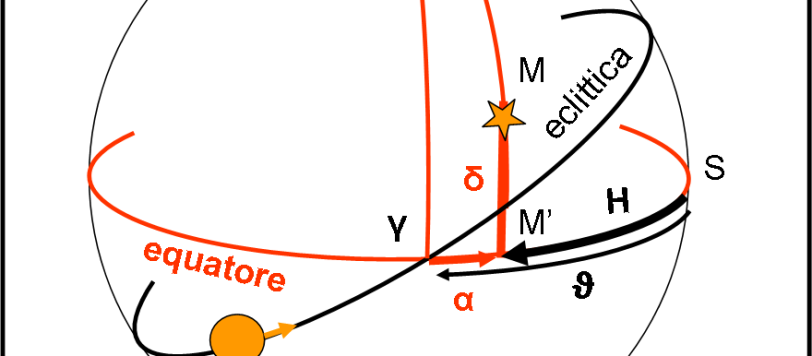
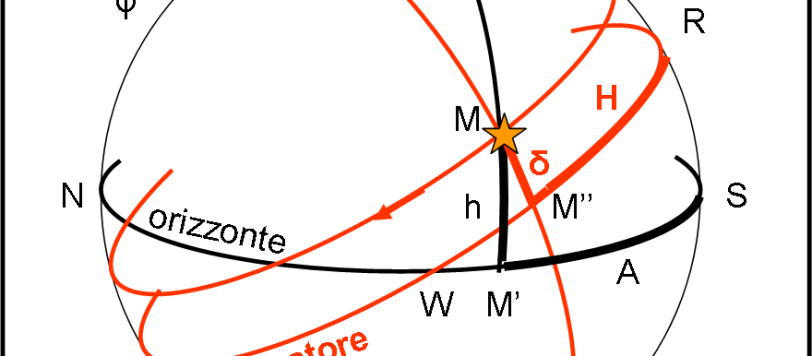
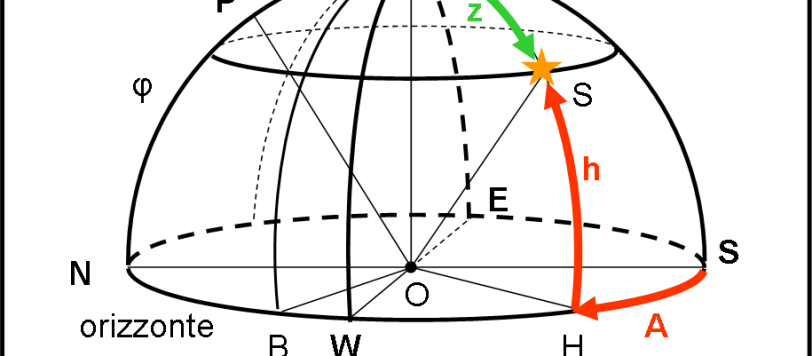
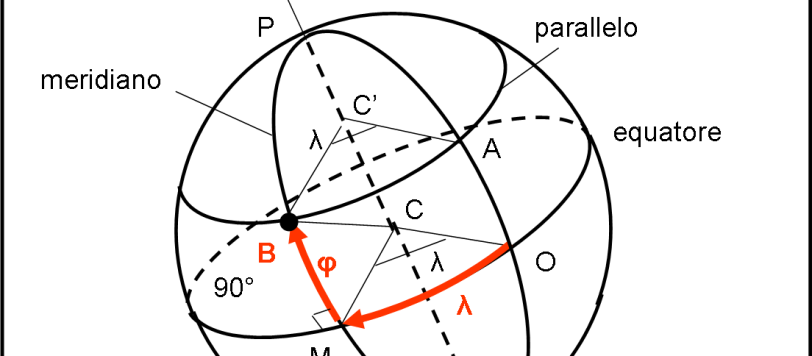
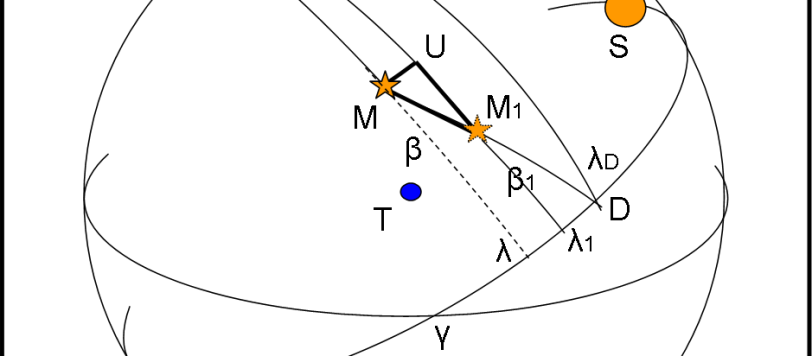
Capisco benissimo che le coordinate sferiche siano una cosa abbastanza “noiosa” e appaiano poco importanti per comprendere i misteri del Cosmo. Tuttavia, esse sono di fondamentale importanza per eseguire calcoli e trasformazioni tra le posizioni apparenti degli astri. E’ un po’ come se volessimo scrivere un grande romanzo, ma considerassimo inutile o quasi imparare l’alfabeto… Per cui vado avanti, comunque, e lascio un quiz per tutti coloro che amano la trigonometria e vogliano capire sempre meglio come si possa lavorare su una superficie sferica. Ricordiamoci che la superficie sferica -e le sue regole- sono la base della Relatività Generale… Concludiamo la nostra trattazione con il quarto sistema di coordinate celesti, particolarmente usato per le posizioni dei corpi celesti “vagabondi”.