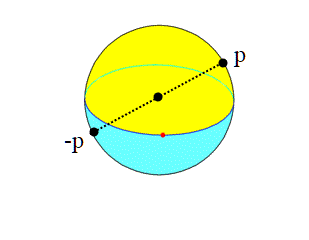
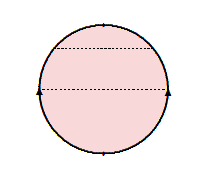
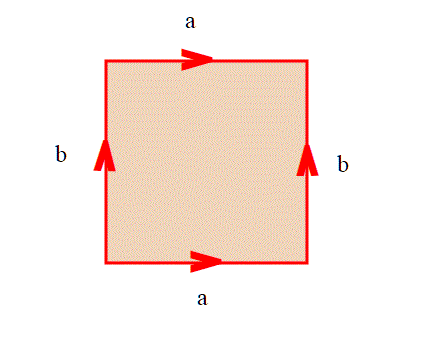
Grazie alla topologia quoziente saremo in grado di costruire degli spazi topologici nuovi e molto interessanti, tipo appunto il nastro di Möbius. Si, siamo arrivati al dunque, ma ancora un attimo di pazienza. Le costruzioni che faremo ci faranno capire l'importanza in matematica delle relazioni di equivalenza, con le quali è possibile perfino "incollare" dei punti di uno spazio topologico.