Mi piace leggere di fisica e scienze fin dalle prime letture. Questa passione mi ha orientato verso studi tecnico-scientifici, portandomi alla laurea in ingegneria. Il lavoro ed altri interessi avevano attenuato la mia frequentazione dei testi scientifici. Qualche anno fa, con l'arrivo dei primi capelli bianchi, mi è tornata la voglia di conoscere questo universo del quale faccio parte. Sarà forse stato il senso del tempo che trascorre inesorabilmente. Ai testi divulgativi ho cercato di affiancare anche lo studio di materiale più impegnativo. Lo sviluppo del Web è stato essenziale mettendo a disposizione informazioni praticamente impossibili da reperire in altro modo per un autodidatta. Sul Web ho incontrato questo circolo nel quale ho trovato l'approccio alla divulgazione che cercavo. Confesso, senza pentimento però, di avere passato parecchie notti estive armeggiando intorno ad un telescopio. D'accordo non c'è nulla di scientifico, però pensare che quei fotoni che colpiscono la mia retina o il sensore della mia macchina vengono direttamente da quegli oggetti così lontani ed interessanti mi emoziona.
In questo articolo iniziamo ad esplorare come la teoria standard interpreta i fatti che abbiamo visto nei due articoli precedenti. Vedremo come è rappresentato lo stato quantistico di un fotone con la sua polarizzazione e come questo stato evolve al passaggio in un cristallo polarizzatore. Passeremo poi alla descrizione di come il vettore di stato si modifica nel processo di misura (riduzione o collasso del vettore di stato).
Proseguo con le descrizione di alcuni fatti sperimentali. L'obiettivo è arrivare alla relazione che lega la polarizzazione dei fotoni entranti in un cristallo polarizzatore con le frazioni di fotoni rivelati dai due contatori all'uscita del cristallo. La relazione è nota come legge di Malus. In appendice c'è anche una breve introduzione ai vettori.
Riprendo il discorso sulla disuguaglianza di Bell. In questo articolo iniziamo il percorso esaminando alcuni fatti riguardanti la polarizzazione dei fotoni. Questi fenomeni, noti fin da inizio 1800, hanno una interpretazione quantistica che ci permetterà di avvicinarci negli articoli successivi ad alcuni degli elementi che sono alla base della Interpretazione Standard. Inoltre alcune delle possibili disuguaglianze di Bell riguardano proprio un particolare fenomeno di polarizzazione di coppie di fotoni. È in base a queste disuguaglianze che sono stati condotti la maggior parte degli esperimenti, tra i quali quelli condotti da Alain Aspect, che hanno messo alla prova le interpretazioni locali della meccanica quantistica.
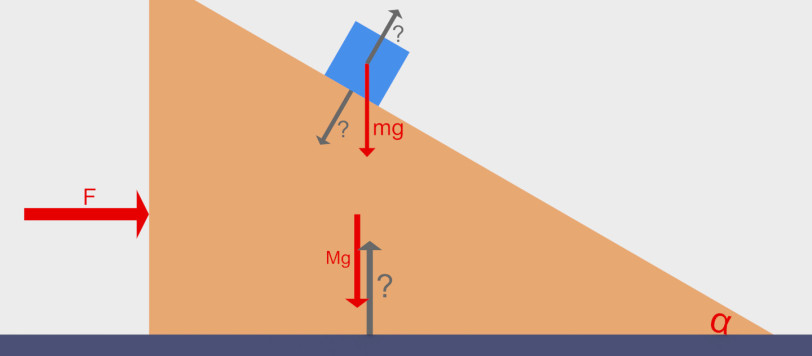
Questo articolo fa parte di una piccola serie dedicata ad un approfondimento sui metodi di soluzione del quiz sul cubo ed il cuneo proposto da Enzo. Questo articolo è dedicato all’applicazione del metodo di Lagrange. L’articolo dovrebbe essere accessibile anche a chi non conosce questo metodo. Per questo accompagno l’applicazione del metodo con una sua breve descrizione.Chi ha avuto la pazienza di leggere la serie di articoli sulla Lagrangiana, potrà trovare qui una applicazione del metodo ad un caso interessante con un riepilogo ed una integrazione degli argomenti trattati negli articoli.
In particolare, questa parte è dedicata all’applicazione del metodo di Lagrange. L’articolo dovrebbe essere accessibile anche a chi non conosce questo metodo. Per questo accompagno l’applicazione del metodo con una sua breve descrizione.
Chi ha avuto la pazienza di leggere la mia serie di articoli sulla Lagrangiana, potrà trovare qui una applicazione del metodo ad un caso interessante con un riepilogo ed una integrazione degli argomenti trattati negli articoli.
Niels Bohr disse una volta ad Einstein ".. non tocca a noi dire a Dio come deve far andare il mondo". Certo, Einstein sembra essere stato un consigliere ascoltato su come devono andare le cose su scala macroscopica. Ma quando andiamo su scala microscopica, sembra ormai certo che la Natura non lo abbia voluto ascoltare.
In questo articolo vedremo in che modo si è arrivati a questa conclusione. Il contributo principale è stato dato da John Stewart Bell nel 1964 con la disuguaglianza che ora porta il suo nome, la disuguaglianza di Bell. In base alla disuguaglianza di Bell sono stati concepiti alcuni esperimenti, tra i quali quelli condotti da Alain Aspect, che hanno permesso di identificare il comportamento della Natura riguardo le ipotesi di Einstein.
Seguendo gli articoli di Enzo ho notato che citava l'utilizzo della "lagrangiana", per la soluzione di un problema relativo ai punti lagrangiani. Avevo già visto citato questo misterioso oggetto anche da altri che ne parlavano come di una cosa fondamentale nella fisica classica e, ancora di più, nella fisica moderna. A grandi linee sapevo di cosa si trattasse, ma non avevo mai approfondito l'argomento. La citazione di Enzo mi ha incuriosito ulteriormente e ho cercato di capire meglio cosa fosse questa lagrangiana. Questo articolo raccoglie tutti i capitoli usciti a puntate ed è stato inserito negli approfondimenti.
Nelle precedenti puntate abbiamo fatto conoscenza con alcuni esempi di lagrangiana e visto all'opera l'equazione di Eulero-Lagrange su uno di questi esempi. Ora abbiamo tutti gli elementi per tornare al punto di partenza. La frase di Enzo nell'articolo sui punti lagrangiani che mi aveva inizialmente incuriosito: "Per calcolarne l'energia potenziale sarebbe più "fine" usare la Lagrangiana". Ma prima dovremo passare per un esempio di applicazione del metodo di Lagrange ad un sistema non inerziale che finora non abbiamo visto. Ci farà incontrare una vecchia amica che ci inizierà a svelare la frase di Enzo.
Fabricius usa la pietra Lagrangiana per risolvere i problemi. Con la parola magica KappaU li chiude nella pietra che colpita dalla luce Eulgrange emette la soluzione. Noi ci dobbiamo accontentare del metodo di Lagrange che attraverso l'energia cinetica (K) e l'energia potenziale (U) ci fa costruire la lagrangiana. La lagrangiana elaborata con l'equazione di Eulero-Lagrange ci fornisce la soluzione.
Nelle puntate precedenti abbiamo costruito alcuni esempi di lagrangiane di corpi liberi e vincolati ed abbiamo preso confidenza con le derivate che sono utilizzate nella equazione di Eulero-Lagrange.
In questa quinta parte dell'articolo finalmente arriviamo alla equazione di Eulero-Lagrange.
Il viaggio verso l'equazione di Eulero-Lagrange continua.
Occorre fare ancora una tappa per completare la conoscenza delle derivate utilizzate nella equazione.
Come nei gruppi ben affiatati che affrontano i sentieri di montagna, procediamo ad un passo che spero possa permettere a tutti di godere del percorso.
L'equazione di Eulero-Lagrange richiede che siano fatte alcune derivate della lagrangiana.
A prima vista queste derivate hanno un aspetto che potrebbe intimorire, ma dietro l'apparenza non c'è niente di particolarmente difficile rispetto a quelle viste negli articoli di Enzo. Occorre solo farci l'abitudine.
Per iniziare a familiarizzare con queste derivate ho pensato di proporvi questo percorso di avvicinamento alla equazione di Eulero-Lagrange. Strada facendo faremo l'abitudine ad uno degli aspetti che a me ha inizialmente confuso.
In questa terza parte proseguo a proporvi alcuni esempi di lagrangiane. Vedremo alcune lagrangiane di corpi vincolati a seguire delle traiettorie predefinite che mettono in evidenza alcune caratteristiche importanti della lagrangiana e del metodo di Lagrange. Proprio lo studio di questo tipo di problemi ha dato origine al metodo di Lagrange.
In questa seconda parte inizio a proporvi alcuni esempi con i quali ho cercato di esplorare alcune delle forme che può prendere la lagrangiana a secondo del tipo di coordinate e di riferimento che scegliamo. Questi esempi vorrebbero introdurre gradualmente quello che serve per applicare il metodo di Lagrange alla ricerca dei punti lagrangiani.