Questo articolo cosituisce un "intermezzo" necessario a fornire strumenti utili per la prosecuzione dello studio degli infiniti di Cantor
About: Umberto Cibien
Sono nato a Belluno nel 1960, dove vivo attualmente. Ho inizialmente intrapreso gli studi universitari in Informatica, per poi passare alla facoltà di matematica. Lavoro nel campo dell'informatica, come sviluppatore software in vari linguaggi di programmazione. Ma la mia vera passione resta la matematica pura. Sto cercando di divulgarla scrivendo articoli alla portata di tutti e cercando di usare il minimo formalismo. Il mio obiettivo è quello di rendere più simpatica la tanto odiata matematica che a volte ci è stata propinata come un ammasso informe di tecniche di calcolo senza alcun riferimento storico-culturale, oltre a quello di far conoscere a tutti dei concetti che sembreranno appartenere più alla filosofia che alla scienza vera e propria.
Recent Posts by Umberto Cibien
Se le infinite stanze dell'hotel "Hilbert" non sono sufficienti, ci si può trasferire da Cantor...
Affermiamo intanto che un insieme è finito se riusciamo a contare il numero dei suoi elementi. Tale numero è proprio la cardinalità dell'insieme.
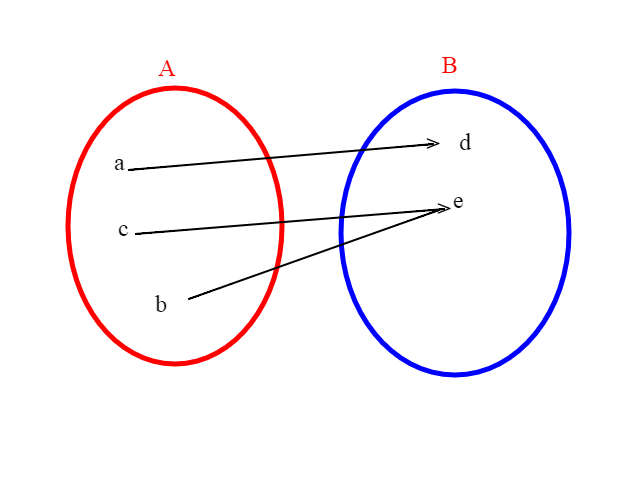
Adesso che abbiamo introdotto il concetto di insieme, vediamo come legare fra loro due insiemi.
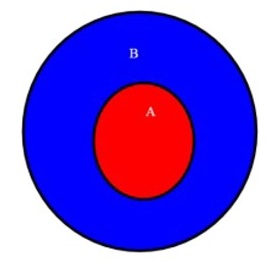
Già nell'antica Grecia era noto il concetto di infinito, Galileo aveva già compreso a quali paradossi può portare, ma la formulazione matematica rigorosa è dei tempi moderni (circa nel 1878) ed è dovuta a Georg Cantor. Il grande matematico David Hilbert disse di lui: « Nessuno riuscirà a cacciarci dal Paradiso che Cantor ha creato per noi. »
Che Riemann non scherzasse affatto con le sue innovazioni è cosa certa; non tutti però conoscono Lebesgue, che fu un personaggio forse non troppo di rilievo nella matematica recente (recente per modo di dire), ma che spianò la strada per una matematica che forse ha i più efficaci risvolti in fisica non classica.
IL quiz, che trovate qui , richiedeva di dimostrare che il sin10° è un numero irrazionale. Come detto nell'introduzione al quiz, esso era dedicato agli amanti della trigonometria, che invece io uso solo per stretta necessità. In ogni caso, ritengo che anche chi conosca appena la materia, ricordi a memoria la formula di addizione degli […]
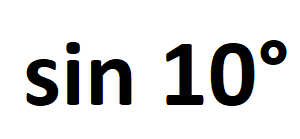
La prima volta che ho visto questo problema, a cui sinceramente non ho dato molta importanza, è stato su un sito in lingua inglese; tutti conoscono il traduttore automatico di google, che a volte parte appunto da solo e traduce in italiano. Ho pensato : ma cosa c'entra questo con la matematica? L'ho poi ritradotto […]
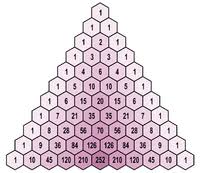
Grazie a Fabrizio e Maurizio, ci siamo liberati di un problema non proprio banale, che consisteva nel trovare il numero di cifre di una potenza: Fabrizio ha proprio fatto ciò che intendevo io, quando nel testo mi riferivo come suggerimento nascosto al binomio di Newton. Ritengo questa soluzione quella più precisa, che richiede meno approssimazioni […]
Un quiz a prima vista poco interessante, che non ha risvolti teorici o pratici .Consideriamolo come un giochetto per chi ama dilettarsi con numeri e potenze. Potrebbe essere molto utile per la soluzione l'applicazione di una formula scoperta da quello che per me è stato il più abile fisico-matematico di tutti i tempi (questa naturalmente […]
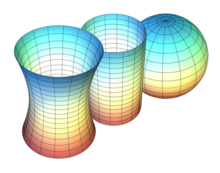
La curvatura è un argomento che è stato più volte trattato in questo circolo dal punto di visto divulgativo. Vogliamo adesso approfondire tale concetto nel caso delle superfici. Per capire a fondo il concetto di spazio curvo, dobbiamo pensare alla dimensione della varietà (in questo caso 2) e pensare come vivere in uno spazio bidimensionale come esseri piatti. Il resto viene di conseguenza.
Questa miniserie avrà un seguito, che sarà proprio la "soluzione" del paradosso. Non è un quiz, ma mi piacerebbe molto se qualcuno avesse qualcosa da dire a riguardo, sfruttando soprattutto gli articoli citati alla fine del presente articolo.
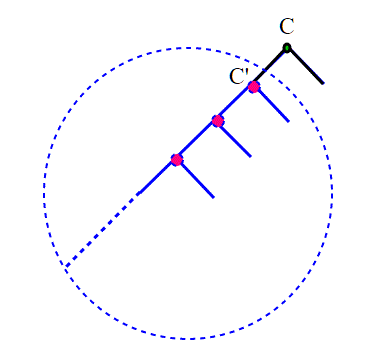
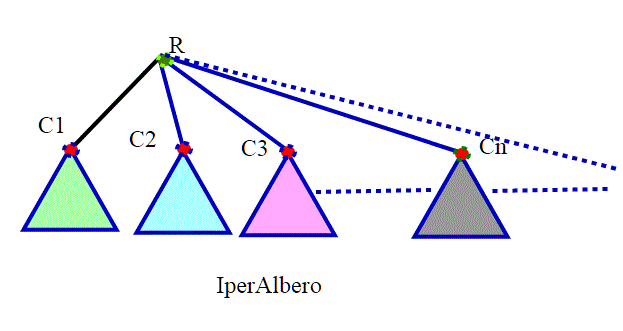
Ormai stiamo spaziando da un argomento all'altro della matematica, anche con piccoli concetti che, pur essendo intuitivi, forse non hanno mai avuto nella nostra esperienza matematica una precisa collocazione. Chiariamo bene prima il concetto di albero, per affrontare poi un simpatico paradosso che può essere denominato come la versione geometrica dell ultra famoso paradosso di […]
Un problema tipico di Ramsey, anche se la teoria sviluppata dal grande matematico, non è atta a risolvere in dettaglio ogni tipologia di questi problemi. Spesso e volentieri bisogna arrangiarsi con un po' di fantasia.
Per chi ha necessità di scrivere formule matematiche con latex (anche nei commenti): l'fx di latex della barra degli strumenti non si apre più nè nell'editor degli articoli, nè nell'editor commenti Questo link per ora sembra funzionare https://www.codecogs.com/latex/eqneditor.php Sia per chi agisce nell'editor che nei commenti basta selezionare in 1) la formula e copiarla e […]
In questo articolo vedremo come trasportare concetti applicati ai vettori ordinari di R^n , quali norma (lunghezza) prodotto scalare, trasformazioni lineari, matrici , scomposizioni tramite una base, le proiezioni su tale base (e un concetto nuovo, che vedremo in seguito, gli autovalori e non dimentichiamoci di Pitagora!) ad uno spazio in cui i vettori non […]